Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft

Faktorielle ANOVA 1: balancierte Designs, keine Wechselwirkungen

Als wir in Kapitel Vergleich mehrerer Mittelwerte (einfaktorielle ANOVA) die Varianzanalyse eingeführt haben, sind wir von einem recht einfachen Versuchsplan ausgegangen. Jede Person gehört zu einer von mehreren Gruppen, und wir wollen wissen, ob diese Gruppen unterschiedliche Mittelwerte für eine Ergebnisvariable aufweisen. In diesem Abschnitt werde ich eine breitere Klasse von Versuchsplänen erörtern, die als faktorielle Versuchspläne bekannt sind und in denen es mehr als eine Gruppierungsvariable gibt. Ich habe oben ein Beispiel für diese Art von Versuchsplan gegeben. Ein weiteres Beispiel findet sich in Kapitel Vergleich mehrerer Mittelwerte (einfaktorielle ANOVA), wo wir die Wirkung verschiedener Medikamente auf die Stimmungsänderung (mood.gain) verschiedener Personen erfahren haben. In diesem Kapitel haben wir einen signifikanten Effekt des Medikaments gefunden, aber am Ende des Kapitels haben wir auch eine Analyse durchgeführt, um zu sehen, ob es einen Effekt der Therapie gibt. Wir haben keinen gefunden, aber es ist etwas beunruhigend, zwei getrennte Analysen durchzuführen, um dasselbe Ergebnis vorherzusagen. Vielleicht gibt es tatsächlich einen Effekt der Therapie auf die Stimmungsverbesserung, aber wir konnten ihn nicht finden, weil er durch den Effekt des Medikaments „versteckt“ wurde? Mit anderen Worten, wir wollen eine einzelne Analyse durchführen, die sowohl drug als auch therapy als Prädiktoren enthält. Für diese Analyse wird jede Person nach dem Medikament, das sie erhalten hat (ein Faktor mit 3 Stufen), und der Therapie, die sie erhalten hat (ein Faktor mit 2 Stufen), klassifiziert. Wir bezeichnen dies als 3 × 2 faktorielles Design.

Wenn wir drug und therapy kreuztabellieren, indem wir die Analyse Frequencies → Contingency Tables in jamovi verwenden (siehe Erstellen von Häufigkeitstabellen und Kreuztabellen aus Ihren Daten), erhalten wir die in Abb. 144 gezeigte Tabelle.

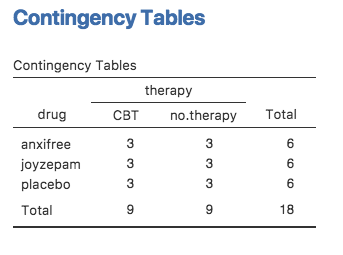
Abb. 144 jamovi-Kreuztabelle für Arzneimittel (drug) und Therapie (therapy)

Wie Sie sehen, haben wir nicht nur Teilnehmer, die allen möglichen Kombinationen der beiden Faktoren entsprechen, was darauf hindeutet, dass unser Design vollständig gekreuzt ist, sondern es stellt sich auch heraus, dass sich in jeder Gruppe auch die gleiche Anzahl von Personen befindet. Mit anderen Worten, wir haben ein balanciertes Design. In diesem Abschnitt werde ich darüber sprechen, wie man Daten aus balancierten Designs analysiert, da dies der einfachste Fall ist. Die Geschichte für unbalancierte Designs ist aufwändiger, also lassen wir sie für den Moment beiseite.

Welche Hypothesen testen wir?

Wie die einfaktorielle ANOVA ist die (mehr-)faktorielle ANOVA ein Instrument zur Prüfung von Hypothesen über die Mittelwerte einer Population. Ein sinnvoller Anfang wäre also, sich klar darüber zu werden, was eigentlich unsere Hypothesen sind. Bevor wir jedoch zu diesem Punkt kommen, ist es nützlich, eine saubere und einfache Notation zur Beschreibung der Populationsmittelwerte einzuführen. Aufgrund der Tatsache, dass die Beobachtungen in Bezug auf zwei verschiedene Faktoren klassifiziert werden, gibt es eine ganze Reihe von Mittelwerten, an denen man interessiert sein könnte. Um dies zu erkennen, sollten wir zunächst über die verschiedenen Stichprobenmittelwerte nachdenken, die wir für diese Art von Design berechnen können. Zunächst ist es naheliegend, dass wir an der folgenden Liste von Gruppenmittelwerten interessiert sind:

drug     therapy     mood.gain
placebo  no.therapy  0.300000
anxifree no.therapy  0.400000
joyzepam no.therapy  1.466667
placebo     CBT      0.600000
anxifree    CBT      1.033333
joyzepam    CBT      1.500000

Diese Ausgabe zeigt eine Liste der Gruppenmittelwerte für alle möglichen Kombinationen der beiden Faktoren (z. B. Personen, die das Placebo und keine Therapie erhielten; Personen, die das Placebo erhielten und gleichzeitig eine CBT, usw.). Es ist hilfreich, all diese Zahlen sowie die Rand- und Gesamtmittelwerte in einer einzigen Tabelle zusammenzufassen, die wie folgt aussieht:

	keine Therapie	CBT	insgesamt
placebo	0.30	0.60	0.45
anxifree	0.40	1.03	0.72
joyzepam	1.47	1.50	1.48
insgesamt	0.72	1.04	0.88

Jeder dieser verschiedenen Mittelwerte ist natürlich eine Stichprobenstatistik. Es ist eine Größe, die sich auf die spezifischen Beobachtungen bezieht, die wir während unserer Studie gemacht haben. Worauf wir aber Rückschlüsse ziehen wollen, sind die entsprechenden Populationsparameter. Das heißt, die wahren Mittelwerte, wie sie in einer breiteren Population existieren. Diese Populationsmittelwerte können in einer ähnlichen Tabelle dargestellt werden, aber dazu benötigen wir etwas mathematische Notation. Wie üblich werde ich das Symbol µ verwenden, um einen Populationsmittelwert zu bezeichnen. Da es jedoch viele verschiedene Mittelwerte gibt, muss ich zur Unterscheidung zwischen ihnen tiefgestellte Indizes verwenden.

Die Notation funktioniert folgendermaßen. Unsere Tabelle ist durch die zwei Faktoren definiert (bzw. determiniert). Jede Zeile entspricht einer Stufe des Faktors A (in diesem Fall drug), und jede Spalte entspricht einer Stufe des Faktors B (in diesem Fall therapy). Wenn wir die Anzahl der Zeilen in der Tabelle als R und die Anzahl der Spalten als C bezeichnen, können wir dies als eine R × C faktorielle ANOVA bezeichnen. In diesem Fall ist R = 3 und C = 2. Wir verwenden Kleinbuchstaben, um auf bestimmte Zeilen und Spalten zu verweisen, so dass µ_rc sich auf den Populationsmittelwert bezieht, der mit der r-ten Ebene von Faktor A (d.h. der Zeilennummer r) und der c-ten Ebene von Faktor B (der Spaltennummer c) verbunden ist.[1] Die Populationsmittelwerte werden nun also wie folgt gekennzeichnet:

	keine Therapie	CBT	insgesamt
placebo	µ11	µ11
anxifree	µ21	µ11
joyzepam	µ31	µ11
insgesamt

Darüber hinaus gibt es eine Reihe von weiteren Einträgen: Wir sollten zum Beispiel die durchschnittliche Stimmungsverbesserung über die gesamte (hypothetische) Population von Personen beschreiben, die Joyzepam erhalten haben, unabhängig davon, ob sie an einer CBT teilgenommen haben oder keine Therapie erhielten. Wir verwenden die „Punkt“-Notation, um dies auszudrücken. Im Fall von Joyzepam ist zu beachten, dass wir über den Mittelwert sprechen, der mit der dritten Zeile in der Tabelle verbunden ist. Das heißt, wir mitteln über zwei Zellenmittelwerte (d. h. µ₃₁ und µ₃₂). Das Ergebnis dieser Mittelwertbildung wird als Randmittel (marginal means) bezeichnet und würde in diesem Fall mit µ_3. bezeichnet werden. Das Randmittel für CBT entspricht dem Mittelwert aller Bedingungen, die mit der zweiten Spalte in der Tabelle verbunden sind, daher verwenden wir die Notation µ_.2, um ihn zu beschreiben. Der Gesamtmittelwert wird mit µ_.. bezeichnet, weil er der Mittelwert ist, der durch Mittelung (Marginalisierung[2]) von beiden erhalten wird. Unsere vollständige Tabelle der Populationsmittelwerte kann also folgendermaßen geschrieben werden:

	keine Therapie	CBT	insgesamt
placebo	µ11	µ12	µ1.
anxifree	µ21	µ22	µ2.
joyzepam	µ31	µ32	µ3.
insgesamt	µ.1	µ.2	µ..

Jetzt, da wir diese Notation haben, ist es einfach, einige Hypothesen zu formulieren und auszudrücken. Nehmen wir an, dass das Ziel darin besteht, zwei Dinge herauszufinden. Erstens: Hat die Wahl des Medikaments einen Einfluss auf die Stimmung? Und zweitens: Hat die CBT einen Einfluss auf die Stimmung? Dies sind natürlich nicht die einzigen Hypothesen, die wir formulieren könnten, aber es sind die beiden am einfachsten zu prüfenden Hypothesen, und deshalb beginnen wir damit. Wir werden danach im Abschnitt Faktorielle ANOVA 2: balancierte Designs mit Wechselwirkungen näher auf ein Beispiel für eine andere, komplexere Art von Hypothese eingehen. Betrachten wir den ersten Test. Wenn das Medikament keine Wirkung hat, dann würden wir erwarten, dass alle Zeilenmittelwerte identisch sind, richtig? Das ist also unsere Nullhypothese. Wenn das Medikament jedoch eine Rolle spielt, dann sollten wir erwarten, dass die Mittelwerte der Zeilen unterschiedlich sind. Formal schreiben wir unsere Null- und Alternativhypothese in Form der Gleichheit der Randmittel auf:

Nullhypothese, H0:	Die Zeilenmittelwerte sind gleich, d. h. µ1. = µ2. = µ3.
Alternativhypothese, H1:	Mindestens ein Zeilenmittelwert ist unterschiedlich.

Es ist erwähnenswert, dass dies dieselben statistischen Hypothesen sind, die wir für die einfaktorielle ANOVA mit diesen Daten im vorigen Kapitel benutzt haben. Damals verwendete ich die Schreibweise µ_P für den mittleren Stimmungszuwachs der Placebogruppe, wobei µ_A und µ_J den Gruppenmittelwerten für die beiden Medikamente entsprachen, und die Nullhypothese lautete µ_P = µ_A = µ_J. Wir sprechen also eigentlich über dieselbe Hypothese, es ist nur so, dass die kompliziertere ANOVA aufgrund des Vorhandenseins mehrerer gruppierender Variablen eine sorgfältigere Schreibweise erfordert, so dass wir uns jetzt auf diese Hypothese als µ_1. = µ_2. = µ_3. beziehen. Wie wir jedoch gleich sehen werden, ist der Test dieser Hypothese, obwohl die Hypothese identisch ist, aufgrund der Tatsache, dass wir nun die Existenz der zweiten gruppierenden Variablen anerkennen, etwas anders.

Was die andere Gruppierungsvariable betrifft, so wird es Sie nicht überraschen, dass unser zweiter Hypothesentest auf die gleiche Weise formuliert ist. Da es sich jedoch um die psychologische Therapie und nicht um die Medikamente handelt, entspricht unsere Nullhypothese nun der Gleichheit der Spaltenmittelwerte:

Nullhypothese, H0:	Die Spaltenmittelwerte sind gleich, d. h. μ:sub:‘.1‘ = μ:sub:‘.2‘
Alternativhypothese, H1:	Die Spaltenmittelwerte sind unterschiedlich, d. h. µ.1 ≠ µ.2

Durchführen der Analyse in jamovi

Die Null- und die Alternativhypothesen, die ich im letzten Abschnitt beschrieben habe, sollten Ihnen vertraut vorkommen. Sie sind im Grunde die gleichen wie die Hypothesen, die wir in unserer einfacheren einfaktoriellen ANOVA getestet haben. Sie erwarten also wahrscheinlich, dass die Hypothesentests, die in der (mehr-)faktoriellen ANOVA verwendet werden, im Wesentlichen die gleichen sind wie der F-Test aus dem vorigen Kapitel. Sie erwarten Hinweise auf Quadratsummen (SS), mittlere quadrierte Abweichungen (MS), Freiheitsgrade (df) und schließlich eine F-Statistik, die wir in einen p-Wert umwandeln können? Sie haben absolut und vollkommen Recht. So sehr, dass ich von meinem üblichen Ansatz abweichen werde. In diesem Buch habe ich im Allgemeinen zuerst die Logik (und bis zu einem gewissen Grad die Mathematik) beschrieben, die einer bestimmten Analyse zugrunde liegt, und erst danach vorgestellt, wie die Analyse in jamovi durchgeführt wird. Dieses Mal werde ich es andersherum machen und Ihnen zuerst zeigen, wie man die Analyse in jamovi durchführt. Der Grund dafür ist, dass ich die Ähnlichkeiten zwischen der einfacheren einfaktoriellen ANOVA, die wir im vorherigen Kapitel besprochen haben, und dem komplexeren Vorgehen, das wir in diesem Kapitel verwenden werden, hervorheben möchte.

Wenn die Daten, die Sie zu analysieren versuchen, einem balancierten faktoriellen Design entsprechen, ist das Durchführen Ihrer Varianzanalyse einfach. Um zu sehen, wie einfach es ist, beginnen wir mit der Reproduktion der ursprünglichen Analyse aus dem Kapitel Vergleich mehrerer Mittelwerte (einfaktorielle ANOVA). Falls Sie es vergessen haben, für diese Analyse verwendeten wir nur einen einzigen Faktor (d.h. drug), um unsere Ergebnisvariable (d.h. mood.gain) vorherzusagen, und wir erhielten die in Abb. 145 gezeigten Ergebnisse.

Abb. 145 Einfaktorielle ANOVA in jamovi bei der mood.gain durch drug vorhergesagt wird

Nehmen wir nun an, dass ich auch herausfinden möchte, ob therapy eine Beziehung zu mood.gain hat. In Anbetracht dessen, was wir in unserer Diskussion über multiple Regression in Kapitel Korrelation und lineare Regression gesehen haben, wird es Sie wahrscheinlich nicht überraschen, dass wir nur therapy als zweiten Fixed Factor in die Analyse aufnehmen müssen, wie in Abb. 146 gezeigt.

Abb. 146 Faktorielle ANOVA für mood.gain mit den Faktoren drug und therapy in jamovi

Auch diese Ausgabe ist einfach und übersichtlich. Die erste Zeile der Tabelle gibt einen Wert für die Quadratsumme (SS) an, der mit dem (Zwischensubjekt-)Faktor drug verbunden ist, zusammen mit der entsprechenden Anzahl von Freiheitsgraden (df). Es werden außerdem die mittleren quadrierten Abweichungen (MS), eine F-Statistik und ein p-Wert ausgegeben. Die zweite Zeile gibt diese Werte für den Faktor therapy aus und die dritte Zeile die Residuen (d. h. die verbleibende, unerklärte Variation innerhalb jeder Gruppe).

Nicht nur, dass alle einzelnen Größen ziemlich vertraut sind, auch die Beziehungen zwischen diesen verschiedenen Größen sind unverändert geblieben, genau wie wir es bei der ursprünglichen einfaktoriellen ANOVA gesehen haben. Beachten Sie, dass die mittleren quadrierten Abweichungen (MS) durch die Division von SS durch die entsprechenden df berechnet wird. Das heißt, es ist immer noch wahr, dass:

MS = SS / df

unabhängig davon, ob es sich um drug, therapy oder um die Residuen handelt. Wir machen uns zunächst keine Gedanken darüber, wie die Summen der Quadrate berechnet werden. Stattdessen nehmen wir an, dass jamovi die SS-Werte korrekt berechnet hat, und versuchen zu überprüfen, ob alle anderen Zahlen Sinn ergeben. Beachten Sie zunächst, dass wir für den Faktor drug 3,45 durch 2 dividieren und eine mittlere quadrierte Abweichung von 1,73 erhalten. Für den Faktor therapy gibt es nur einen Freiheitsgrad, so dass unsere Berechnungen noch einfacher sind: wenn wir 0,47 (den SS-Wert) durch 1 teilen, erhalten wir 0,47 (den MS-Wert).

Bei der Betrachtung der F-Statistik und der p-Werte fällt auf, dass es jeweils zwei davon gibt; eine für den Faktor drug und die andere für den Faktor therapy. Unabhängig davon, um welchen Faktor es sich handelt, wird die F-Statistik berechnet, indem die mittleren quadrierten Abweichungen des Faktors durch die mittleren quadrierten Abweichungen der Residuen geteilt werden. Wenn wir „A“ als Kurzschreibweise für den ersten Faktor (Faktor A; in diesem Fall drug) und „R“ als Kurzschreibweise für die Residuen verwenden, dann wird die F-Statistik, die dem Faktor A zugeordnet ist, mit F_A bezeichnet und wie folgt berechnet:

F_A = MS_A / MS_R

und eine äquivalente Formel existiert für den Faktor B (d.h. therapy). Beachten Sie, dass die Verwendung von „R“ für Residuen etwas unglücklich ist, da wir den Buchstaben R auch für die Anzahl der Zeilen in der Tabelle verwendet haben, aber ich werde „R“ nur für Residuen im Zusammenhang mit SS_R und MS_R verwenden, so dass dies hoffentlich nicht verwirrend sein sollte. Wie auch immer, um diese Formel auf den Faktor drug anzuwenden, nehmen wir die mittlere quadrierte Abweichung von 1,73 und teilen sie durch die mittlere quadrierte Abweichung der Residuen von 0,07, was uns eine F-Statistik von 26,15 ergibt. Die entsprechende Berechnung für den Faktor therapy wäre, 0,47 durch 0,07 zu teilen, was 7,08 als F-Statistik ergibt. Es überrascht nicht, dass dies die gleichen Werte sind, die jamovi in der ANOVA-Tabelle oben angegeben hat.

In der ANOVA-Tabelle ist auch die Berechnung der p-Werte enthalten. Auch hier gibt es nichts Neues. Für jeden unserer beiden Faktoren versuchen wir, die Nullhypothese zu testen, dass es keinen Zusammenhang zwischen dem Faktor und der Ergebnisvariablen gibt (ich werde das später noch etwas genauer erläutern). Zu diesem Zweck haben wir (offenbar) eine ähnliche Strategie wie bei der einfaktoriellen ANOVA verfolgt und für jede dieser Hypothesen eine F-Statistik berechnet. Um diese in p-Werte umzuwandeln, müssen wir nur beachten, dass die Stichprobenverteilung für die F-Statistik unter der Nullhypothese (dass der betreffende Faktor irrelevant ist) eine F-Verteilung ist. Beachten Sie auch, dass die beiden Werte der Freiheitsgrade diejenigen sind, die dem Faktor und den Residuen entsprechen. Für den Faktor drug handelt es sich um eine F-Verteilung mit 2 und 14 Freiheitsgraden (auf die Freiheitsgrade gehe ich später noch genauer ein). Im Gegensatz dazu ist die Stichprobenverteilung für den Faktor therapy eine F-Verteilung mit 1 und 14 Freiheitsgraden.

An dieser Stelle können Sie hoffentlich erkennen, dass die ANOVA-Tabelle für diese komplexere mehrfaktorielle Analyse ähnlich zu lesen ist wie die ANOVA-Tabelle für die einfachere einfaktorielle Analyse. Kurz gesagt, sie sagt uns, dass die faktorielle ANOVA für unser 3 × 2 Design einen signifikanten Effekt des Medikaments gefunden hat: F(2,14) = 26.15, p < 0.001, sowie einen signifikanten Effekt der Therapie: F(1,14) = 7,08, p = 0,02. Oder, um die technisch korrekte Terminologie zu verwenden, würden wir sagen, dass es zwei Haupteffekte von Medikament und Therapie gibt. Im Moment scheint es vielleicht etwas überflüssig, von „Haupteffekten“ zu sprechen, aber es macht tatsächlich Sinn. Später werden wir über die Möglichkeit von „Wechselwirkungen“ zwischen den beiden Faktoren sprechen wollen, und daher unterscheiden wir im Allgemeinen zwischen Haupteffekten und Interaktionseffekten.

Wie berechnet man die Quadratsummen?

Im vorigen Abschnitt habe ich zwei Ziele verfolgt. Erstens wollte ich Ihnen zeigen, dass die jamovi-Methode, die für eine (mehr-)faktorielle ANOVA benutzt wird, annähernd die gleiche ist wie die, die wir für eine einfaktorielle ANOVA verwendet haben. Der einzige Unterschied besteht darin, dass ein zweiter Faktor hinzugefügt wird. Zweitens wollte ich zeigen, wie die ANOVA-Tabelle in diesem Fall aussieht, damit Sie von vornherein erkennen können, dass die grundlegende Logik und Struktur der faktoriellen ANOVA dieselbe ist wie die der einfaktoriellen ANOVA. Versuchen Sie, sich dieses Gefühl zu bewahren. Es ist wirklich wahr, denn die faktorielle ANOVA ist mehr oder weniger genauso aufgebaut wie das einfachere Modell der einfaktoriellen ANOVA. Es ist nur so, dass sich dieses Gefühl der Vertrautheit verflüchtigt, sobald man anfängt, sich in die Details zu vertiefen. Oft wird dieses beruhigende Gefühl durch den Drang ersetzt, auf die Autoren von Statistik-Lehrbüchern zu schimpfen.

Beschäftigen wir uns mit einigen dieser Details: Die Erklärung, die ich im letzten Abschnitt gegeben habe, veranschaulicht die Tatsache, dass die Hypothesentests für die Haupteffekte (von drug und therapy in diesem Fall) F-Tests sind. Was sie nicht tut, ist Ihnen zu zeigen, wie die Summe der Quadrate (SS) Werte berechnet werden. Es wird auch nicht explizit erklärt, wie man die Freiheitsgrade berechnet (df Werte), obwohl das im Vergleich eine einfache Sache ist. Wenn wir Y verwenden, um uns auf die Ergebnisvariable zu beziehen, dann würden wir Y_rci verwenden, um uns auf das Ergebnis zu beziehen, das mit dem i-ten Mitglied der Gruppe rc assoziiert ist (d.h. Zeile / Stufe r für Faktor A und Spalte / Stufe c für Faktor B). Wenn wir also Ȳ für einen Stichprobenmittelwert verwenden, können wir die gleiche Notation wie zuvor für Gruppenmittelwerte, Randmittel und Gesamtmittelwerte verwenden. Das heißt, Ȳ_rc ist der Stichprobenmittelwert, der mit der r-ten Stufe des Faktors A und der c-ten Stufe des Faktors B verbunden ist, Ȳ_r. wäre das Randmittel für die r-te Stufe von Faktor A, Ȳ_.c wäre das Randmittel für die c-te Stufe von Faktor B, und Ȳ_.. ist der Gesamtmittelwert. Mit anderen Worten, unsere Stichprobenmittelwerte können in dieselbe Tabelle eingeordnet werden wie die Mittelwerte in der Grundgesamtheit. Für unseren clinicaltrial-Datensatz sieht diese Tabelle wie folgt aus:

	keine Therapie	CBT	insgesamt
placebo	Ȳ11	Ȳ12	Ȳ1.
anxifree	Ȳ21	Ȳ22	Ȳ2.
joyzepam	Ȳ31	Ȳ32	Ȳ3.
insgesamt	Ȳ.1	Ȳ.2	Ȳ..

Wenn wir uns die Stichprobenmittelwerte ansehen, die ich vorhin gezeigt habe, haben wir Ȳ₁₁ = 0,30, Ȳ₁₂ = 0,60 usw. In unserem clinicaltrial-Datensatz hat der Faktor drug 3 Stufen und der Faktor therapy 2 Stufen, so dass wir versuchen, eine 3 × 2 faktorielle ANOVA durchzuführen. Wir werden jedoch etwas allgemeiner sein und sagen, dass der Faktor A (der Zeilenfaktor) R Stufen und der Faktor B (der Spaltenfaktor) C Stufen hat, so dass wir hier eine R × C faktorielle ANOVA durchführen.

Nachdem wir unsere Notation geklärt haben, können wir die Quadratsumme für jeden der beiden Faktoren auf die gewohnte Weise berechnen. Für Faktor A wird die Quadratsumme zwischen den Gruppen berechnet, indem das Ausmaß bewertet wird, in dem die (Zeilen-)Randmittel Ȳ_1., Ȳ_2. usw. vom Gesamtmittelwert Ȳ_..abweichen. Wir tun dies auf die gleiche Weise wie bei der einfaktoriellen ANOVA: Wir berechnen die Summe der quadrierten Abweichungen zwischen den Ȳ_i.-Werten und den Ȳ_..-Werten. Konkret berechnen wir Folgendes, wenn es N Personen in jeder Gruppe gibt

\[\mbox{SS}_{A} = (N \times C) \sum_{r=1}^R \left( \bar{Y}_{r.} - \bar{Y}_{..} \right)^2\]

Wie bei der einfaktoriellen ANOVA ist der interessanteste Teil[3] dieser Formel der (Ȳ_r. - Ȳ_..)²-Teil, das der quadratischen Abweichung entspricht, die mit der Stufe r verbunden ist. Alles, was diese Formel tut, ist, diese quadratische Abweichung für alle R Stufen des Faktors zu berechnen, sie zu addieren und dann das Ergebnis mit N × C zu multiplizieren. Der Grund für diesen letzten Teil ist, dass es in unserem Entwurf mehrere Zellen gibt, welche die Stufe r auf Faktor A haben. Tatsächlich gibt es C davon, eine entsprechend jeder möglichen Stufe des Faktors B! In unserem Beispiel gibt es zwei verschiedene Zellen im Versuchsdesign, die der Droge anxifree entsprechen: eine für die Gruppe mit no.therapy und eine für die Gruppe mit CBT. Und nicht nur das: Innerhalb jeder dieser Zellen gibt es N Beobachtungen. Wenn wir also unseren SS-Wert in eine Größe umwandeln wollen, welche die Quadratsumme zwischen den Gruppen auf einer „pro Beobachtung“-Basis berechnet, müssen wir mit N × C multiplizieren.

\[\mbox{SS}_{B} = (N \times R) \sum_{c=1}^C \left( \bar{Y}_{.c} - \bar{Y}_{..} \right)^2\]

Da wir diese Formeln haben, können wir sie mit der jamovi-Ausgabe aus dem vorherigen Abschnitt vergleichen.

Berechnen wir zunächst die Quadratesumme, die mit dem Haupteffekt von drug verbunden ist. Es gibt insgesamt N = 3 Personen in jeder Gruppe und C = 2 verschiedene Arten von Therapien. Oder anders ausgedrückt, es gibt 3 · 2 = 6 Personen, die ein bestimmtes Medikament erhalten haben. Wenn wir diese Berechnungen in einem Tabellenkalkulationsprogramm durchführen, erhalten wir einen Wert von 3,45 für die mit dem Haupteffekt von drug verbundene Quadratsumme. Es überrascht nicht, dass dies die gleiche Zahl ist, die man als SS-Wert für den Faktor drug in der ANOVA-Tabelle erhält, die in Abb. 146 dargestellt ist.

Wir können auf die gleiche Art die Berechnung für die Wirkung von therapy durchführen. Auch hier gibt es N = 3 Personen in jeder Gruppe, aber da es R = 3 verschiedene Werte in drug gibt, stellen wir dieses Mal fest, dass es 3 · 3 = 9 Personen gibt, die CBT erhalten haben und weitere 9 Personen, die no.therapy erhalten haben. Unsere Berechnung ergibt also in diesem Fall einen Wert von 0,47 für die Quadratesumme, die mit dem Haupteffekt von therapy verbunden ist. Auch hier sind wir nicht überrascht, dass unsere Berechnungen identisch mit der ANOVA-Ausgabe in Abb. 146 sind.

So berechnen Sie also die SS-Werte für die beiden Haupteffekte. Diese SS-Werte sind analog zu den Quadratsummen zwischen den Gruppen, die wir für die einfaktorielle ANOVA im vorherigen Kapitel berechnet haben. Es ist jedoch nicht ratsam, sie weiterhin als SS-Werte zwischen den Gruppen zu betrachten, da wir nun zwei unterschiedliche Gruppierungsvariablen haben und es daher leicht zu Verwechslungen kommen kann. Um einen F-Test zu konstruieren, müssen wir jedoch auch die Quadratsumme innerhalb der Gruppen berechnen. In Anlehnung an die Terminologie, die wir in Kapitel Korrelation und lineare Regression verwendet haben, und an die Terminologie, die jamovi beim Ausdrucken der ANOVA-Tabelle verwendet, werde ich den SS-Wert innerhalb der Gruppen als Quadratsumme der Residuen SS_R bezeichnen.

Am einfachsten lassen sich die SS-Werte für die Residuen in diesem Zusammenhang als die verbleibende Variation in der Ergebnisvariablen betrachten, nachdem man die Unterschiede in den Randmitteln berücksichtigt hat (d. h. nachdem man SS_A und SS_B subtrahiert hat). Was ich damit meine, ist, dass wir mit der Berechnung der Gesamt-Quadratsumme beginnen können, die ich als SS_T bezeichnen werde. Die Formel hierfür ist ziemlich genau dieselbe wie bei der einfaktoriellen ANOVA. Wir nehmen die Differenz zwischen jeder Beobachtung Y_rci und dem Gesamtmittelwert Ȳ_.., quadrieren die Differenzen und addieren sie zusammen

\[\mbox{SS}_T = \sum_{r=1}^R \sum_{c=1}^C \sum_{i=1}^N \left( Y_{rci} - \bar{Y}_{..}\right)^2\]

Die „dreifache Summierung“ sieht hier komplizierter aus, als sie ist. In den ersten beiden Summierungen summieren wir über alle Stufen von Faktor A (d. h. über alle möglichen Zeilen r in unserer Tabelle) und über alle Stufen von Faktor B (d. h. über alle möglichen Spalten c). Jede rc-Kombination entspricht einer einzelnen Gruppe, und jede Gruppe enthält N Personen, so dass wir auch über alle diese Personen (d. h. alle i-Werte) summieren müssen. Mit anderen Worten, alles, was wir hier tun, ist, über alle Beobachtungen im Datensatz zu summieren (d. h. alle möglichen rci-Kombinationen).

Zu diesem Zeitpunkt kennen wir die Gesamtvariabilität der Ergebnisvariablen SS_T, und wir wissen, wie viel von dieser Variabilität dem Faktor A (SS_A) und wie viel dem Faktor B (SS_B) zugeschrieben werden kann. Die Quadratsumme der Residuen ist somit definiert als die Variabilität in Y, die keinem unserer beiden Faktoren zugeschrieben werden kann. Mit anderen Worten

SS_R = SS_T - (SS_A + SS_B)

Natürlich gibt es auch eine Formel, mit der Sie die SS der Residuen direkt berechnen können, aber ich denke, dass es konzeptionell sinnvoller ist, wie beschrieben vorzugehen. Die Bezeichnung „Residuum“ (bzw. „Residuen“) verdeutlicht, dass es sich um die verbleibende Variation handelt, und die obige Formel macht dies deutlich. Ich sollte auch anmerken, dass es in Übereinstimmung mit der im Kapitel über Regression verwendeten Terminologie üblich ist, sich auf SS_A + SS_B als die dem „ANOVA-Modell“ zuzuschreibende Varianz zu beziehen. Diese wird mit SS_M bezeichnet, und so sagen wir oft, dass die Gesamt-Quadratsumme gleich der Modell-Quadratsumme plus der Quadratsumme der Residuen ist. Im weiteren Verlauf dieses Kapitels werden wir sehen, dass dies nicht nur eine oberflächliche Ähnlichkeit ist: ANOVA und Regression sind mathematisch eigentlich dasselbe.

In jedem Fall lohnt es sich, zu überprüfen, ob die SS_R, die wir mit dieser Formel berechnen, mit der Ausgabe übereinstimmt, die jamovi in seiner ANOVA-Tabelle liefert. Die Berechnungen sind ziemlich einfach, wenn man die jamovi benutzt, um die Variablen zu berechnen. Wir öffnen den Datensatz clinicaltrial und definieren drei berechnete Variablen (New Computed Variable unter Data): (1) sq_res_T mit (mood.gain - VMEAN(mood.gain)) ^ 2 als Formel, (2) sq_res_A mit (VMEAN(mood.gain) - VMEAN(mood.gain, group_by = drug)) ^ 2 als Formel und (3) sq_res_B mit (VMEAN(mood.gain) - VMEAN(mood.gain, group_by = therapy)) ^ 2 als Formel. Nachdem wir diese drei Variablen erstellt haben, berechnen wir die Quadratsumme mit Descriptives → Descriptive Statistics: Wir verschieben dann sq_res_T, sq_res_A und sq_res_B in das Feld Variables und wählen schließlich Sum aus dem Dropdown-Menü Statistics. SS_T (sq_res_T) hat einen Wert von 4.845, SS_A (sq_res_A) einen Wert von 3.453, und SS_B (sq_res_B) einen Wert von 0.467. Anhand dieser drei Werte können wir SS_R mit der obigen Formel berechnen.

SS_R = 4.845 - (3.453 + 0.467)

SS_R = 0.924

Alternativ dazu können wir eine weitere berechnete Variable mit dem Namen SS_R und der Formel VSUM(sq_res_T) - (VSUM(sq_res_A) + VSUM(sq_res_B)) erstellen.

Was sind unsere Freiheitsgrade?

Die Freiheitsgrade werden in ähnlicher Weise wie bei der einfaktoriellen ANOVA bestimmt. Für jeden gegebenen Faktor sind die Freiheitsgrade gleich der Anzahl der Stufen minus 1 (d. h. R - 1 für die Zeilenvariable Faktor A und C - 1 für die Spaltenvariable Faktor B). Für den Faktor drug erhalten wir also df = 2, und für den Faktor therapy erhalten wir df = 1. Später, wenn wir die Interpretation der ANOVA als Regressionsmodell erörtern (siehe Abschnitt Die ANOVA als lineares Modell), werde ich genauer erklären, wie wir zu dieser Zahl kommen. Aber im Moment können wir die einfache Definition von Freiheitsgraden verwenden, nämlich dass die Freiheitsgrade gleich der Anzahl der beobachteten Größen minus der Anzahl der Einschränkungen (constraints) sind. Für den Faktor drug beobachten wir also 3 getrennte Gruppenmittelwerte, die jedoch durch einen Gesamtmittelwert eingeschränkt werden, so dass die Freiheitsgrade 2 betragen. Für die Residuen ist die Logik ähnlich, aber nicht ganz dieselbe. Die Gesamtzahl der Beobachtungen in unserem Experiment beträgt 18. Die Einschränkungen entsprechen dem Gesamtmittelwert, den zwei zusätzlichen Gruppenmittelwerten, die der Faktor drug einführt, und dem einen zusätzlichen Gruppenmittelwert, den der Faktor therapy einführt, so dass unsere Freiheitsgrade 14 sind. In der Formel ist dies N - 1 - (R - 1) - (C - 1), was sich zu N - R - C + 1 vereinfacht.

Mit Hilfe der Freiheitsgrade und der Quadratsummen, die wir oben berechnet haben, können wir die folgenden F-Werte für die Faktoren A und B berechnen.

F_A = (SS_A / SS_A) / (SS_R / SS_R)

F_A = (3.453 / 2) / (0.924 / 14)

F_A = 1.727 / 0.066

F_A = 26.149

F_B = (SS_B / SS_B) / (SS_R / SS_R)

F_B = (0.467 / 1) / (0.924 / 14)

F_B = 0.467 / 0.066

F_B = 7.076

Auch hier können wir zwei neue berechnete Variablen erstellen, die erste mit dem Namen F_A und der Formel (VSUM(sq_res_A) / 2) / (SS_R / 14), und die zweite mit dem Namen F_B und der Formel (VSUM(sq_res_B) / 1) / (SS_R / 14).

Wer die in den vorangegangenen Abschnitten beschriebenen Berechnungen nicht selbst ausprobieren und nachvollziehen möchte, kann den Datensatz clinicaltrial_factorialanova herunterladen und öffnen und sich die Berechnungen dort ansehen.

Faktorielle ANOVA vs. einfaktorielle ANOVAs

Nachdem wir nun gesehen haben, wie eine (mehr-)faktorielle ANOVA funktioniert, lohnt es sich, sie mit den Ergebnissen der einfaktoriellen Analysen zu vergleichen. Dadurch erhalten wir einen guten Eindruck, warum es eine gute Idee ist, faktorielle ANOVAs durchzuführen. In Kapitel Vergleich mehrerer Mittelwerte (einfaktorielle ANOVA) habe ich eine einfaktorielle ANOVA durchgeführt, um zu sehen, ob es Unterschiede zwischen den drei Ebenen von drug gibt, und eine zweite einfaktorielle ANOVA, um zu sehen, ob es Unterschiede zwischen den beiden Ebenen von therapy gibt. Wie wir in Abschnitt Welche Hypothesen testen wir? gesehen haben, sind die Nullhypothese und die Alternativhypothese, die durch die einfaktoriellen ANOVAs getestet werden, identisch mit den Hypothesen, die in der faktoriellen ANOVA getestet werden. Wenn man sich die ANOVA-Tabellen noch genauer ansieht, stellt man fest, dass die Quadratesumme der Faktoren in den beiden Analysen identisch ist (3,453 für drug und 0,467 für therapy), ebenso wie die Freiheitsgrade (2 für drug, 1 für therapy). Aber sie ergeben nicht die gleichen Ergebnisse! Als wir die einfaktorielle ANOVA für therapy im Abschnitt Zur Beziehung von ANOVA und Student’s t-Test durchgeführt haben, fanden wir keinen signifikanten Effekt (der p-Wert war 0,210). Wenn wir jedoch den Haupteffekt von therapy im Rahmen der zweifaktoriellen ANOVA betrachten, erhalten wir einen signifikanten Effekt (p = 0,019). Die beiden Analysen sind eindeutig nicht identisch.

Warum ist das so? Die Antwort darin, zu verstehen, wie die Residuen berechnet werden. Erinnern Sie sich, dass die Grundlage jedes F-Tests ist, die Variabilität, die einem bestimmten Faktor zugeschrieben werden kann, mit der Variabilität zu vergleichen, die nicht durch das Gesamtmodell erklärt werden kann (die Residuen). Wenn Sie eine einfaktorielle ANOVA für therapy durchführen, wird der Effekt von drug ignoriert, und die ANOVA wird daher die gesamte medikamenteninduzierte Variabilität (d.h., durch drug erklärbare Variabilität) in den Residuen abladen! Dies hat zur Folge, dass die Daten verrauschter aussehen, als sie tatsächlich sind. Dadurch ist der Effekt von therapy, der in der zweifaktoriellen ANOVA korrekt als signifikant eingestuft wurde, nun nicht mehr signifikant. Wenn wir etwas ignorieren, das tatsächlich wichtig ist (z. B. den Beitrag von drug), wenn wir versuchen, den Beitrag von etwas anderem (z. B. therapy) zu bewerten, dann wird unsere Analyse verzerrt. Natürlich ist es völlig in Ordnung, Variablen zu ignorieren, die für das interessierende Phänomen wirklich irrelevant sind. Wenn wir die Farbe der Wände erfasst hätten und diese sich in einer dreifaktoriellen ANOVA als nicht signifikanter Faktor herausstellen würde, wäre es völlig in Ordnung, sie zu vernachlässigen und nur die einfachere zweifaktorielle ANOVA anzugeben, die diesen irrelevanten Faktor nicht enthält. Was Sie aber nicht tun sollten, ist Variablen wegzulassen, die möglicherweise einen Unterschied machen!

Abb. 147 Vier mögliche Ergebnisse einer 2 × 2 ANOVA, wenn keine Interaktionen vorhanden sind. Im linken oberen Feld sehen wir einen Haupteffekt von Faktor A, ohne einen Effekt von Faktor B. Das rechte obere Feld zeigt einen Haupteffekt von Faktor B, ohne einen Effekt von Faktor A. Das linke untere Feld zeigt Haupteffekte sowohl von Faktor A als auch von Faktor B. Das rechte untere Feld schließlich zeigt, wenn keiner der Faktoren einen Effekt hat.

Welche Arten von Ergebnissen erfasst diese Analyse?

Das ANOVA-Modell, über das wir bisher gesprochen haben, deckt eine Reihe von Mustern ab, die wir in unseren Daten beobachten können. Bei einem zweifaktoriellen ANOVA-Design gibt es zum Beispiel vier Möglichkeiten. Ein Beispiel für jede dieser vier Möglichkeiten ist in Abb. 147 dargestellt: (1) nur Faktor A spielt eine Rolle (oben links), (2) nur Faktor B spielt eine Rolle (oben rechts), (3) sowohl A als auch B spielen eine Rolle (unten links), und (4) weder A noch B spielen eine Rolle (unten rechts).

---

[1]

Das Schöne an der tiefgestellten Notation ist, dass sie sich sehr gut verallgemeinern lässt. Wenn in unserem Experiment ein dritter Faktor hinzugefügt würde, könnten wir einfach einen dritten tiefgestellten Wert benutzen. Im Prinzip lässt sich die Notation auf beliebig viele Faktoren ausdehnen, aber in diesem Buch werden wir selten Analysen mit mehr als zwei und nie mehr als drei Faktoren betrachten.

[2]

Technisch gesehen ist die Marginalisierung (das Berechnen von Randmitteln) nicht ganz identisch mit einem normalen Mittelwert. Es handelt sich um einen gewichteten Mittelwert, bei dem die Häufigkeit der verschiedenen Ereignisse berücksichtigt wird, über die der Mittelwert gebildet wird. In einem balancierten Design sind jedoch alle Zellhäufigkeiten per Definition gleich, so dass die beiden Resultate gleichwertig sind. Wir werden uns später mit unbalancierten Designs befassen, und dann werden Sie sehen, dass unsere Berechnungen schwieriger und komplexer werden. Aber lassen wir das erst einmal beiseite.

[3]

Übersetzung in gewöhnliche Sprache: „am wenigsten mühsam“ („least tedious“).