Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft
Effektstärke
Die Berechnung der Effektstärke bei einer (mehr-)faktoriellen ANOVA ähnelt der bei der einfaktoriellen ANOVA (siehe Abschnitt Effektstärke). Insbesondere können wir η² (Eta-Quadrat) als einfaches Mittel verwenden, um zu messen, wie groß der Gesamteffekt für einen bestimmten Term ist. Wie zuvor beschrieben ist η² definiert, als die Quadratsumme, die mit diesem Term verbunden ist, geteilt durch die Gesamtquadratsumme. Um zum Beispiel die Effektstärke des Haupteffekts für Faktor A zu bestimmen, würden wir die folgende Formel verwenden:
Wie zuvor kann dieser Wert ähnlich interpretiert werden wie R² in der Regression.[1] Er gibt den Anteil der Varianz der Ergebnisvariablen an, der durch den Haupteffekt von Faktor A erklärt wird. Es handelt sich also um eine Zahl, die von 0 (überhaupt kein Effekt) bis 1 (erklärt die gesamte Variabilität in der Ergebnisvariablen) reicht. Darüber hinaus ergibt die Summe aller η²-Werte für alle Terme des Modells die Gesamtsumme R² für das ANOVA-Modell. Wenn das ANOVA-Modell beispielsweise perfekt passt (d. h. es gibt überhaupt keine Variabilität innerhalb der Gruppen auf den möglichen Faktorstufen), ergeben die η²-Werte den Wert 1. Natürlich kommt das in der Realität selten bis nie vor.
Beim Durchführen einer faktoriellen ANOVA gibt es jedoch ein zweites Maß für die Effektstärke, das gerne angegeben wird, nämlich das partielle η². Der Gedanke hinter dem partiellen η² (das manchmal auch als p η² oder η²p bezeichnet wird) ist, dass man bei der Messung der Effektstärke für einen bestimmten Term (z. B. den Haupteffekt von Faktor A) die anderen Effekte im Modell (z. B. den Haupteffekt von Faktor B) absichtlich ignorieren möchte. Das heißt, man würde so tun, als sei der Effekt all dieser anderen Terme gleich Null, und dann berechnen, wie hoch der η²-Wert gewesen wäre. Dies ist eigentlich recht einfach zu berechnen. Sie müssen lediglich die Quadratsumme der anderen Terme aus dem Nenner entfernen. Mit anderen Worten, wenn Sie den partiellen η²-Wert für den Haupteffekt von Faktor A suchen, ist der Nenner einfach die Summe der SS-Werte für Faktor A und die Residuen
Dadurch erhält man immer eine größere Zahl als η², was, wie der Zyniker in mir vermutet, der Grund für die Beliebtheit vom partiellen η² ist. Und auch hier erhält man eine Zahl zwischen 0 und 1, wobei 0 für keinen Effekt steht. Allerdings ist es etwas schwieriger zu interpretieren, was ein großer partieller η²-Wert bedeutet. Vor allem kann man die partiellen η²-Werte nicht zwischen den Termen vergleichen! Angenommen, es gibt überhaupt keine Variabilität innerhalb von Gruppen: dann ist SSR = 0. Das bedeutet, dass jeder -Term einen partiellen η²-Wert von 1 hat. Das bedeutet aber nicht, dass alle Terme in Ihrem Modell gleich wichtig sind oder dass sie gleich groß sind. Es bedeutet lediglich, dass alle Terme in Ihrem Modell Effektstärken haben, die relativ zur Restvariation groß sind. Es ist nicht zwischen den Termen vergleichbar.
Um zu sehen, was ich damit meine, ist es nützlich, ein konkretes Beispiel zu betrachten. Schauen wir uns zunächst die Effektstärken für die ursprüngliche ANOVA ohne den Interaktionsterm aus Abb. 146 an:
eta.sq partial.eta.sq
drug 0.71 0.79
therapy 0.10 0.34
Betrachtet man zunächst die η²-Werte, so stellt man fest, dass drug 71 % der Varianz (d. h. η² = 0,71) in mood.gain erklärt, therapy jedoch nur 10 %. Damit verbleiben insgesamt 19 % der Varianz unaufgeklärt (d. h. die Residuen machen 19 % der Varianz des Ergebnisses aus). Insgesamt bedeutet dies, dass wir einen sehr großen Effekt[2] von drug und einen deutlich kleineren Effekt von therapy haben.
Schauen wir uns nun die partiellen η²-Werte an, die in Abb. 146 gezeigt werden. Da der Effekt von therapy nicht sehr groß ist, macht die Kontrolle dafür keinen großen Unterschied, so dass der partielle η²-Wert für drug nicht sehr stark ansteigt, und wir erhalten einen Wert von pη² = 0,79). Da der Effekt von drug dagegen sehr groß war, macht die Kontrolle dafür einen großen Unterschied, und wenn wir das partielle η² für therapy berechnen, können wir sehen, dass er auf pη² = 0,34 ansteigt. Die Frage, die wir uns stellen müssen, ist, was bedeuten diese partiellen η²-Werte eigentlich? Die Art und Weise, wie ich im Allgemeinen den partiellen η²-Wert für den Haupteffekt von Faktor A interpretiere, besteht darin, ihn als eine Aussage über ein hypothetisches Experiment zu interpretieren, in dem nur Faktor A variiert wurde. Obwohl wir also in diesem Experiment sowohl A als auch B variiert haben, können wir uns leicht ein Experiment vorstellen, in dem nur Faktor A variiert wurde. Die partielle η²-Statistik gibt dann an, wie viel der Varianz in der Ergebnisvariablen in diesem Experiment voraussichtlich aufgeklärt werden würde. Es ist jedoch anzumerken, dass diese Interpretation, wie viele Dinge im Zusammenhang mit Haupteffekten, nicht viel Sinn macht, wenn es einen großen und signifikanten Interaktionseffekt gibt.
Apropos Interaktionseffekte: Hier sehen Sie, was wir erhalten, wenn wir die Effektstärken für das Modell berechnen, das den Interaktionsterm enthält, wie in Abb. 150. Wie Sie sehen können, ändern sich die η²-Werte für die Haupteffekte nicht, wohl aber die partiellen η²-Werte:
eta.sq partial.eta.sq
drug 0.71 0.84
therapy 0.10 0.42
drug*therapy 0.06 0.29
Geschätzte Gruppenmittelwerte
In vielen Situationen werden Sie Schätzungen für alle Gruppenmittelwerte auf der Grundlage der Ergebnisse Ihrer ANOVA sowie die zugehörigen Konfidenzintervalle ausgeben wollen. Sie können dazu die Option Estimated Marginal Means in der jamovi ANOVA-Analyse verwenden (wie in Abb. 151 gezeigt). Wenn die von Ihnen durchgeführte ANOVA ein gesättigtes Modell ist (d.h. alle möglichen Haupteffekte und alle möglichen Interaktionseffekte enthält), dann sind die Schätzungen der Gruppenmittelwerte tatsächlich identisch mit den Stichprobenmittelwerten, obwohl die Konfidenzintervalle eine gepoolte Schätzung der Standardfehler verwenden, anstatt eine separate für jede Gruppe zu verwenden.
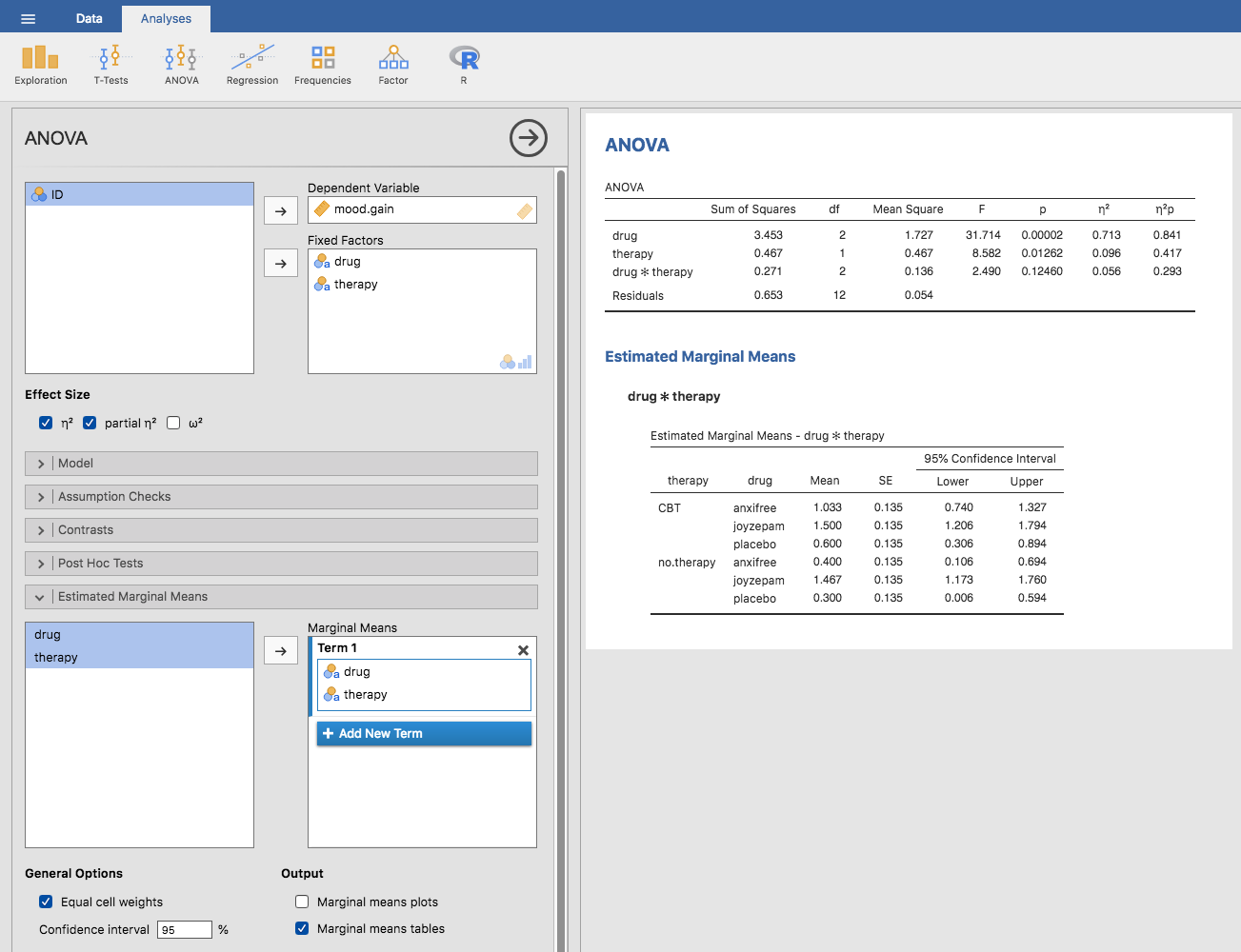
Abb. 151 jamovi-Screenshot mit den geschätzten Randmitteln für das gesättigte Modell, d. h. einschließlich der Interaktionskomponente, mit dem Datensatz clinicaltrial
In der Ausgabe sehen wir, dass der geschätzte mittlere Stimmungszuwachs für die Placebogruppe ohne Therapie 0,300 beträgt, mit einem 95%-Konfidenzintervall von 0,006 bis 0,594. Beachten Sie, dass dies nicht die gleichen Konfidenzintervalle sind, die Sie erhalten würden, wenn Sie sie für jede Gruppe separat berechnen würden, da das ANOVA-Modell von homogenen Varianzen ausgeht und daher eine gepoolte Schätzung der Standardabweichung verwendet.
Wenn das Modell den Interaktionsterm nicht enthält, unterscheiden sich die geschätzten Gruppenmittelwerte von den Stichprobenmittelwerten. Anstatt den Stichprobenmittelwert anzugeben, berechnet jamovi den Wert der Gruppenmittelwerte, der auf der Grundlage der Randmittel zu erwarten wäre (d. h. unter der Annahme, dass keine Interaktion vorliegt). Unter Verwendung der zuvor entwickelten Notation würde die Schätzung für µrc, den Mittelwert für die Ebene r auf dem (Zeilen-) Faktor A und die Ebene c auf dem (Spalten-) Faktor B, µ.. + αr + βclauten. Wenn es wirklich keine Wechselwirkungen zwischen den beiden Faktoren gibt, ist dies tatsächlich eine bessere Schätzung des Populationsmittelwerts als es der rohe Stichprobenmittelwert wäre. Das Entfernen des Interaktionsterms aus dem Modell über die Optionen Model in der jamovi ANOVA-Analyse liefert die Randmittel für die in Abb. 152 dargestellte Analyse.
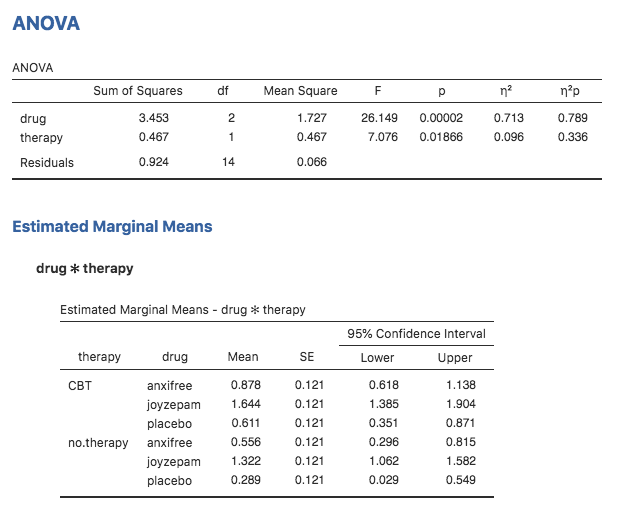
Abb. 152 jamovi-Screenshot zeigt die geschätzten Randmittel für das ungesättigte Modell, d.h. ohne die Interaktionskomponente, mit dem Datensatz clinicaltrial