Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft
Die ANOVA als lineares Modell
Eines der wichtigsten Dinge, die man über ANOVA und Regression wissen muss, ist, dass sie im Grunde dasselbe sind. Oberflächlich betrachtet, würden Sie das vielleicht nicht denken. Außerdem lässt die Art und Weise, wie ich sie bisher beschrieben habe, vermuten, dass es bei der ANOVA in erster Linie um das Testen von Gruppenunterschieden und bei der Regression in erster Linie um das Verständnis der Korrelationen zwischen Variablen geht. Das ist auch vollkommen korrekt. Aber wenn man unter die Haube schaut, sind sich die zugrundeliegenden Mechanismen von ANOVA und Regression ziemlich ähnlich. Wenn Sie darüber nachdenken, haben Sie bereits Belege dafür gesehen. Sowohl die ANOVA als auch die Regression stützen sich in hohem Maße auf Quadratsummen (SS), beide verwenden F-Tests und so weiter. Im Rückblick kann man sich des Eindrucks nicht erwehren, dass die Kapitel Korrelation und lineare Regression und Vergleich mehrerer Mittelwerte (einfaktorielle ANOVA) ein wenig repetitiv waren.
Der Grund dafür ist, dass sowohl ANOVA als auch Regression auf linearen Modellen basieren. Im Falle der Regression ist dies ziemlich offensichtlich. Die Regressionsgleichung, die wir verwenden, um die Beziehung zwischen den Prädiktoren und den Ergebnissen zu definieren ist die Gleichung für eine gerade Linie, es handelt sich also ganz offensichtlich um ein lineares Modell mit der Gleichung
wobei Yp der Ergebniswert für die p-te Beobachtung ist (z. B., p-te Person), X1p der Wert des ersten Prädiktors für die p-te Beobachtung ist, X2p der Wert des zweiten Prädiktors für die p-te Beobachtung ist, die b0, b1 und b2 sind unsere Regressionskoeffizienten, und ϵp ist das Residuum für die p-te Person. Wenn wir die Residuen ϵp ignorieren und uns nur auf die Regressionsgerade selbst konzentrieren, erhalten wir die folgende Formel:
wobei Ŷp der Wert von Y ist, den die Regressionsgerade für die Person p vorhersagt, im Gegensatz zu dem tatsächlich beobachteten Wert Yp. Was nicht sofort ersichtlich ist, ist, dass wir die ANOVA auch als lineares Modell schreiben können. Es ist jedoch ziemlich einfach, dies zu tun. Beginnen wir mit einem ganz einfachen Beispiel, indem wir eine 2 × 2 faktorielle ANOVA in ein lineares Modell umschreiben.
Ein Beispiel mit Daten
Um die Dinge zu konkretisieren, nehmen wir an, dass unsere Ergebnisvariable der grade ist, den ein Student in meiner Klasse erhält; eine Variable auf Verhältnisskalenniveau, die einer Note von 0 bis 100 % entspricht. Es gibt zwei Prädiktorvariablen, die von Interesse sind: ob der Student die Vorlesungen besucht hat oder nicht (die Variable attend) und ob der Student das Lehrbuch gelesen hat oder nicht (die Variable reading). Wir sagen, dass attend = 1 bedeutet, dass der Student die Vorlesung besucht hat, und attend = 0, dass er sie nicht besucht hat. Gleichermaßen sagen wir, dass reading = 1 bedeutet, dass der Student das Lehrbuch gelesen hat, und reading = 0, dass er es nicht getan hat.
So weit ist das einfach genug. Das nächste, was wir tun müssen, ist, dies mit ein wenig Mathematik anzureichern (sorry!). Für die Zwecke dieses Beispiels sei Yp die grade des p-ten Schülers in der Klasse bezeichnet. Dies ist nicht ganz die gleiche Notation, die wir früher in diesem Kapitel verwendet haben. Zuvor haben wir die Notation Yrci verwendet, um die i-te Person in der r-ten Gruppe für Prädiktor 1 (den Zeilenfaktor) und die c-te Gruppe für Prädiktor 2 (den Spaltenfaktor) zu bezeichnen. Diese erweiterte Notation war wirklich praktisch, um zu beschreiben, wie die SS-Werte berechnet werden, aber im aktuellen Kontext ist sie lästig, also werde ich die Notation hier ändern. Die Notation Yp ist visuell einfacher als Yrci, hat aber den Nachteil, dass sie die Gruppenzugehörigkeit nicht zeigt. Das heißt, wenn ich Ihnen sagen würde, dass Y0,0,3 = 35 ist, wüssten Sie sofort, um welchen Studenten es sich handelt (den dritten Studenten), der die Vorlesungen nicht besucht hat (d.h. attend = 0) und das Lehrbuch nicht gelesen hat (d.h. reading = 0) und schließlich durch den Kurs gefallen ist (grade = 35). Aber wenn ich Ihnen sage, dass Yp = 35 ist, wissen Sie nur, dass der p-te Schüler keine gute Note bekommen hat. Wir haben hier einige wichtige Informationen verloren. Natürlich muss man nicht lange nachdenken, um herauszufinden, wie man das beheben kann. Stattdessen werden wir zwei neue Variablen X1p und X2p einführen, die diese Informationen aufbewahren. Im Fall unseres hypothetischen Schülers wissen wir, dass X1p = 0 (d.h., attend = 0) und X2p = 0 (d.h., reading = 0). Die Daten könnten also wie folgt aussehen:
Person, p |
Note, Yp |
Anwesenheit, X1p |
Lehrbuch gelesen, X2p |
|---|---|---|---|
1 |
90 |
1 |
1 |
2 |
87 |
1 |
1 |
3 |
75 |
0 |
1 |
4 |
60 |
1 |
0 |
5 |
35 |
0 |
0 |
6 |
50 |
0 |
0 |
7 |
65 |
1 |
0 |
8 |
70 |
0 |
1 |
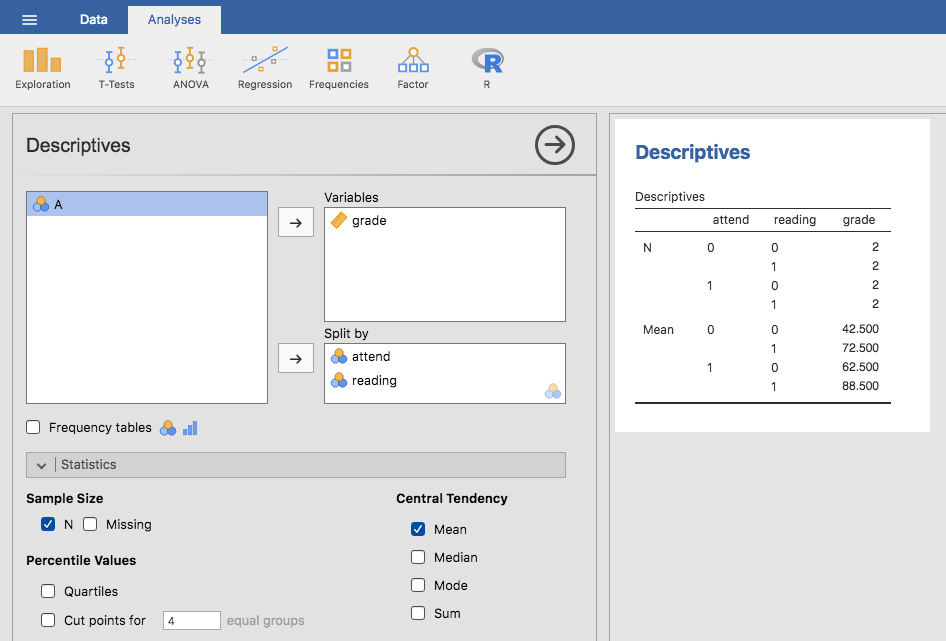
Das ist natürlich nichts Besonderes, sondern genau das Format, in dem wir unsere Daten erwarten. Wenn wir den Datensatz rtfm verwenden, können wir die jamovi-Analyse Descriptives verwenden, um zu bestätigen, dass dieser Datensatz einem ausgewogenen Design entspricht, mit 2 Beobachtungen für jede Kombination von attend und reading. Auf die gleiche Weise können wir auch den Mittelwert der Note für jede Kombination berechnen. Dies wird in Abb. 159 gezeigt. Wenn man sich die Durchschnittsnoten ansieht, bekommt man den Eindruck, dass sowohl das Lesen des Textes als auch die Teilnahme am Unterricht eine große Rolle für die Note spielen.
ANOVA mit binären Faktoren als Regressionsmodell
Lassen Sie uns wieder über die Mathematik sprechen. Wir haben jetzt unsere Daten in Form von drei numerischen Variablen ausgedrückt: die kontinuierliche Variable Y und die beiden binären Variablen X1 und X2. Ich möchte, dass Sie erkennen, dass unsere 2 × 2 faktorielle ANOVA genau dem Regressionsmodell entspricht:
Dies ist natürlich genau die gleiche Gleichung, die ich zuvor zur Beschreibung eines Regressionsmodells mit zwei Prädiktoren verwendet habe! Der einzige Unterschied besteht darin, dass X1 und X2 nun binäre Variablen sind (d.h. die Werte können nur 0 oder 1 sein), während wir bei einer Regressionsanalyse erwarten, dass X1 und X2 kontinuierlich sind. Es gibt mehrere Möglichkeiten, wie ich versuchen könnte, Sie davon zu überzeugen. Eine Möglichkeit wäre, eine langwierige mathematische Analyse durchzuführen, um zu beweisen, dass die beiden identisch sind. Ich lehne mich stattdessen weit aus dem Fenster und vermute, dass die meisten Leser dieses Buches das eher lästig als hilfreich finden würden. Stattdessen werde ich die grundlegenden Ideen erklären und mich dann auf jamovi verlassen, um zu zeigen, dass ANOVA-Analysen und Regressionsanalysen nicht nur ähnlich, sondern in jeder Hinsicht identisch sind. Beginnen wir damit, dies als ANOVA durchzuführen. Dazu verwenden wir den Datensatz rtfm, und Abb. 160 zeigt, was wir erhalten, wenn wir die Analyse in jamovi ausführen.
Abb. 160 ANOVA des Datensatzes rtfm in jamovi: Modell mit zwei Faktoren attend und reading, aber ohne den Interaktionsterm für diese beiden Faktoren
Wenn wir also die Ergebnisse aus der ANOVA-Tabelle mit den Mittelwerte aus unserer früheren Analyse vergleichen, so können wir sehen, dass die Schüler eine bessere Note erhielten, wenn sie am Unterricht teilnahmen (F(1,5) = 21,6, p = 0,0056) und wenn sie das Lehrbuch gelesen haben: F(1,5) = 52,3,*p* = 0,0008. Notieren wir uns diese p-Werte und diese F-Statistiken.
Betrachten wir nun die gleiche Analyse aus der Perspektive der linearen Regression. Im Datensatz rtfm haben wir attend und reading so kodiert, als wären sie numerische Prädiktoren. In diesem Fall ist dies durchaus akzeptabel. Ein Schüler, der zum Unterricht erscheint (d.h. attend = 1), hat in der Tat „mehr Anwesenheit“ geleistet als ein Schüler, der nicht erscheint (d.h. attend = 0). Es ist also gar nicht so unvernünftig, dies als Prädiktor in ein Regressionsmodell aufzunehmen. Es ist ein wenig ungewöhnlich, weil der Prädiktor nur einen von zwei möglichen Werten annehmen kann, aber es verletzt keine der Annahmen der linearen Regression. Und es ist leicht zu interpretieren. Wenn der Regressionskoeffizient für attend größer ist als 0 ist, bedeutet das, dass Studenten, die Vorlesungen besuchen, bessere Noten bekommen. Ist der Koeffizient kleiner als Null, dann haben die Studenten, die an Vorlesungen teilnehmen, schlechtere Noten. Das Gleiche gilt für unsere Variable reading.
Aber warten Sie eine Sekunde. Warum ist das wahr? Es ist etwas, das intuitiv für jeden offensichtlich ist, der ein paar Statistikkurse besucht hat und mit der Mathematik vertraut ist, aber allen anderen ist es nicht auf Anhieb klar. Um zu sehen, warum das so ist, hilft es, sich ein paar ausgewählte Schüler genauer anzusehen. Betrachten wir zunächst den 6. und den 7. Schüler in unserem Datensatz (d. h. p = 6 und p = 7). Keiner von ihnen hat das Lehrbuch gelesen, also können wir in beiden Fällen reading = 0 einstellen. Oder, um dasselbe in unserer mathematischen Notation zu sagen, wir beobachten X2,6 = 0 und X2,7 = 0. Student Nummer 7 ist jedoch zu den Vorlesungen erschienen (d.h., attend = 1, X1,7 = 1), während Student Nummer 6 nicht erschien (d.h. attend = 0, X1,6 = 0). Sehen wir uns nun an, was passiert, wenn wir diese Zahlen in die allgemeine Formel für unsere Regressionsgerade einsetzen. Für Schüler Nummer 6 sagt die Regression voraus, dass:
Wir gehen also davon aus, dass dieser Schüler eine Note erhält, die dem Wert des Interzept Terms b0 entspricht. Was ist mit dem 7. Schüler? Wenn wir dieses Mal die Zahlen in die Formel für die Regressionsgerade einsetzen, erhalten wir folgendes Ergebnis:
Da dieser Student an den Vorlesungen teilgenommen hat, ist die vorhergesagte Note gleich dem Interzept-Term b0 plus dem Koeffizienten, der mit der Variable attend verbunden ist, b1. Wenn also b1 größer als Null ist, erwarten wir, dass die Studenten, die zu den Vorlesungen erscheinen, bessere Noten bekommen als die Studenten, die nicht kommen. Wenn dieser Koeffizient negativ ist, erwarten wir das Gegenteil: Studierende, die zu den Vorlesungen erscheinen, erbringen schlechtere Leistungen. Wir können das Ganze sogar noch ein bisschen weiter treiben. Was ist mit dem 1. Schüler, der zum Unterricht erschienen ist (X1,1 = 1) und das Lehrbuch gelesen hat (X2,1 = 1)? Wenn wir diese Zahlen in die Regression einsetzen, erhalten wir:
Wenn wir also davon ausgehen, dass die Teilnahme am Unterricht zu einer guten Note beiträgt (d.h., b1 > 0) und wenn wir annehmen, dass das Lesen des Lehrbuchs ebenfalls zu einer guten Note beiträgt (d.h., b2 > 0), dann ist unsere Erwartung, dass der 1. Schüler eine bessere Note erhält als der 6. und der 7. Schüler.
Und an dieser Stelle wird es Sie nicht überraschen, dass das Regressionsmodell vorhersagt, dass der 3. Schüler, der das Buch gelesen, aber nicht an den Vorlesungen teilgenommen hat, eine Note von b2 + b0 erhalten wird. Ich werde Sie nicht mit einer weiteren Regressionsformel langweilen. Stattdessen zeige ich Ihnen die folgende Tabelle der erwarteten Noten:
Lehrbuch gelesen? |
|||
|---|---|---|---|
Nein |
Ja |
||
An Vorlesungen teilgenommen? |
Nein |
b0 |
b0 + b2 |
Ja |
b0 + b1 |
b0 + b1 + b2 |
|
Wie Sie sehen, fungiert der Intercept-Term b0 als eine Art „Basisnote“, die Sie von denjenigen Schülern erwarten würden, die sich nicht die Zeit nehmen, den Unterricht zu besuchen oder das Lehrbuch zu lesen. In ähnlicher Weise steht b1 für die Verbesserung, die man erwartet, wenn der Schüler zum Unterricht kommt, und b2 für die Verbesserung, die man durch das Lesen des Lehrbuchs erhält. Wäre dies eine ANOVA, könnte man b1 als den Haupteffekt der Anwesenheit und b2 als den Haupteffekt des Lesens bezeichnen! Bei einer einfachen 2 × 2 ANOVA entspricht das genau der Realität.
Da wir jetzt langsam beginnen, zu verstehen, warum ANOVA und Regression im Grunde dasselbe sind, führen wir unsere Regression mit dem rtfm-Datensatz und der jamovi-Regressionsanalyse durch, um uns davon zu überzeugen, dass dies wirklich so ist. Das Durchführen der Regression auf die übliche Weise ergibt die in Abb. 161 dargestellten Ergebnisse.
Abb. 161 Regressionsanalyse für den rtfm-Datensatz in jamovi: Modell mit zwei Faktoren attend und reading, aber ohne den Interaktionsterm dieser beiden Faktoren
Hier gibt es einige interessante Dinge zu beachten. Zunächst fällt auf, dass der Interzept-Term 43,5 beträgt, was nahe am „Gruppen“-Mittelwert von 42,5 liegt, der für die beiden Schüler beobachtet wurde, die weder den Text gelesen noch den Unterricht besucht haben. Zweitens ist der Regressionskoeffizient b1 = 18,0 für die Anwesenheitsvariable, was darauf hindeutet, dass die Schüler, die am Unterricht teilgenommen haben, eine um 18 % höhere Punktzahl erzielt haben als die, welche nicht teilgenommen haben. Unsere Erwartung wäre also, dass die Schüler, die zum Unterricht erschienen sind, aber das Lehrbuch nicht gelesen haben, eine Note von b0 + b1 erhalten würden, was 43,5 + 18,0 = 61,5 entspricht. Sie können selbst überprüfen, dass dasselbe passiert, wenn wir uns die Schüler ansehen, die das Lehrbuch gelesen haben.
Wir können sogar noch etwas weiter gehen, um die Gleichwertigkeit unserer ANOVA und unserer Regression festzustellen. Sehen Sie sich die p-Werte an, die mit der Variable attend und der Variable reading in der Ergebnisausgabe der Regression verbunden sind. Sie sind identisch mit denen, die wir zuvor beim Durchführen der ANOVA erhalten haben. Dies mag ein wenig überraschen, da der Test, der in unserem Regressionsmodell verwendet wird, eine t-Statistik berechnet und die ANOVA eine F-Statistik berechnet. Wenn Sie sich jedoch an das Kapitel Einführung in die Wahrscheinlichkeitsrechnung zurückerinnern, habe ich dort erwähnt, dass es eine Beziehung zwischen der t-Verteilung und der F-Verteilung gibt. Wenn man eine Menge hat, die gemäß einer t-Verteilung mit k Freiheitsgraden verteilt ist, und man quadriert sie, dann folgt diese neue quadrierte Menge einer F-Verteilung, deren Freiheitsgrade 1 und k sind. Wir können dies in Bezug auf die t-Statistik in unserem Regressionsmodell überprüfen. Für die Variable attend erhalten wir einen t-Wert von 4,65. Wenn wir diese Zahl quadrieren, erhalten wir 21,6, was mit der entsprechenden F-Statistik in unserer ANOVA übereinstimmt.
Zum Schluss noch eine letzte Sache, die Sie wissen sollten. Da jamovi weiß, dass sowohl ANOVA als auch Regression Beispiele für lineare Modelle sind, können Sie die klassische ANOVA-Tabelle aus Ihrem Regressionsmodell extrahieren, indem Sie Linear Regression - Model Coefficients - Omnibus Test - ANOVA test wählen. Sie erhalten dann die in Abb. 162 gezeigte Tabelle.
Abb. 162 Ergebnistabelle mit dem ANOVA-Test für das gesamte Modell innerhalb der Regressionsanalyse mit dem Datensatz rtfm in jamovi
Wie man nicht-binäre Faktoren als Kontraste kodiert
An dieser Stelle habe ich Ihnen gezeigt, wie wir eine 2 × 2 ANOVA als lineares Modell betrachten können. Und es ist ziemlich einfach zu sehen, wie sich dies auf eine 2 × 2 × 2 ANOVA oder eine 2 × 2 × 2 × 2 ANOVA verallgemeinern lässt. Es ist im Grunde dasselbe. Sie fügen einfach eine neue binäre Variable für jeden Ihrer Faktoren hinzu. Schwieriger wird es, wenn wir Faktoren mit mehr als zwei Stufen betrachten. Nehmen wir zum Beispiel die 3 × 2 ANOVA, die wir früher in diesem Kapitel mit dem Datensatz clinicaltrial durchgeführt haben. Wie können wir den dreistufigen drug-Faktor in eine numerische Form umwandeln, die für eine Regression geeignet ist?
Die Antwort auf diese Frage ist eigentlich ziemlich einfach. Man muss sich nur klarmachen, dass ein dreistufiger Faktor als zwei binäre Variablen neu beschrieben werden kann. Nehmen wir zum Beispiel an, ich würde eine neue binäre Variable mit dem Namen druganxifree erstellen. Immer wenn die Variable drug gleich anxifree ist, setzen wir druganxifree = 1. Andernfalls setzen wir druganxifree = 0. Diese Variable bildet einen Gegensatz, in diesem Fall zwischen anxifree und den beiden anderen Drogen. Der Kontrast druganxifree allein reicht natürlich nicht aus, um alle Informationen in unserer Variable drug vollständig zu erfassen. Wir brauchen einen zweiten Kontrast, der es uns ermöglicht, zwischen joyzepam und placebo zu unterscheiden. Zu diesem Zweck können wir einen zweiten binären Kontrast mit der Bezeichnung drugjoyzepam erstellen, der gleich 1 ist, wenn drug joyzepam ist, und 0, wenn dies nicht der Fall ist. Zusammengenommen ermöglichen uns diese beiden Kontraste eine perfekte Unterscheidung zwischen allen drei möglichen Stufen von drug. Die folgende Tabelle veranschaulicht dies:
|
|
|
|
0 |
0 |
|
1 |
0 |
|
0 |
1 |
Wenn die drug, die einem Patienten verabreicht wurde, ein placebo ist, dann sind beide Kontrastvariablen gleich 0. Wenn die drug anxifree ist, dann ist die druganxifree Variable gleich 1, und drugjoyzepam ist 0. Umgekehrt gilt für joyzepam: drugjoyzepam ist dann 1 und druganxifree ist 0.
Das Erstellen von Kontrastvariablen ist nicht allzu schwierig: Wenn Sie in jamovi New Computed Variable verwenden, um eine neue berechnete Variable zu erstellen. Um zum Beispiel die Variable druganxifree zu erstellen, schreiben Sie den folgenden logischen Ausdruck in das Formelfeld: IF(drug == 'anxifree', 1, 0). Um die Variable drugjoyzepam zu erstellen, verwenden Sie den folgenden logischen Ausdruck: IF(drug == 'joyzepam', 1, 0). Das Gleiche gilt für CBTtherapy: IF(therapy == 'CBT', 1, 0). Sie können diese neuen Variablen und die entsprechenden logischen Ausdrücke im Datensatz clinicaltrial2 sehen.
Wir haben nun unseren dreistufigen Faktor in zwei binäre Variablen umkodiert, und wir haben bereits gesehen, dass sich ANOVA und Regression bei binären Variablen gleich verhalten. Allerdings ergeben sich in diesem Fall einige zusätzliche Komplexitäten, die wir im nächsten Abschnitt erörtern werden.
Die Gleichwertigkeit von ANOVA und Regression für nicht-binäre Faktoren
Wir haben nun zwei verschiedene Versionen desselben Datensatzes. Unsere ursprünglichen Daten, in denen die Variable drug aus dem clinicaltrial-Datensatz als ein einziger dreistufiger Faktor ausgedrückt wird, und der clinicaltrial2-Datensatz, in dem sie in zwei binäre Kontraste zerlegt wird. Auch hier wollen wir zeigen, dass unsere ursprüngliche 3 × 2 faktorielle ANOVA einem auf die Kontrastvariablen angewandten Regressionsmodell entspricht. Beginnen wir mit dem erneuten Durchführen der ANOVA, deren Ergebnisse in Abb. 163 gezeigt werden.
Abb. 163 jamovi ANOVA-Ergebnisse für den clinicaltrial-Datensatz: Ungesättigtes Modell mit den beiden Haupteffekten für drug und therapy, aber ohne eine Interaktionskomponente für diese beiden Faktoren
Offenbar gibt es auch hier keine Überraschungen. Es handelt sich um genau dieselbe ANOVA, die wir zuvor durchgeführt haben. Als Nächstes führen wir eine Regression mit druganxifree, drugjoyzepam und CBTtherapy als Prädiktoren durch. Die Ergebnisse sind in Abb. 164 dargestellt.
Abb. 164 jamovi-Ergebnisse für das Regressionsmodell mit den generierten Kontrastvariablen druganxifree und drugjoyzepam aus dem clinicaltrial Datensatz
Dies ist nicht die gleiche Ausgabe wie beim letzten Mal. Es überrascht nicht, dass die Regressionsausgabe die Ergebnisse für jeden der drei Prädiktoren separat ausgibt, genau wie bei jeder anderen Regressionsanalyse, die wir durchgeführt haben. Einerseits können wir sehen, dass der p-Wert für die Variable CBTtherapy genau derselbe ist wie der für den Faktor therapy in unserer ursprünglichen ANOVA, so dass wir beruhigt sein können, dass das Regressionsmodell das Gleiche tut wie die ANOVA. Andererseits testet dieses Regressionsmodell den
druganxifree-Kontrast und den drugjoyzepam-Kontrast separat, als ob es sich um zwei völlig unverbundene Variablen handeln würde. Das ist natürlich nicht überraschend, denn die Regressionsanalyse hat keine Möglichkeit zu „wissen“, dass drugjoyzepam und druganxifree die beiden verschiedenen Kontraste sind, die wir zur Kodierung unseres dreistufigen drug Faktors verwendet haben. Für die Regressionsanalyse, sind drugjoyzepam und druganxifree genauso wenig miteinander verbunden wie drugjoyzepam und therapyCBT. Sie und ich wissen es dagegen besser. In diesem Stadium sind wir überhaupt nicht daran interessiert, festzustellen, ob diese beiden Kontraste einzeln signifikant sind. Wir wollen nur wissen, ob es einen „Gesamteffekt“ von drug gibt. Das heißt, wir wollen, dass jamovi eine Art „Modellvergleichstest“ durchführt, bei dem die beiden „medikamentbezogenen“ Kontraste für die Zwecke des Tests zusammen analysiert werden. Kommt Ihnen das bekannt vor? Alles, was wir tun müssen, ist, unser Nullmodell zu spezifizieren, das in diesem Fall den CBTtherapy-Prädiktor einschließt und beiden medikamentbezogenen Variablen weglassen würde, wie in Abb. 165.
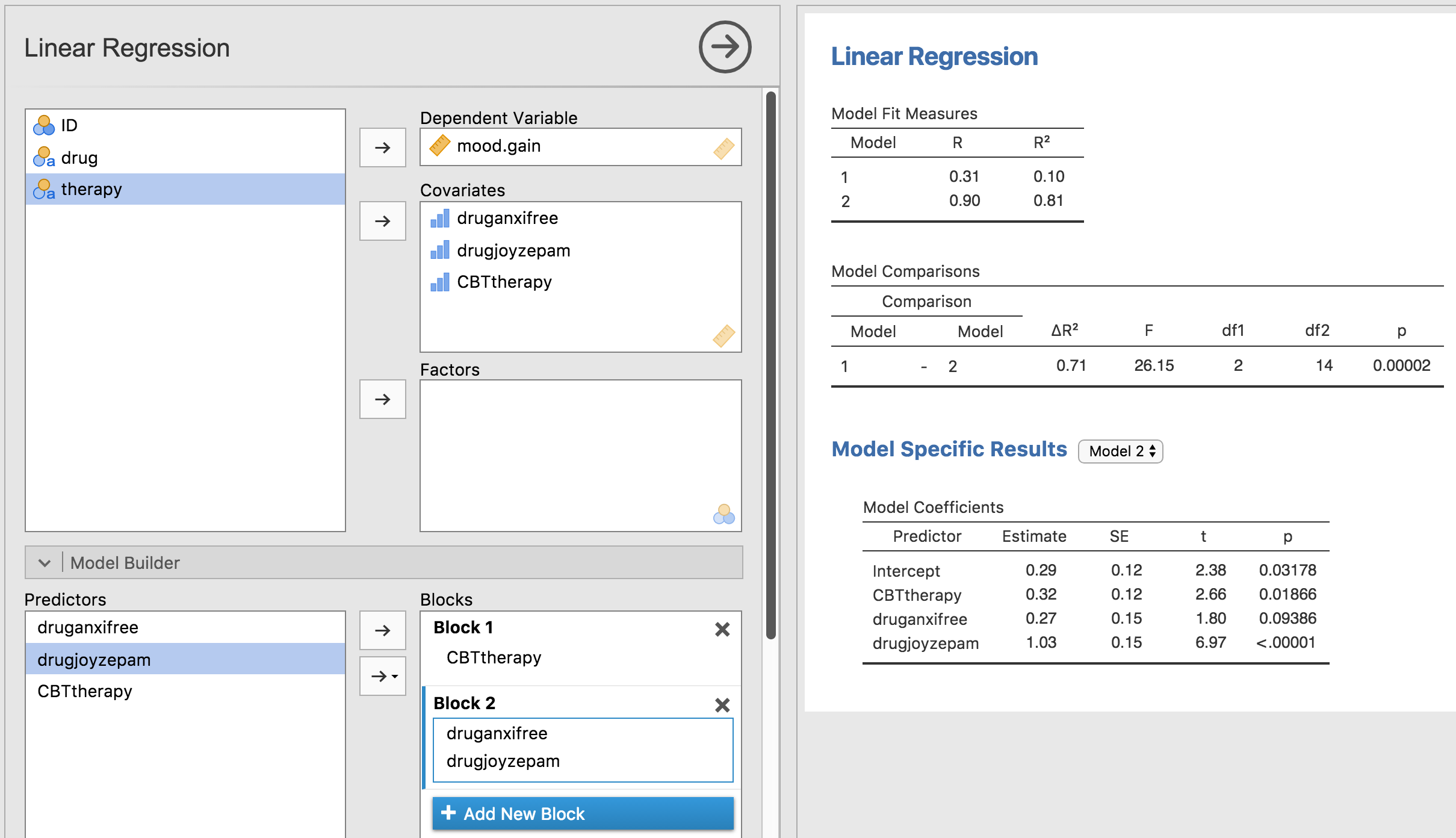
Abb. 165 Modellvergleich in der jamovi-Regressionsanalyse: Nullmodell (Modell 1) vs. Modell mit den generierten Kontrastvariablen (Modell 2)
Ah, so ist es besser. Unsere F-Statistik ist 26,15, die Freiheitsgrade sind 2 und 14, und der p-Wert ist 0,00002. Die Zahlen sind identisch mit denen, die wir für den Haupteffekt von drug in unserer ursprünglichen ANOVA erhalten haben. Wieder einmal sehen wir, dass ANOVA und Regression im Wesentlichen das Gleiche sind. Es sind beides lineare Modelle, und die zugrundeliegende statistische Maschinerie für die ANOVA ist identisch mit der Maschinerie, die in der Regression verwendet wird. Die Bedeutung dieser Tatsache sollte nicht unterschätzt werden. Im weiteren Verlauf dieses Kapitels werden wir uns auf diesen Gedanken aufbauen.
Obwohl wir uns die Mühe gemacht haben, in jamovi neue Variablen für die Kontraste druganxifree und drugjoyzepam zu berechnen, nur um zu zeigen, dass ANOVA und Regression im Wesentlichen das Gleiche sind, gibt es in der Regressionsanalyse von jamovi eine raffinierte Abkürzung, um diese Kontraste zu erhalten, siehe Abb. 166. Was jamovi hier macht, ist, dass es Ihnen erlaubt, die Prädiktorvariablen, die Faktoren sind, als - warten Sie es ab - Faktoren einzugeben! Clever, oder? Mit der Option Reference Levels können Sie angeben, welche Gruppe als Referenzebene (Ausgangs- bzw. Vergleichsniveau) verwendet werden soll. Wir haben dies in placebo bzw. no.therapy geändert, da dies am sinnvollsten ist.
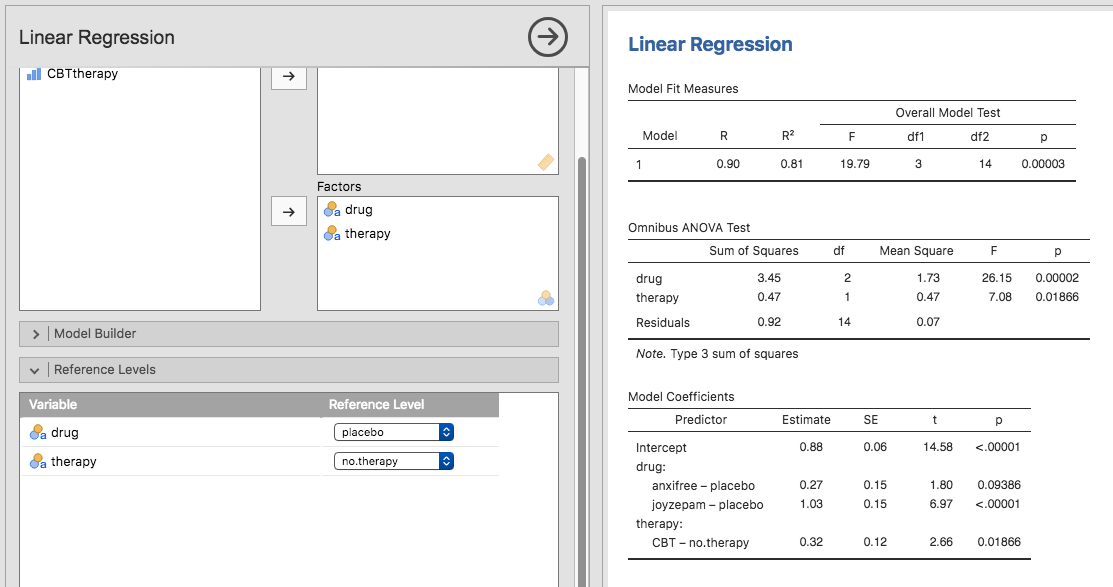
Abb. 166 Regressionsanalyse mit Faktoren und Kontrasten in jamovi, einschließlich der Ergebnisse des ANOVA-Tests für das gesamte Modell
Wenn Sie die Checkbox ANOVA test unter der Option Model Coefficients → Omnibus Test aktivieren, sehen wir, dass die F-Statistik 26,15 beträgt, die Freiheitsgrade 2 und 14 sind und der p-Wert 0,00002 ist (siehe Abb. 166). Die Zahlen sind identisch mit denen, die wir für den Haupteffekt von drug in unserer ursprünglichen ANOVA erhalten haben. Wieder einmal zeigt sich, dass ANOVA und Regression im Wesentlichen dasselbe sind. Es sind beides lineare Modelle, und die zugrundeliegende statistische Maschinerie für ANOVA ist identisch mit der Maschinerie, die in der Regression verwendet wird.
Freiheitsgrade als Parameterzahl
Endlich kann ich eine Definition von Freiheitsgraden geben, mit der ich zufrieden bin. Freiheitsgrade werden in Bezug auf die Anzahl der Parameter definiert, die in einem Modell geschätzt werden müssen. Bei einem Regressionsmodell oder einer ANOVA entspricht die Anzahl der Parameter der Anzahl der Regressionskoeffizienten (d. h. b-Werte), einschließlich des Interzepts. Dabei ist zu beachten, dass jeder F-Test immer ein Vergleich zwischen zwei Modellen ist und der erste df die Differenz in der Anzahl der Parameter ist. Im obigen Modellvergleich hat das Nullmodell (mood.gain ~ therapyCBT) zum Beispiel zwei Parameter: Es gibt einen Regressionskoeffizienten für die Variable therapyCBT und einen zweiten für das Interzept. Das Alternativmodell (mood.gain ~ druganxifree + drugjoyzepam + therapyCBT) hat vier Parameter: einen Regressionskoeffizienten für jeden der drei Kontraste und einen weiteren für das Interzept. Die Freiheitsgrade für den Unterschied zwischen diesen beiden Modellen sind also df1 = 4 - 2 = 2.
Was ist mit dem Fall, dass es kein Nullmodell zu geben scheint? Sie denken vielleicht an den F-Test, der angezeigt wird, wenn Sie F Test unter den Optionen Linear Regression - Model Fit auswählen. Ursprünglich habe ich diesen Test als einen Test des Regressionsmodells als Ganzes beschrieben. Es ist jedoch immer ein Vergleich zwischen zwei Modellen. Das Nullmodell ist das triviale Modell, das nur einen Regressionskoeffizienten für den Interzept-Term enthält. Das Alternativmodell enthält K + 1 Regressionskoeffizienten, einen für jede der K Prädiktorvariablen und einen weiteren für das Interzept. Der df-Wert, den Sie in diesem F-Test sehen, ist also gleich df1 = K + 1 - 1 = K.
Was ist mit dem zweiten df-Wert, der im F-Test erscheint? Dieser bezieht sich immer auf die Freiheitsgrade, die mit den Residuen verbunden sind. Man kann sich dies auch in Form von Parametern vorstellen. Allerdings geschieht das auf eine etwas kontra-intuitive Weise. Stellen Sie sich das folgendermaßen vor. Nehmen wir an, dass die Gesamtzahl der Beobachtungen in der gesamten Studie N beträgt. Wenn Sie jeden dieser N Werte perfekt beschreiben wollten, müssten Sie dies mit N Zahlen tun. Wenn Sie ein Regressionsmodell erstellen, legen Sie damit eigentlich nur fest, dass einige der Zahlen die Daten perfekt beschreiben müssen. Wenn Ihr Modell K Prädiktoren und ein Interzept hat, dann haben Sie K + 1 Zahlen verwendet. Ohne sich die Mühe zu machen, genau herauszufinden, wie dies geschehen würde, wie viele weitere Zahlen werden Ihrer Meinung nach benötigt, um ein Regressionsmodell mit K + 1 Parametern in eine perfekte Neubeschreibung der Rohdaten zu verwandeln? Gut gemacht, wenn Sie sich gedacht haben, dass (K + 1) + (N - K - 1) = N ist und die Antwort daher N - K - 1 lauten müsste. Das ist genau richtig. Im Prinzip können Sie sich ein absurd kompliziertes Regressionsmodell vorstellen, das für jeden einzelnen Datenpunkt einen Parameter enthält, und das natürlich eine perfekte Beschreibung der Daten liefern würde. Dieses Modell würde insgesamt N Parameter enthalten, aber wir interessieren uns für die Differenz zwischen der Anzahl der Parameter, die zur Beschreibung dieses vollständigen Modells erforderlich sind (d. h. N), und der Anzahl der Parameter, die von dem einfacheren Regressionsmodell verwendet werden, an dem wir eigentlich interessiert sind (d. h., K + 1), so dass der zweite Freiheitsgrad im F-Test df2 = N - K - 1 ist, wobei K die Anzahl der Prädiktoren (im Regressionsmodell) oder die Anzahl der Kontraste (in einer ANOVA) ist. In dem oben genannten Beispiel gibt es N = 18 Beobachtungen im Datensatz und K + 1 = 4 Regressionskoeffizienten, die mit dem ANOVA-Modell verbunden sind, so dass die Anzahl der Freiheitsgrade für die Residuen df2 = 18 - 4 = 14 beträgt.