Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft

Voraussetzungen, um eine ANOVA durchführen zu können

Wie jeder statistische Test beruht auch die Varianzanalyse auf einigen Annahmen über die Daten, insbesondere über die Residuen. Es gibt drei wichtige Annahmen, die Sie kennen müssen: Normalverteilung, Varianzhomogenität und Unabhängigkeit.

Wenn Sie sich an den Abschnitt Ein Modell für die Daten und die Bedeutung von *F* erinnern, den Sie hoffentlich zumindest überflogen haben, habe ich die statistischen Modelle, welche der ANOVA zu Grunde liegen, auf folgende Weise beschrieben:

H₀: Y_ik = µ + ϵ_ik

H₁: Y_ik = µ_k + ϵ_ik

In diesen Gleichungen bezieht sich μ auf einen einzelnen Gesamtmittelwert in der Grundgesamtheit, der für alle Gruppen gleich ist, und μ_k ist der Mittelwert für die k-te Gruppe in der Grundgesamtheit. Bis zu diesem Punkt waren wir vor allem daran interessiert, ob unsere Daten am besten in Form des Gesamtmittelwerts (der Nullhypothese) oder in Bezug auf verschiedene gruppenspezifische Mittelwerte (die Alternativhypothese) beschrieben werden können. Das macht natürlich Sinn, denn das ist eigentlich die wichtige Forschungsfrage! Alle unsere Testverfahren beruhen jedoch implizit auf einer bestimmten Annahme über die Residuen, ε_ik, nämlich, dass

ϵ_ik ~ Normal(0, σ²)

Keine der Gleichungen funktioniert ohne diesen Bestandteil. Oder, um genau zu sein, Sie können immer noch alle Berechnungen durchführen und Sie erhalten eine F-Statistik, aber Sie haben keine Garantie, dass diese F-Statistik tatsächlich misst, was Sie denken, dass sie misst, und so könnten alle Schlussfolgerungen, die Sie auf der Grundlage des F-Tests ziehen könnten, falsch sein.

Wie überprüfen wir also, ob die Annahme über die Residuen richtig ist? Nun, wie ich oben angedeutet habe, gibt es drei verschiedene Behauptungen, die in dieser einen Aussage vergraben sind, und wir werden sie nacheinander betrachten.

Varianzhomogenität. Beachten Sie, dass wir nur einen Wert für die Standardabweichung in der Grundgesamtheit (d. h. σ) haben, anstatt zuzulassen, dass jede Gruppe ihren eigenen Wert hat (d. h. σ_k). Dies wird als Annahme der Varianzhomogenität (manchmal auch als Homoskedastizität) bezeichnet. ANOVA geht davon aus, dass die Standardabweichung in der Grundgesamtheit für alle Gruppen gleich ist. Wir werden darüber ausführlich im Abschnitt Überprüfen der Annahme der Varianzhomogenität sprechen.
Normalverteilung. Es wird angenommen, dass die Residuen normalverteilt sind. Wie wir im Abschnitt Überprüfen der Normalverteilung in einer Stichprobe gesehen haben, können wir dies durch das Betrachten von Q-Q-Diagrammen (oder das Durchführen eines Shapiro-Wilk-Tests) beurteilen. Im Zusammenhang mit einer ANOVA werde ich dies im Abschnitt Überprüfen der Annahme einer Normalverteilung näher erläutern.
Unabhängigkeit. Die Unabhängigkeitsannahme ist etwas schwieriger. Was es im Grunde bedeutet, ist, dass die Kenntnis eines Residuums nichts über andere Residuen aussagt. Von allen ϵ_ik-Werten wird angenommen, dass sie ohne „Berücksichtigung“ oder „Beziehung zu“ den anderen erzeugt wurden. Es gibt keinen offensichtlichen oder einfachen Weg, dies zu testen, aber es gibt einige Situationen, die klare Verstöße dagegen darstellen. Wenn Sie beispielsweise ein Messwiederholungsdesign haben, bei dem jeder Teilnehmer Ihrer Studie in mehr als einer Bedingung auftritt, dann verletzt dies die Annahme der Unabhängigkeit. In diesem Fall gibt es eine besondere Beziehung zwischen einigen Beobachtungen, nämlich denen, die von derselben Person stammen! In diesem Fall müssen Sie eine ANOVA mit Messwiederholung verwenden (siehe Abschnitt Einfaktorielle ANOVA mit Messwiederholung).

Überprüfen der Annahme der Varianzhomogenität

Es gibt mehr als einen Weg, um die Annahme der Varianzhomogenität zu testen. Der dafür in der Literatur am häufigsten verwendete Test ist der Levene-Test (Levene, 1960) und der eng verwandte Brown-Forsythe-Test (Brown & Forsythe, 1974).

Unabhängig davon, ob Sie den (Standard-)Levene-Test oder den Brown-Forsythe-Test durchführen, wird die Teststatistik, die manchmal mit F, aber manchmal mit W bezeichnet wird, genauso berechnet wie die F -Statistik für die reguläre ANOVA, indem einfach ein Z_ik anstelle von Y_ik verwendet wird. In Anbetracht dessen können wir uns nun ansehen, wie der Test in jamovi durchgeführt wird.

Der Levene-Test ist erschreckend einfach. Angenommen, wir haben unsere Ergebnisvariable Y_ik. Alles, was wir tun, ist eine neue Variable zu definieren, die ich Z_ik nennen werde und welche die absoluten Abweichungen vom Gruppenmittelwert enthält

Z_ik = Y_ik - Ȳ_k

Was nützt uns das? Nun, nehmen wir uns einen Moment Zeit, um darüber nachzudenken, was Z_ik eigentlich ist und was wir zu testen versuchen. Der Wert von Z_ik ist ein Maß dafür, wie die i-te Beobachtung in der k-ten Gruppe von ihrem Gruppenmittelwert abweicht. Und unsere Nullhypothese ist, dass alle Gruppen die gleiche Varianz, d.h. die gleichen Gesamtabweichungen von den Gruppenmitteln, haben! Die Nullhypothese in einem Levene-Test ist also, dass die Mittelwerte von Z für alle Gruppen in der Grundgesamtheit identisch sind. Was wir jetzt brauchen, ist ein statistischer Test der Nullhypothese, dass alle Gruppenmittel identisch sind. Wo haben wir das schon einmal gesehen? Oh richtig, das ist es, was ANOVA ist, und was der Levene-Test tut: Eine ANOVA für die neue Variable Z_ik durchzuführen.

Was ist mit dem Brown-Forsythe-Test? Macht er irgendwas besonders anders? Nein. Die einzige Änderung gegenüber dem Levene-Test besteht darin, dass er die transformierte Variable Z etwas anders konstruiert, indem er Abweichungen von den Medianen der Gruppen anstelle von Abweichungen von den Mittelwerten der Gruppen verwendet. Das heißt, für den Brown-Forsythe-Test

Z_ik = Y_ik - median_k(Y)

wobei Md_k(Y) der Median für die Gruppe k ist.

Durchführen des Levene-Tests in jamovi

Okay, und wie führen wir den Levene-Test durch? Eigentlich ganz einfach - unter der Option ANOVA → Assumption Checks klicken Sie einfach auf die Homogeneity tests-Checkbox. Wenn wir uns die in Abb. 134 angezeigte Ausgabe ansehen, sehen wir, dass der Test nicht signifikant ist (F(2,15) = 1,45, p = 0,266), es sieht also so aus, als ob die Annahme der Homogenität der Varianz erfüllt ist. Doch der Schein kann trügen! Wenn Ihr Stichprobenumfang groß ist, kann der Levene-Test einen signifikanten Effekt aufzeigen (d. h. p < 0,05), selbst wenn die Annahme der Varianzhomogenität nicht in einem Ausmaß verletzt wird, das die Robustheit der ANOVA beeinträchtigt. Dies war der Punkt, den George Box in dem obigen Zitat ansprach. Ähnlich verhält es sich, wenn Ihre Stichprobengröße recht klein ist, dann könnte die Annahme der Varianzhomogenität nicht erfüllt sein, obwohl der Levene-Test nicht signifikant ist (d. h. p > 0,05). Das bedeutet, dass Sie neben jedem statistischen Test auf Erfüllung der Annahme immer auch die Standardabweichung um die Mittelwerte für jede Gruppe / Kategorie in der Analyse darstellen sollten, um zu sehen, ob sie ziemlich ähnlich aussehen (d. h. Varianzhomogenität) oder nicht.

``Levene test``-Ausgabe für die ``One-Way ANOVA`` in jamovi — Abb. 134 `Levene test`-Ausgabe für die `One-Way ANOVA` in jamovi

Verletzung der Annahme der Varianzhomogenität

In unserem Beispiel hat sich die Annahme der Varianzhomogenität als gesichert herausgestellt: Der Levene-Test war nicht signifikant, sodass wir uns wahrscheinlich keine Sorgen machen müssen (wir sollten uns trotzdem zusätzlich das Diagramm der Standardabweichungen in den verschiedenen Gruppen ansehen). Im wirklichen Leben haben wir nicht immer so viel Glück. Wie retten wir unsere ANOVA, wenn die Annahme der Varianzhomogenität verletzt wird? Wenn Sie sich an unsere Diskussion bei den t-Tests erinnern, haben wir dieses Problem schon einmal gesehen. Der t-Test nach Student geht von gleichen Varianzen aus, daher bestand die Lösung darin, den t-Test nach Welch zu verwenden, wenn dies nicht der Fall war. Tatsächlich zeigte Welch (1951) auch, wie dieses Problem auch für die ANOVA gelöst werden kann (der einfaktoriellen ANOVA nach Welch). Es ist in jamovi innerhalb der One-Way ANOVA-Analyse implementiert. Dieser spezielle Analyseansatz erlaubt das Durchführen einer ANOVA mit nur einem Faktor. Um die ANOVA nach Welch für unser Beispiel auszuführen, würden wir die Analyse ANOVA → One-Way ANOVA in jamovi auswählen, die Variablen wir bei der (gewöhnlichen) ANOVA zuvor zuweisen und dann die Option Don't assume equal (Welch’s) setzen (wie in Abb. 135 gezeigt).

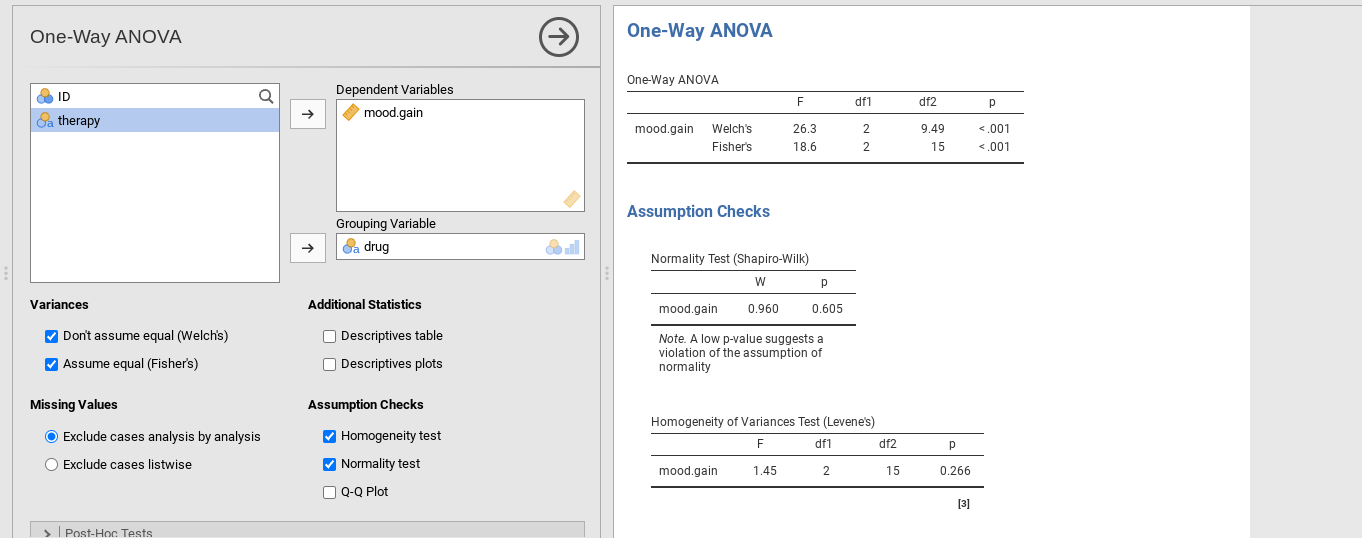
Abb. 135 ANOVA nach Welch als Teil der einfaktoriellen ANOVA in jamovi

Um zu verstehen, was hier passiert, vergleichen wir diese Zahlen mit denen, die wir zuvor im Abschnitt Durchführen einer ANOVA in jamovi erhalten haben, nämlich: F(2,15) = 18,611, p = 0,00009. Wie in Abb. 135 zu sehen ist, werden diese Werte auch in der One-Way ANOVA-Tabelle angezeigt (in der Zeile, die mit Fisher's beginnt), wenn die Checkbox Assume equal (Fisher's) gesetzt wird.

Ursprünglich lieferte uns unsere ANOVA das Ergebnis F(2,15) = 18,6, während die ANOVA nach Welch uns F(2, 9,49) = 26,32 lieferte. Mit anderen Worten, der Welch-Test hat die Freiheitsgrade innerhalb der Gruppen von 15 auf 9,49 reduziert und den F-Wert von 18,6 auf 26,32 erhöht.

Überprüfen der Annahme einer Normalverteilung

Das Überprüfen der Annahme einer Normalverteilung ist relativ einfach. Das meiste, was Sie wissen müssen, haben wir im Abschnitt Überprüfen der Normalverteilung in einer Stichprobe behandelt. Das Einzige, was wir wirklich tun müssen, ist, ein Q-Q-Diagramm zu zeichnen und, falls vorhanden, zusätzlich den Shapiro-Wilk-Test durchzuführen. Die Darstellung im Q-Q-Diagramm wird in Abb. 136 gezeigt und sieht aus als ob die Daten normalverteilt sind. Wenn der Shapiro-Wilk-Test nicht signifikant ist (d. h. p > 0,05), bedeutet dies, dass die Annahme der Normalverteilung nicht verletzt ist. Wie beim Levene-Test kann jedoch auch ein signifikanter Shapiro-Wilk-Test bei einer großen Stichprobengröße ein falsches positives Ergebnis sein, bei dem die Annahme der Normalverteilung nicht in einem für die Analyse problematischen Sinne verletzt wird. In ähnlicher Weise kann eine sehr kleine Stichprobe zu falsch negativen Ergebnissen führen. Deshalb ist eine visuelle Inspektion des Q-Q-Diagrammen wichtig.

Neben dem Überprüfen des Q-Q-Diagramms auf Abweichungen von der Normalverteilung zeigt der Shapiro-Wilk-Test für unsere Daten einen nicht signifikanten Effekt, mit p = 0,6053 (siehe Abb. 135). Dies stützt also den visuellen Eindruck aus dem Q-Q-Diagramm; beide Prüfungen ergeben keinen Hinweis auf eine Verletzung der Annahme einer Normalverteilung.

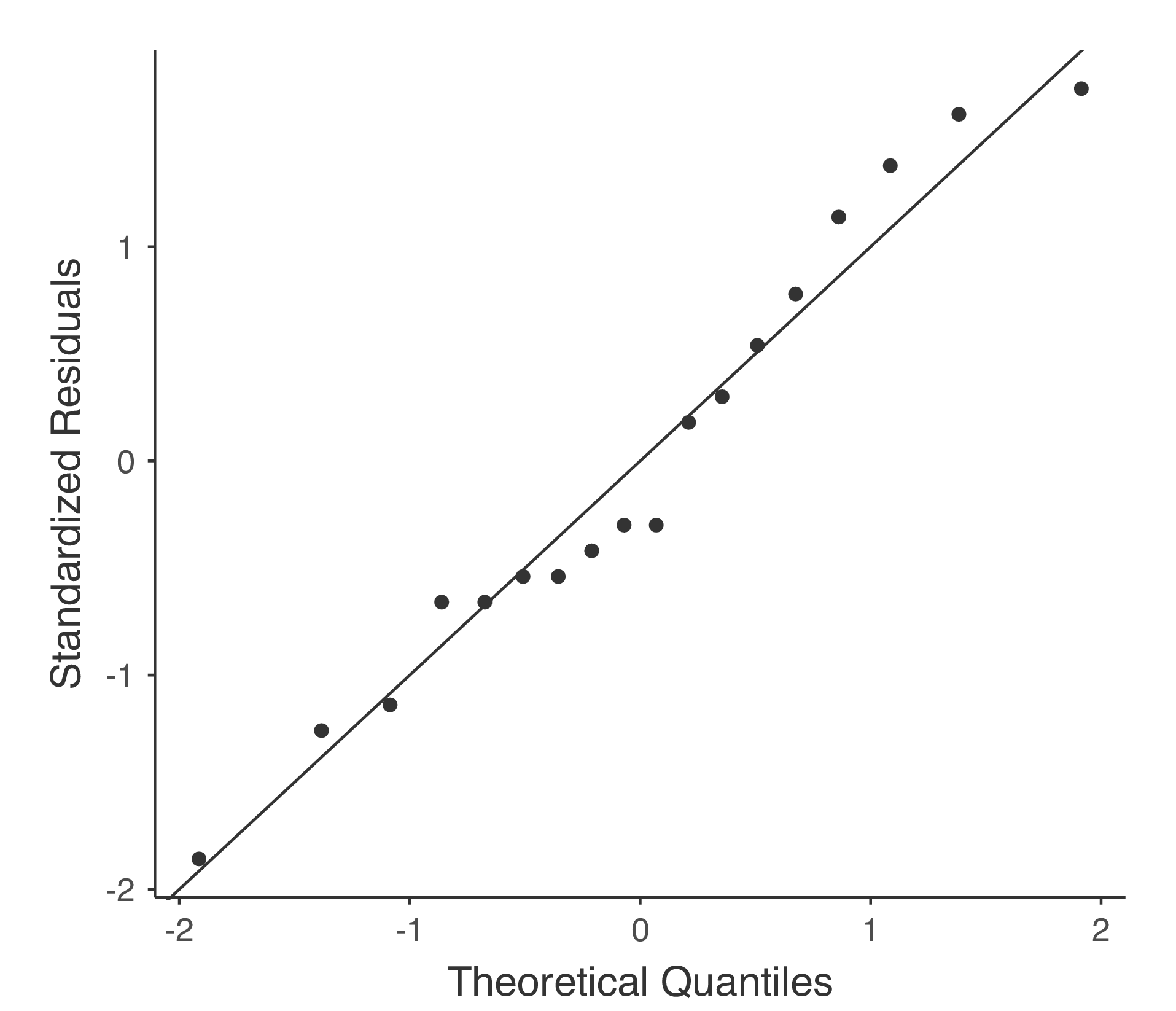
Q-Q-Diagramm erstellt mit Option ``QQ-plot`` innerhalb der ``One-Way ANOVA`` aus jamovi — Abb. 136 Q-Q-Diagramm erstellt mit Option `QQ-plot` innerhalb der `One-Way ANOVA` aus jamovi

Verletzungen der Annahme der Normalverteilung

Nachdem wir nun gesehen haben, wie man auf Normalverteilung prüft, stellt sich natürlich die Frage, was wir tun können, um Verletzungen der Normalverteilung zu beheben. Im Zusammenhang mit einer einfaktoriellen ANOVA besteht die einfachste Lösung wahrscheinlich darin, zu einem nicht-parametrischen Test zu wechseln (d.h. einem Test, der nicht auf einer bestimmten Annahme über die Art der beteiligten Verteilung beruht). Wir haben nichtparametrische Tests bereits im Abschnitt Prüfen nicht-normalverteilter Daten mit dem Wilcoxon-Test kennengelernt. Wenn Sie nur zwei Gruppen haben, ist der Mann-Whitney- oder der Wilcoxon-Test die nichtparametrische Alternative, die Sie brauchen. Wenn Sie drei oder mehr Gruppen haben, können Sie den Kruskal-Wallis-Rangsummentest (Kruskal & Wallis, 1952) verwenden. Das ist der Test, über den wir als Nächstes sprechen werden.

Der Kruskal-Wallis-Test ist der ANOVA überraschend ähnlich. In der ANOVA haben wir mit Y_ik begonnen, dem Wert der Ergebnisvariablen für die i-te Person in der k-ten Gruppe. Für den Kruskal-Wallis-Test ordnen wir alle diese Y_ik-Werte zu einer Rangfolge und führen unsere Analyse mit den Rangdaten durch.

Lassen Sie uns also R_ik auf den Rang beziehen, der dem i-ten Mitglied der k-ten Gruppe gegeben wurde. Berechnen wir nun R̄_k, den durchschnittlichen Rang, der den Beobachtungen in der k-ten Gruppe gegeben wird:

\[\bar{R}_k = \frac{1}{N_K} \sum_{i} R_{ik}\]

und berechnen wir außerdem R̄, den mittleren Rang über alle Messungen

\[\bar{R} = \frac{1}{N} \sum_{i} \sum_{k} R_{ik}\]

Nachdem wir dies getan haben, können wir die quadrierten Abweichungen von R̄, dem Mittelwert der Ränge über alle Messungen, berechnen. Wenn wir dies für die einzelnen Werte tun, d.h. wenn wir (R_ik – R̄)² berechnen, haben wir ein „nichtparametrisches“ Maß dafür, wie weit die ik-te Beobachtung vom großen mittleren Rang abweicht. Wenn wir die quadrierte Abweichung der Gruppenmittelwerte vom Mittelwerten der Ränge über alle Messungen berechnen, d.h. wenn wir (R̄_k – R̄)² berechnen, dann haben wir ein nichtparametrisches Maß dafür, wie stark der Mittelwerten der Ränge der Gruppe k vom Mittelwerten der Ränge über alle Messungen abweicht. In diesem Sinne folgen wir der gleichen Logik wie bei ANOVA und definieren die Quadratsummen der Ränge, ähnlich wie wir es zuvor getan haben. Erstens haben wir unsere „Gesamtquadratsumme der Ränge“

\[\mbox{RSS}_{tot} = \sum_k \sum_i ( R_{ik} - \bar{R} )^2\]

und wir können die „Quadratsumme der Ränge zwischen den Gruppen“ definieren als

\[\begin{split}\begin{array}{rcl} \mbox{RSS}_{b} &=& \sum_k \sum_i ( \bar{R}_k - \bar{R} )^2 \\ &=& \sum_k N_k ( \bar{R}_k - \bar{R} )^2 \end{array}\end{split}\]

Wenn die Nullhypothese wahr ist und es überhaupt keine wahren Gruppenunterschiede gibt, würden wir erwarten, dass die Quadratsumme der Ränge zwischen den Gruppen RSS_b sehr klein ist, viel kleiner als die Gesamtquadratsumme der Ränge RSS: sub:tot. Qualitativ ist dies ziemlich dasselbe wie das, was wir beim Erstellen der F-Statistik innerhalb der ANOVA gemacht haben. Aus technischen Gründen wird die Kruskal-Wallis-Teststatistik, die normalerweise als K bezeichnet wird, jedoch etwas anders konstruiert,

\[K = (N - 1) \times \frac{\mbox{RSS}_b}{\mbox{RSS}_{tot}}\]

und wenn die Nullhypothese wahr ist, dann ist die Stichprobenverteilung von K ungefähr χ²-verteilt mit G - 1 Freiheitsgraden (wobei G die Anzahl der Gruppen ist). Je größer der Wert von K, desto weniger konsistent sind die Daten mit der Nullhypothese, es handelt sich also um einen einseitigen Test. Wir lehnen H₀ ab, wenn K ausreichend groß ist.

Die Beschreibung im vorherigen Abschnitt veranschaulicht die Logik hinter dem Kruskal-Wallis-Test. Auf konzeptioneller Ebene ist dies der richtige Weg, um darüber nachzudenken, wie der Test funktioniert. Aus rein mathematischer Sicht ist es jedoch unnötig kompliziert. Ich werde Ihnen die Herleitung nicht zeigen, aber wir können eine algebraische Spielerei verwenden,[1] um zu zeigen, dass die Gleichung für K umgeschrieben werden kann als

\[K = \frac{12}{N(N-1)} \sum_k N_k {\bar{R}_k}^2 - 3(N+1)\]

Es ist diese letzte Gleichung, die Sie manchmal für das Berechnen von K sehen. Sie ist viel einfacher zu berechnen als die Version, die ich im vorherigen Abschnitt beschrieben habe. Aber das ist für uns eigentlich bedeutungslos und es ist wahrscheinlich am besten, sich K so vorzustellen, wie ich es zuvor beschrieben habe: als Analogon der ANOVA basierend auf Rängen. Denken Sie jedoch daran, dass die berechnete Teststatistik am Ende etwas anders aussieht als die, welche wir für unsere ursprüngliche ANOVA verwendet haben.

Aber warten Sie, es gibt noch mehr! Die Geschichte, die ich bisher erzählt habe, ist nur dann wirklich wahr, wenn es keine verbundenen Ränge in den Rohdaten gibt. Das heißt, wenn es keine zwei Beobachtungen gibt, die genau den gleichen Wert haben. Wenn es verbundene Ränge gibt, dann müssen wir noch einen Korrekturfaktor für diese Berechnungen einführen. An diesem Punkt gehe ich davon aus, dass selbst der fleißigste Leser aufgehört hat, sich darum zu kümmern (oder sich zumindest die Meinung gebildet hat, dass der Korrekturfaktor für verbundene Ränge etwas ist, das keine unmittelbare Aufmerksamkeit erfordert). Also werde ich Ihnen sehr schnell sagen, wie es berechnet wird, und die mühsamen Details, warum es so gemacht wird, weglassen. Angenommen, wir erstellen eine Häufigkeitstabelle für die Rohdaten und lassen f_j die Anzahl der Beobachtungen sein, die den j-ten eindeutigen Wert haben. Das mag etwas abstrakt klingen, also hier ist ein konkretes Beispiel aus der Häufigkeitstabelle von mood.gain aus dem Datensatz clinicaltrial:

0.1	0.2	0.3	0.4	0.5	0.6	0.8	0.9	1.1	1.2	1.3	1.4	1.7	1.8
1	1	2	1	1	2	1	1	1	1	2	2	1	1

Wenn Sie sich diese Tabelle ansehen, beachten Sie, dass der dritte Eintrag in der Häufigkeitstabelle den Wert 2 hat. Da dies einem „Stimmungsgewinn“ von 0,3 entspricht, sagt uns diese Tabelle, dass sich die Stimmung zweier Personen um 0,3 erhöht hat. Genauer gesagt, in der mathematischen Notation, die ich oben eingeführt habe, sagt uns dies, dass f₃ = 2. Yay. Nun, da wir das wissen, lässt sich der Korrekturfaktor für vernundene Ränge (tie correction factor, TCF) wie folgt berechnen:

\[\mbox{TCF} = 1 - \frac{\sum_j {f_j}^3 - f_j}{N^3 - N}\]

Wir erhalten einen Wert für die Kruskal-Wallis-Statistik, der für verbundene Ränge korrigiert ist, indem der Wert von K durch diesen Faktor dividiert wird. jamovi berechnet diese Version, die für verbundene Ränge korrigiert. Und endlich sind wir mit der Theorie des Kruskal-Wallis-Tests fertig. Ich bin sicher, Sie sind alle erleichtert, dass ich Sie von der Existenzangst befreit habe, die dadurch entsteht, dass Sie nicht wissen, wie man den Korrekturfaktor für verbundene Ränge beim Kruskal-Wallis-Test berechnet…

Durchführen des Kruskal-Wallis-Tests in jamovi

Obwohl es nicht ganz einfach war, zu verstehen, wie der Kruskal-Wallis-Test funktioniert, stellt sich heraus, dass das Durchführen des Tests ziemlich reibungslos funktioniert. jamovi implementiert diese Analyse als Teil der ANOVA-Analysen unter Non-Parametric - One-Way ANOVA (Kruskall-Wallis). Oft haben Sie Daten wie die aus dem Datensatz clinicaltrial, mit einer Ergebnisvariable wie mood.gain und einer Gruppierungsvariable wie drug. Mit solchen Daten können Sie die Analyse in jamovi einfach durchführen. Sie ergibt ein Kruskal-Wallis χ² = 12,076, df = 2, p = 0,00239, wie in Abb. 137 gezeigt.

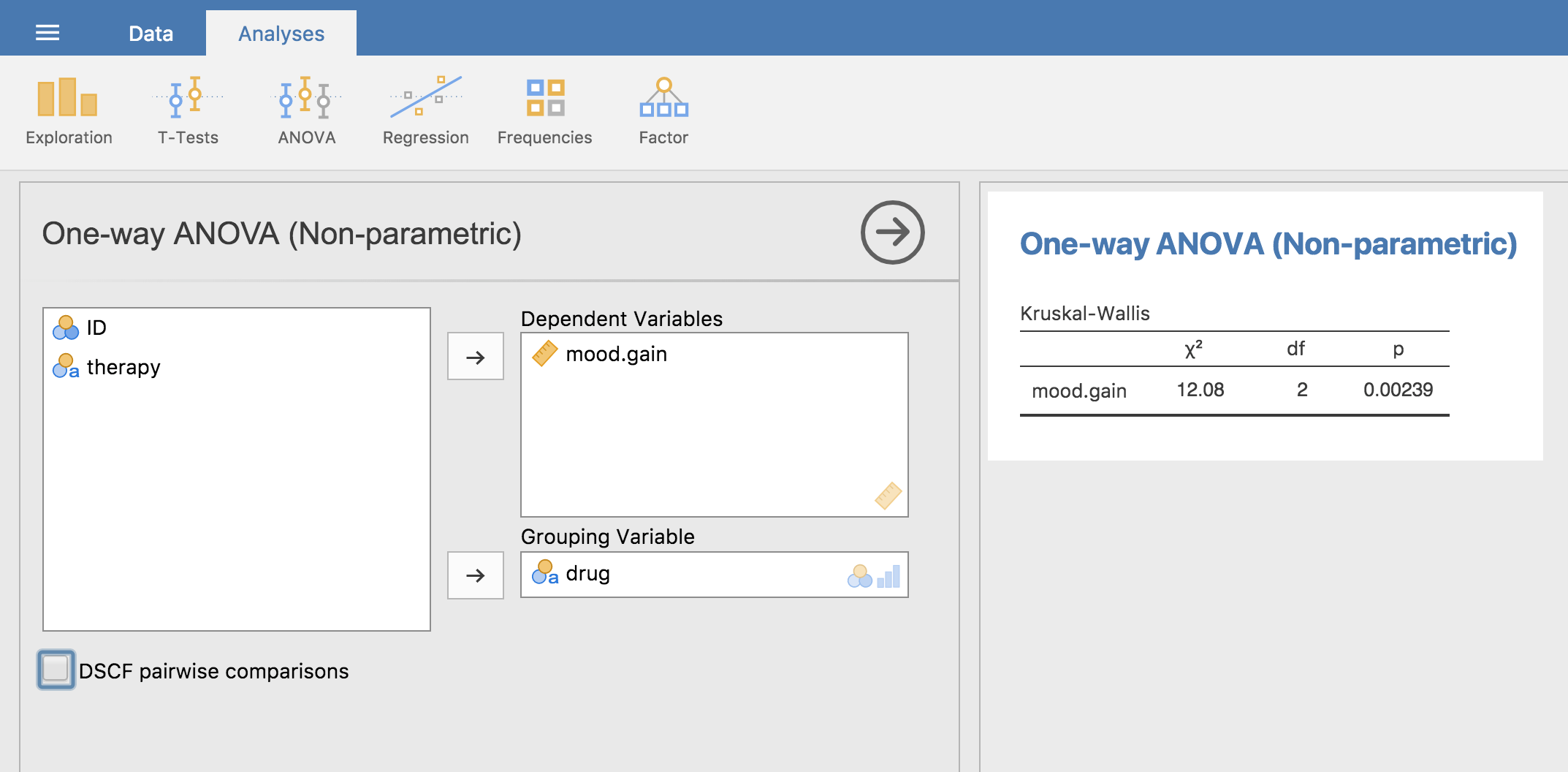
Nicht-parametrische ``One-Way ANOVA (Kruskal-Wallis)`` in jamovi — Abb. 137 Nicht-parametrische `One-Way ANOVA (Kruskal-Wallis)` in jamovi