Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft
Der t-Test für gepaarte Stichproben
Unabhängig davon, ob es sich um den t-Test nach Student oder den t-Test nach Welch handelt, ist ein t-Test für unabhängige Stichproben dafür gedacht, in einer Situation verwendet zu werden, in der man zwei Stichproben hat, die unabhängig voneinander sind. Diese Situation tritt natürlich auf, wenn die Teilnehmer nach dem Zufallsprinzip einer von zwei Versuchsbedingungen zugewiesen werden, aber sie bietet eine sehr schlechte Annäherung an andere Arten von Forschungsdesigns. Insbesondere ein Versuchsplan mit wiederholten Messungen, bei dem jeder Teilnehmer (in Bezug auf dieselbe Ergebnisvariable) in beiden Versuchsbedingungen gemessen wird, eignet sich nicht für die Analyse mit dem t-Test für unabhängige Stichproben. Wir könnten uns zum Beispiel dafür interessieren, ob das Hören von Musik die Kapazität des Arbeitsgedächtnisses von Personen verringert. Zu diesem Zweck messen wir die Arbeitsgedächtniskapazität jeder Person unter zwei Bedingungen: mit Musik und ohne Musik. In einem Versuchsplan wie diesem[1] erscheint jeder Teilnehmer in beiden Gruppen. Dies erfordert eine andere Herangehensweise an das Problem, nämlich die Verwendung des t-Tests für gepaarte Stichproben.
Die Daten
Der Datensatz, den wir dieses Mal verwenden, stammt aus der Klasse von Dr. Chico.[2] In seiner Klasse schreiben die Studenten zwei Examen, eins zu Beginn des Semesters und eins später im Semester. Sein Kurs ist eher schwierig, und die meisten Studenten empfinden ihn als äußerst herausfordernd. Er argumentiert jedoch, dass die Studierenden durch schwierige Examen ermutigt werden, härter zu arbeiten. Seine Theorie ist, dass das erste Examen eine Art „Weckruf“ für die Studierenden ist. Wenn sie merken, wie schwierig der Kurs wirklich ist, werden sie sich bei der zweiten Prüfung mehr anstrengen und eine bessere Note erzielen. Hat er Recht? Um dies zu überprüfen, öffnen wir den Datensatz chico in jamovi. Diesmal leistet jamovi beim Importieren gute Arbeit, indem es die Skalenniveaus korrekt zuordnet. Der chico-Datensatz enthält drei Variablen: eine id-Variable, die die einzelnen Studenten identifiziert, die grade_test1-Variable, mit der Note für das erste Examen, und die grade_test2-Variable, mit der Note für das zweite Examen.
Aus der jamovi-Datentabelle geht hervor, dass der Kurs sehr schwer ist (die meisten Noten liegen zwischen 50 % und 60 %), aber es sieht so aus, als ob eine Verbesserung vom ersten zum zweiten Test zu verzeichnen ist.
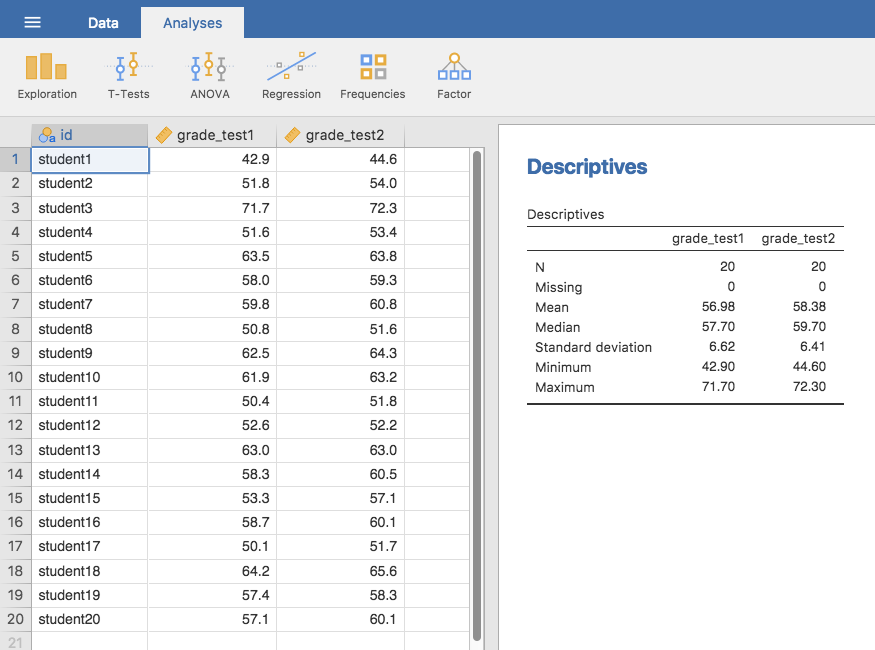
Abb. 94 Deskriptivstatistik für die Variablen mit den zwei Examensnoten aus dem Datensatz chico
Ein kurzer Blick auf die deskriptive Statistik in Abb. 94 zeigt, dass dieser Eindruck zu stimmen scheint. Über alle 20 Schüler hinweg liegt die Durchschnittsnote für den ersten Test bei 57 %, steigt aber zum zweiten Test auf 58 % an. Wenn man allerdings bedenkt, dass die Standardabweichungen bei 6,6 % abzw. 6,4 % liegen, bekommt man den Eindruck, dass die Verbesserung vielleicht nur illusorisch ist, d.h. eine zufällige Variation. Dieser Eindruck wird noch verstärkt, wenn man sich die Mittelwerte und Konfidenzintervalle in Abb. 95 (links) ansieht. Würde man sich allein auf diese Grafik verlassen und sich die Breite der Konfidenzintervalle ansehen, wäre man geneigt zu glauben, dass die Verbesserung der Schülerleistungen reiner Zufall ist.
Abb. 95 Mittelwert der Noten für Test 1 und Test 2, mit den zugehörigen 95%-Konfidenzintervallen (links). Streudiagramm mit den Einzelnoten für Test 1 und Test 2 (Mitte). Histogramm, das die Verbesserung der einzelnen Schüler in Dr. Chicos Klasse zeigt (rechts). Im rechten Teil ist zu erkennen, dass fast die gesamte Verteilung über Null liegt: die überwiegende Mehrheit der Schüler hat ihre Leistungen vom ersten zum zweiten Test verbessert.
Dieser Eindruck ist jedoch falsch. Um zu sehen, warum das so ist, sehen Sie sich das Streudiagramm der Noten für Examen 1 im Vergleich zu den Noten für Examen 2 an, das in Abb. 95 (Mitte) dargestellt ist. In diesem Diagramm entspricht jeder Punkt den beiden Noten für einen bestimmten Schüler. Wenn die Note für Examen 1 (x Koordinate) gleich der Note für Examen 2 (y Koordinate) ist, dann liegt der Punkt auf der Diagonalen. Punkte, die oberhalb der Linie liegen, sind die Schüler, die im zweiten Test besser abgeschnitten haben. Fast alle Datenpunkte befinden sich oberhalb der diagonalen Linie: Fast alle Schüler scheinen ihre Note verbessert zu haben, wenn auch nur um einen kleinen Betrag. Dies deutet darauf hin, dass wir uns die Verbesserung jedes Schülers von einem Examen zum nächsten ansehen und diese Verbesserung als unsere Rohdaten behandeln sollten. Um dies zu tun, müssen wir eine neue berechnete Variable improvement erstellen und sie dem chico Datensatz hinzufügen. Der Ausdruck für das Berechnen der neuen Variable ist grade_test2 - grade_test1.
Nachdem wir diese neue Variable improvement berechnet haben, können wir ein Histogramm zeichnen, das die Verteilung dieser Verbesserungswerte zeigt, dargestellt in Abb. 95 (rechts). Aus dem Histogramm geht eindeutig hervor, dass hier eine echte Verbesserung vorliegt. Die überwiegende Mehrheit der Schüler hat in Test 2 besser abgeschnitten als in Test 1, was sich darin zeigt, dass die Mehrheit der Werte im Histogramm über Null liegt.
Was macht der t-Test für gepaarte Stichproben?
Basierend auf unseren bisherigen Analyseschritten sollten wir uns überlegen, wie wir einen geeigneten t-Test konstruieren können. Eine Möglichkeit wäre, einen t-Test für unabhängige Stichproben durchzuführen, bei dem grade_test1 und grade_test2 als Variablen von Interesse verwendet werden. Dies ist jedoch eindeutig der falsche Weg, da der Test mit unabhängigen Stichproben t-test davon ausgeht, dass es keine Beziehung oder Abhängigkeit zwischen den beiden Stichproben gibt. Aufgrund der wiederholten Messungen ist dies jedoch eindeutig der Fall. Um die Sprache zu verwenden, die ich im letzten Abschnitt eingeführt habe: Wenn wir versuchen würden, einen t-Test für unabhängige Stichproben durchzuführen, würden wir die Unterschiede innerhalb der Probanden (an denen wir interessiert sind) mit der Variabilität zwischen den Probanden (an der wir nicht interessiert sind) miteinander vermischen (konfundieren).
Die Lösung des Problems ist hoffentlich offensichtlich, da wir die ganze harte Arbeit bereits im vorherigen Abschnitt erledigt haben. Anstatt einen t-Test für unabhängige Stichproben mit grade_test1 und grade_test2 durchzuführen, führen wir einen t-Test für eine Stichprobe mit der Variable für die Differenz innerhalb des Subjekts, improvement, durch. Um dies zu formalisieren: Wenn X:sub`i1` die Punktzahl ist, die der i-te Teilnehmer bei der ersten Variable erreicht hat, und X:sub`i2` die Punktzahl ist, die dieselbe Person bei der zweiten Variable erreicht hat, dann ist die Differenzpunktzahl:
Beachten Sie, dass der Differenzwert Variable 1 minus Variable 2 ist und nicht umgekehrt. Wenn wir also wollen, dass eine Verbesserung einer positiv bewerteten Differenz entspricht, wollen wir eigentlich, dass „Test 2“ unsere „Variable 1“ ist. Gleichermaßen würden wir sagen, dass µ:sub`D` = µ:sub`1` - µ:sub`2` der Populationsmittelwert für diese Differenzvariable ist. Um dies in einen Hypothesentest umzuwandeln, lautet unsere Nullhypothese, dass dieser Mittelwertunterschied gleich Null ist, und die Alternativhypothese, dass er es nicht ist
Wir gehen davon aus, dass es sich hier um einen zweiseitigen Test handelt. Dies ist mehr oder weniger identisch mit der Art und Weise, wie wir die Hypothesen für den t-Test mit einer Stichprobe beschrieben haben. Der einzige Unterschied besteht darin, dass der spezifische Wert, den die Nullhypothese vorhersagt, 0 ist. Daher ist auch unsere t-Statistik mehr oder weniger auf die gleiche Weise definiert. Wenn wir D̄ den Mittelwert der Differenzwerte bezeichnen lassen, dann
das ist
wobei \(\hat\sigma_D\) die Standardabweichung der Differenzwerte ist. Da es sich um einen gewöhnlichen t-Test mit einer Stichprobe handelt, der nichts Besonderes ist, sind die Freiheitsgrade immer noch N - 1. Und das war’s. Der t-Test für gepaarte Stichproben ist eigentlich gar kein neuer Test. Es handelt sich um einen t-Test mit einer Stichprobe, der jedoch auf die Differenz zwischen zwei Variablen angewendet wird. Er ist eigentlich sehr einfach. Der einzige Grund, warum er eine so lange Diskussion verdient, wie wir sie gerade geführt haben, ist, dass man in der Lage sein muss, zu erkennen, wann ein t-Test für gepaarte Stichproben angebracht ist, und zu verstehen, warum er besser ist als ein t-Test für unabhängige Stichproben.
Durchführen des Tests in jamovi
Wie führt man einen t-Test für gepaarte Stichproben in jamovi durch? Eine Möglichkeit besteht darin, den oben beschriebenen Prozess zu befolgen. Das heißt, Sie erstellen eine Variable difference und führen dann einen t-Test mit einer Stichprobe durch. Da wir bereits eine Variable mit dem Namen improvement erstellt haben, können wir das tun und sehen, welches Ergebnis wir erhalten (siehe Abb. 96).

Abb. 96 Die Ergebnisse zeigen einen t-Test mit paarweisen Differenzwerten
Die in Abb. 96 gezeigte Ausgabe ist (natürlich) genau so formatiert wie bei der One Sample T-Test Analyse (Abschnitt Der t-Test bei einer Stichprobe), und sie bestätigt unsere Intuition. Es gibt eine durchschnittliche Verbesserung von 1,4 % von Examen 1 zu Examen 2, und diese ist signifikant verschieden von 0 (t(19) = 6,48, p < 0,001).
Nehmen wir jedoch an, Sie wollen sich nicht die Mühe machen, eine neue Variable zu erstellen. Oder vielleicht wollen Sie einfach nur einen deutlichen Unterschied zwischen Tests mit einer Stichprobe und Tests mit gepaarten Stichproben machen. In diesem Fall können Sie die Analyse Paired Samples T-Test in jamovi verwenden und erhalten die in Abb. 97 angezeigten Ergebnisse.

Abb. 97 Ergebnisse eines t-Tests für gepaarte Stichproben. Vergleichen Sie es mit Abb. 96.
Die Zahlen sind identisch mit denen des Einstichprobentests, was sie natürlich auch sein müssen, da der t-Test für gepaarte Stichproben unter der Haube ein t-Test für eine Stichprobe ist.