Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft

Der McNemar-Test

Nehmen wir an, Sie wurden von der Australian Generic Political Party (AGPP) eingestellt. Eine Ihrer Aufgaben besteht darin, herauszufinden, wie wirksam die politische Werbung der AGPP ist. Also beschließen Sie, eine Stichprobe von N = 100 Personen zusammenzustellen und sie zu bitten, sich die AGPP-Werbung anzusehen. Bevor die Probanden die Werbung sehen, fragen Sie sie, ob sie beabsichtigen, für die AGPP zu stimmen, und dann, nachdem die Werbung gezeigt wurde, fragen Sie sie erneut, um zu sehen, ob jemand seine Meinung geändert hat. Wenn Sie in Ihrem Job gut sind, würden Sie natürlich noch eine ganze Menge anderer Dinge tun, aber konzentrieren wir uns nur auf dieses eine einfache Experiment. Eine Möglichkeit, Ihre Daten zu beschreiben, ist die folgende Kreuztabelle:

	Vorher	Nachher	Insgesamt
Ja	30	10	40
Nein	70	90	160
Insgesamt	100	100	200

Auf den ersten Blick könnte man meinen, dass sich diese Situation für den Pearson χ²-Unabhängigkeitstest eignet. Ein wenig Nachdenken zeigt jedoch, dass wir ein Problem haben. Wir haben 100 Teilnehmer, aber 200 Beobachtungen. Das liegt daran, dass jede Person sowohl in der Vorher-Spalte als auch in der Nachher-Spalte eine Antwort gegeben hat. Das bedeutet, dass die 200 Beobachtungen nicht unabhängig voneinander sind. Wenn Wähler A beim ersten Mal mit „Ja“ antwortet und Wähler B mit „Nein“, dann würde man erwarten, dass Wähler A beim zweiten Mal mit größerer Wahrscheinlichkeit mit „Ja“ antwortet als Wähler B! Dies hat zur Folge, dass der übliche χ²-Unabhängigkeitstest aufgrund der Verletzung der Unabhängigkeitsannahme keine vertrauenswürdigen Antworten liefern wird. Wenn dies eine wirklich ungewöhnliche Situation wäre, würde ich mir nicht die Mühe machen, Ihre Zeit damit zu verschwenden, darüber zu sprechen. Aber es ist überhaupt nicht ungewöhnlich. Es handelt sich um ein Standarddesign mit wiederholten Messungen, und leider kann keiner der Tests, die wir bisher betrachtet haben, damit umgehen.

Die Lösung des Problems wurde von McNemar (1947) veröffentlicht. Der Trick besteht darin, die Daten zunächst auf eine etwas andere Weise zu tabellieren:

	Vorher: Ja	Vorher: Nein	Insgesamt
Nachher: Ja	5	5	10
Nachher: Nein	25	65	90
Insgesamt	30	70	100

Dies sind genau die gleichen Daten, aber sie wurden so umgeschrieben, dass jeder unserer 100 Teilnehmer nur in einer Zelle erscheint. Da wir unsere Daten auf diese Weise umstrukturiert haben, ist die Unabhängigkeitsannahme nun erfüllt, und dies ist eine Kreuztabelle, die wir verwenden können, um eine χ²-(goodness-of-fit)-Statistik zu erstellen. Wie wir jedoch sehen werden, müssen wir dies auf eine etwas unübliche Weise tun. Um zu sehen, was vor sich geht, ist es hilfreich, die Einträge in unserer Tabelle ein wenig anders zu beschriften:

	Vorher: Ja	Vorher: Nein	Insgesamt
Nachher: Ja	a	b	a + b
Nachher: Nein	c	d	c + d
Insgesamt	a + c	b + d	n

Überlegen wir uns nun, was unsere Nullhypothese ist: Sie besagt, dass der „Vorher“-Test und der „Nachher“-Test den gleichen Anteil an Personen aufweisen, die behaupten „Ja, ich werde für die AGPP stimmen“. Aufgrund der Art und Weise, wie wir die Daten umgeschrieben haben, bedeutet dies, dass wir jetzt die Hypothese testen, dass die Zeilensummen und die Spaltensummen aus derselben Verteilung stammen. Die Nullhypothese des McNemar-Tests lautet also, dass „marginale Homogenität“ (Homogenität der Randsummen) vorliegt. Das heißt, die Zeilensummen und die Spaltensummen haben die gleiche Verteilung: P_a + P_b = P_a + P_c und ebenso P_c + P_d = P_b + P_d. Man beachte, dass dies bedeutet, dass die Nullhypothese tatsächlich zu P_b = P_cvereinfacht wird. Mit anderen Worten, für den McNemar-Test sind nur die Einträge außerhalb der Diagonalen in dieser Tabelle von Bedeutung (d.h. b und c). Nachdem wir dies festgestellt haben, unterscheidet sich der McNemar-Test auf marginale Homogenität nicht von einem gewöhnlichen χ²-Test. Nach der Anwendung der Yates-Korrektur wird unsere Teststatistik zu:

\[\chi^2 = \frac{(|b-c| - 0.5)^2}{b+c}\]

oder, um zu der Notation zurückzukehren, die wir zuvor in diesem Kapitel verwendet haben:

\[\chi^2 = \frac{(|O_{12}-O_{21}| - 0.5)^2}{O_{12} + O_{21}}\]

und diese Statistik hat eine (annähernde) χ²-Verteilung mit df = 1. Denken Sie jedoch daran, dass es sich wie bei den anderen χ²-Tests nur um eine Annäherung handelt, d. h. Sie müssen eine relativ große erwartete Zellzahl haben, damit der Test funktioniert.

Durchführen des McNemar-Tests in jamovi

Nachdem wir nun wissen, worum es beim McNemar-Test geht, können wir einen solchen Test durchführen. Der Datensatz agpp enthält die Rohdaten, von denen ich zuvor gesprochen habe. Er enthält drei Variablen, eine id Variable, die jeden Teilnehmer im Datensatz kennzeichnet (wir werden gleich sehen, warum das nützlich ist), eine response_before-Variable, die die Antwort der Person aufzeichnet, als ihr die Frage zum ersten Mal gestellt wurde, und eine response_after Variable, die die Antwort anzeigt, die sie gegeben hat, nachdem sie die Werbung gesehen hat. Beachten Sie, dass jeder Teilnehmer nur einmal in diesem Datensatz vorkommt. Gehen Sie zu Analyses → Frequencies → Contingency Tables → Paired Samples in jamovi, und verschieben Sie response_before in das Feld Rows und response_after in das Feld Columns. Sie erhalten dann eine Kreuztabelle im Ergebnisfenster, mit der Statistik für den McNemar-Test direkt darunter (wie in Abb. 80 gezeigt):

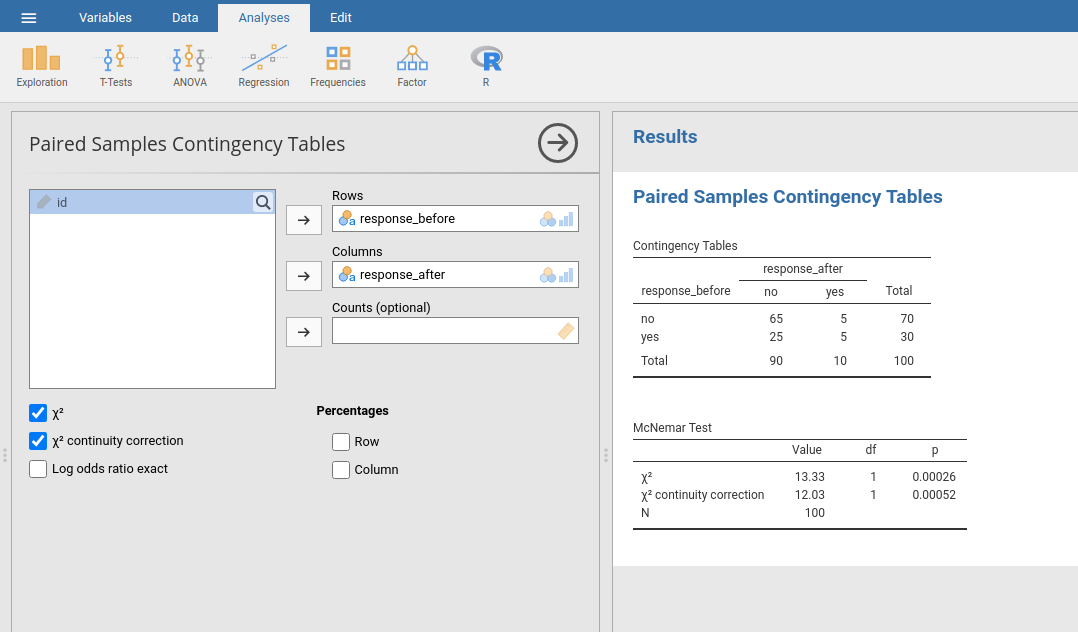
Abb. 80 Ergebnisausgabe des McNemar-Tests in jamovi

Und damit sind wir fertig. Wir haben gerade einen McNemar-Test durchgeführt, um festzustellen, ob die Leute nach der Werbung genauso wahrscheinlich für AGPP stimmen werden wie vorher. Der Test war signifikant (χ²(1) = 12,03, p < 0,001), was darauf hindeutet, dass dies nicht der Fall war. Und tatsächlich sieht es so aus, als hätten die Anzeigen einen negativen Effekt: Die Wahrscheinlichkeit, AGPP zu wählen, war geringer, nachdem die Menschen die Anzeigen gesehen hatten. Das verwundert nicht wirklich, wenn man die Qualität einer typischen politischen Werbung betrachtet.

Was ist der Unterschied zwischen McNemar und χ²-Unabhängigkeitstest?

Gehen wir noch einmal ganz an den Anfang des Kapitels zurück und betrachten wir noch einmal den cards-Datensatz. Wie Sie sich erinnern, ging es bei dem von mir beschriebenen Versuchsplan darum, dass die Personen zwei Entscheidungen treffen. Da wir Informationen über die erste Wahl und die zweite Wahl haben, die jeder getroffen hat, können wir die folgende Kreuztabelle erstellen, welche die erste Wahl mit der zweiten Wahl vergleicht.

          choice_2
choice_1   clubs diamonds hearts spades
  clubs       10        9     10      6
  diamonds    20        4     13     14
  hearts      20       18      3     23
  spades      18       13     15      4

Angenommen, ich möchte wissen, ob die Wahl, die Sie beim zweiten Mal treffen, von der Wahl abhängig ist, die Sie beim ersten Mal getroffen haben. In diesem Fall ist ein Unabhängigkeitstest nützlich, und wir wollen herausfinden, ob es eine Beziehung zwischen den Zeilen und Spalten dieser Tabelle gibt.

Oder nehmen wir an, ich möchte wissen, ob im Durchschnitt die Häufigkeit der Farbwahlen beim zweiten Mal anders ist, als beim ersten Mal. In diesem Fall möchte ich eigentlich wissen, ob sich die Zeilensummen von den Spaltensummen unterscheiden. In diesem Fall sollten wir den McNemar-Test verwenden.

Die verschiedenen Statistiken, die sich aus diesen unterschiedlichen Analysen ergeben, sind in Abb. 81 dargestellt. Beachten Sie, dass die Ergebnisse unterschiedlich sind, da es sich nicht um denselben Test handelt.

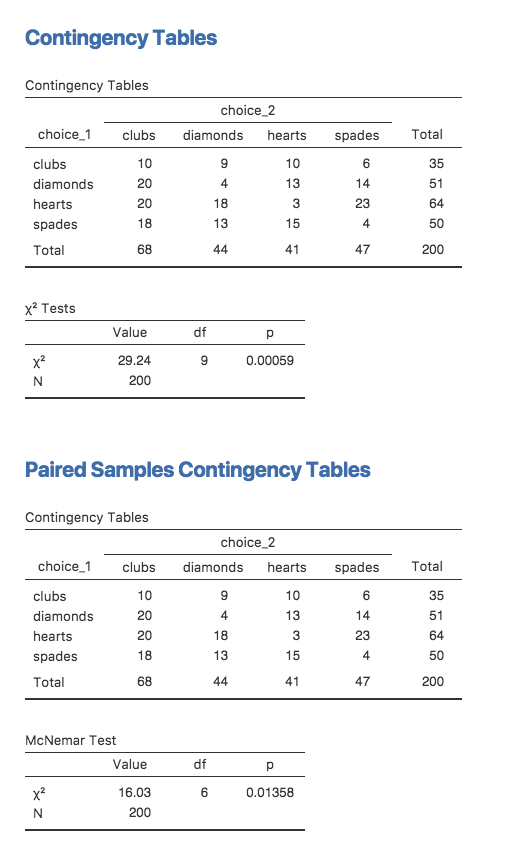
Abb. 81 Ergebnisausgabe für den χ²-Unabhängigkeitstest sowie für den McNemar-Test (gepaarte Stichproben) in jamovi