Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft

Der χ²-Anpassungstest

Der χ² (Chi-Quadrat)-Anpassungstest ist einer der ältesten Hypothesentests überhaupt. Er wurde von Karl Pearson (1900) erfunden, wobei später von Sir Ronald Fisher (1922a) einige Korrekturen vorgenommen wurden. Er prüft, ob eine beobachtete Häufigkeitsverteilung einer nominalen Variablen mit einer erwarteten Häufigkeitsverteilung übereinstimmt. Nehmen wir zum Beispiel an, eine Gruppe von Patienten hat sich einer experimentellen Behandlung unterzogen und ihr Gesundheitszustand wurde untersucht, um festzustellen, ob sich ihr Zustand verbessert hat, gleich geblieben ist oder sich verschlechtert hat. Mit einem Anpassungstest ließe sich feststellen, ob die Zahlen in den einzelnen Kategorien – Verbesserung, keine Veränderung, Verschlechterung – mit den Zahlen übereinstimmen, die bei der Standardbehandlung zu erwarten wären. Lassen Sie uns das Ganze mit etwas Psychologie weiterdenken.

Die Kartendaten

Im Laufe der Jahre haben viele Studien gezeigt, dass es Menschen schwerfällt, den Zufall zu simulieren. So sehr wir auch versuchen, nach dem Zufallsprinzip zu handeln, wir denken in Mustern und Strukturen. Wenn man uns bittet, „etwas nach dem Zufallsprinzip zu tun“, ist das, was Menschen tatsächlich tun, alles andere als zufällig. Die Untersuchung der menschlichen Zufälligkeit (oder Nicht-Zufälligkeit, je nachdem) wirft daher viele tiefgreifende psychologische Fragen darüber auf, wie wir über die Welt denken. Betrachten wir in diesem Zusammenhang eine sehr einfache Studie. Nehmen wir an, ich würde die Teilnehmer bitten, sich ein gemischtes Kartenspiel vorzustellen und in Gedanken eine Karte aus diesem imaginären Kartenspiel „zufällig“ auszuwählen. Nachdem sie sich für eine Karte entschieden haben, bitte ich sie, gedanklich eine zweite Karte auszuwählen. Bei beiden Karten wird die Farbe (Herz, Kreuz, Pik oder Karo) betrachtet, die die Teilnehmer gewählt haben. Nachdem ich, sagen wir, N =200 Personen gebeten habe, dies zu tun, möchte ich mir die Daten ansehen und herausfinden, ob die Karten, die die Leute wählten, wirklich zufällig waren oder nicht. Die Daten sind im Datensatz randomness enthalten, in dem man, wenn man ihn in jamovi öffnet und sich die Tabellenansicht ansieht, drei Variablen sieht. Diese sind eine id Variable, die jedem Teilnehmer einen eindeutigen Identifikator zuweist, und die beiden Variablen choice_1 und choice_2, welche die von den Teilnehmern gewählten Kartenfarben angeben.

Im Moment konzentrieren wir uns nur auf die erste Wahl, welche die Leute getroffen haben. Wir verwenden die Option Frequency tables unter Exploration → Descriptives, um zu zählen, wie oft wir beobachtet haben, dass die Leute eine bestimmte Farbe gewählt haben. Dies ist das Ergebnis:

clubs diamonds   hearts   spades
   35       51       64       50

Diese kleine Häufigkeitstabelle ist recht hilfreich. Wenn man sie sich ansieht, gibt es einen kleinen Hinweis darauf, dass die Leute eher Herz als Kreuz wählen, aber es ist nicht ganz klar, ob das wirklich stimmt oder ob es nur Zufall ist. Um das herauszufinden, müssen wir wahrscheinlich eine Art statistische Analyse durchführen, worüber ich im nächsten Abschnitt sprechen werde.

Von nun an werden wir diese Tabelle als die Daten betrachten, die wir analysieren wollen. Da ich jedoch (leider!) über diese Daten in mathematischen Begriffen sprechen muss, ist es vielleicht eine gute Idee, sich über die Notation im Klaren zu sein. In der mathematischen Notation verkürzen wir das für Menschen lesbare Wort „beobachtet“ auf den Buchstaben O (observed), und wir verwenden tiefgestellte Indizes, um die Position der Beobachtung zu kennzeichnen. So wird die zweite Beobachtung in unserer Tabelle in mathematischer Schreibweise als O₂ geschrieben. Die Beziehung zwischen den englischen Bezeichnungen und den mathematischen Symbolen wird im Folgenden dargestellt:

Bezeichnung	Index, i	mathematisches Symbol	Wert
Kreuz (♣)	1	O1	35
Karo (♢)	2	O2	51
hearts (♡)	3	O3	64
spades (♠)	4	O4	50

Ich hoffe, das ist ziemlich klar. Es ist auch erwähnenswert, dass Mathematiker lieber über allgemeine als über spezifische Dinge sprechen, daher werden Sie auch die Notation O_isehen, die sich auf die Anzahl der Beobachtungen bezieht, die in die i-te Kategorie fallen (wobei i 1, 2, 3 oder 4 sein kann). Wenn wir uns schließlich auf die Menge aller beobachteten Häufigkeiten beziehen wollen, fassen Statistiker alle beobachteten Werte in einem Vektor zusammen,[1] den ich als O bezeichnen werde.

O = (O₁, O₂, O₃, O₄)

Auch das ist nichts Neues oder Interessantes. Es ist nur eine Notation. Wenn ich sage, dass O = (35, 51, 64, 50) ist, ist alles, was ich tue, die Tabelle der beobachteten Häufigkeiten (d.h., observed) in mathematischer Notation zu beschreiben.

Nullhypothese und Alternativhypothese

Wie im letzten Abschnitt angedeutet, lautet unsere Forschungshypothese, dass „die Menschen die Karten nicht zufällig auswählen“. Wir wollen dies nun in einige statistische Hypothesen umwandeln und dann einen statistischen Test für diese Hypothesen konstruieren. Der Test, den ich Ihnen beschreiben werde, ist Pearson’s χ² (Chi-Quadrat) χ²-Anpassungstest (goodness-of-fit test). Wie so oft müssen wir mit der sorgfältigen Konstruktion unserer Nullhypothese beginnen. In diesem Fall ist das ziemlich einfach. Lassen Sie uns zunächst die Nullhypothese in Worten formulieren:

H₀: Alle vier Farben werden mit gleicher Wahrscheinlichkeit gewählt

Da es sich hier um Statistik handelt, müssen wir in der Lage sein, das Gleiche auf mathematische Weise zu sagen. Zu diesem Zweck verwenden wir die Schreibweise P_jfür die wahre Wahrscheinlichkeit, dass die j-te Farbe gewählt wird. Wenn die Nullhypothese wahr ist, dann hat jede der vier Farben eine Wahrscheinlichkeit von 25 %, ausgewählt zu werden. Mit anderen Worten: Unsere Nullhypothese besagt, dass P₁ = 0,25, P₂ = 0,25, P₃ = 0,25 und schließlich, dass P₄ = 0,25. So wie wir unsere beobachteten Häufigkeiten in einem Vektor O gruppieren können, der den gesamten Datensatz zusammenfasst, können wir P verwenden, um uns auf die Wahrscheinlichkeiten zu beziehen, die unserer Nullhypothese entsprechen. Wenn ich also den mit dem Vektor P = (P₁, P₂, P₃, P₄) die Wahrscheinlichkeiten für unsere Nullhypothese beschreibe, dann erhalten wir:

H₀: P = (0.25, 0.25, 0.25, 0.25)

In diesem speziellen Fall entspricht unsere Nullhypothese einem Vektor von Wahrscheinlichkeiten P, bei dem alle Wahrscheinlichkeiten gleich sind. Aber das muss nicht der Fall sein. Wenn die Versuchspersonen sich zum Beispiel vorstellen sollten, dass sie aus einem Kartenspiel ziehen, das doppelt so viele Kreuz-Karten enthält wie jede andere Farbe, dann würde die Nullhypothese etwa P = (0,4, 0,2, 0,2, 0,2) entsprechen. Solange die Wahrscheinlichkeiten alle positive Zahlen sind und die Summe 1 ergibt, ist dies eine völlig legitime Wahl für die Nullhypothese. Die häufigste Anwendung des Anpassungsgütetests ist jedoch der Test auf die Nullhypothese, dass alle Kategorien gleich wahrscheinlich sind, weshalb wir uns für unser Beispiel daran halten.

Was ist mit unserer Alternativhypothese, H₁? Uns geht es eigentlich nur darum, zu zeigen, dass die Wahrscheinlichkeiten nicht identisch sind (d. h. dass die Entscheidungen der Menschen nicht völlig zufällig waren). Folglich sehen die „menschenfreundlichen“ Versionen unserer Hypothesen wie folgt aus:

H₀: Alle vier Farben werden mit gleicher Wahrscheinlichkeit gewählt

H₁: Mindestens eine der Wahrscheinlichkeiten bei der Wahl der Spielfarbe beträgt nicht 0,25

und die „mathematische“ Version ist:

H₀: P = (0.25, 0.25, 0.25, 0.25)

H₁: P ≠ (0.25, 0.25, 0.25, 0.25)

Die „Anpassungsgüte“-Teststatistik

Zu diesem Zeitpunkt haben wir unsere beobachteten Häufigkeiten O und eine Sammlung von Wahrscheinlichkeiten P entsprechend der Nullhypothese, die wir testen wollen. Wir wollen nun einen Test der Nullhypothese konstruieren. Wie immer, wenn wir H₀ gegen H₁ testen wollen, benötigen wir eine Teststatistik. Der grundlegende Trick, den ein Anpassungsgütetest verwendet, besteht darin, eine Teststatistik zu konstruieren, die misst, wie „nah“ die Daten an der Nullhypothese sind. Wenn die Daten nicht dem ähneln, was man „erwarten“ würde, wenn die Nullhypothese wahr wäre, dann ist sie wahrscheinlich nicht wahr. Wenn die Nullhypothese wahr wäre, was würden wir dann erwarten zu sehen? Oder, um die korrekte Terminologie zu verwenden, was sind die erwarteten Häufigkeiten. Es gibt N = 200 Beobachtungen, und (wenn die Nullhypothese wahr ist) ist die Wahrscheinlichkeit, dass eine von ihnen ein Herz auswählt, P₃ = 0,25, also schätze ich, wir erwarten 200 · 0,25 = 50 Herzen, richtig? Oder, genauer gesagt, wenn wir E_i auf „die Anzahl der Antworten der Kategorie i, die wir erwarten, wenn die Nullhypothese wahr ist“ beziehen, dann:

E_i = N · P_i

Wenn es 200 Beobachtungen gibt, die in vier Kategorien fallen können, und wir denken, dass alle vier Kategorien gleich wahrscheinlich sind, dann würden wir im Durchschnitt 50 Beobachtungen in jeder Kategorie erwarten, oder?

Wie lässt sich dies nun in eine Teststatistik übersetzen? Wir wollen natürlich die erwartete Anzahl der Beobachtungen in jeder Kategorie (E_i) mit der beobachteten Anzahl der Beobachtungen in dieser Kategorie (O_i) vergleichen. Und auf der Grundlage dieses Vergleichs sollten wir in der Lage sein, eine gute Teststatistik zu erstellen. Berechnen wir zunächst die Differenz zwischen dem, was die Nullhypothese erwarten ließ, und dem, was wir tatsächlich gefunden haben. Das heißt, wir berechnen den „beobachteten minus erwarteten“ Differenzwert, O_i - E_i. Dies wird in der folgenden Tabelle veranschaulicht:

		♣	♢	♡	♠
Erwartete Häufigkeit	Ei	50	50	50	50
Beobachtete Häufigkeit	O1	35	51	64	50
Differenzwert	Ei - O1	-15	1	14	0

Nach unseren Berechnungen ist es also klar, dass die Leute mehr Herz und weniger Kreuz gewählt haben, als die Nullhypothese vorhersagt. Ein kurzer Moment des Nachdenkens legt jedoch nahe, dass diese rohen Unterschiede nicht ganz das sind, wonach wir suchen. Intuitiv scheint es genauso schlimm zu sein, wenn die Nullhypothese zu wenige Beobachtungen vorhersagt (was bei Herz der Fall war), wie wenn sie zu viele vorhersagt (was bei Kreuz der Fall war). Es ist also etwas seltsam, dass wir eine negative Zahl für Kreuz und eine positive Zahl für Herz haben. Eine einfache Möglichkeit, dies zu beheben, besteht darin, alles zu quadrieren, so dass wir jetzt die quadrierten Differenzen berechnen, (O_i - O_i)². Wie zuvor können wir dies von Hand tun:

(observed - expected) ^ 2
   clubs diamonds   hearts   spades
     225        1      196        0

Jetzt machen wir Fortschritte. Was wir jetzt haben, ist eine Sammlung von Zahlen, die groß sind, wenn die Nullhypothese eine schlechte Vorhersage macht (Kreuz und Herz), aber klein, wenn sie eine gute Vorhersage macht (Karo und Pik). Aus technischen Gründen, die ich gleich erläutern werde, teilen wir nun alle diese Zahlen durch die erwartete Häufigkeit E_i, so dass wir eigentlich \(\frac{(E_i-O_i)^2}{E_i}\)berechnen. Da E_i = 50 für alle Kategorien in unserem Beispiel, ist es keine sehr interessante Berechnung, aber lassen Sie es uns trotzdem tun:

(observed - expected) ^ 2 / expected
   clubs diamonds   hearts   spades
    4.50     0.02     3.92     0.00

Wir haben es hier mit vier verschiedenen „Fehler“-Werten zu tun, von denen jeder angibt, wie groß der „Fehler“ der Nullhypothese war, als wir versuchten, mit ihr unsere beobachteten Häufigkeiten vorherzusagen. Um dies in eine nützliche Teststatistik umzuwandeln, könnten wir diese Zahlen einfach addieren. Das Ergebnis wird als Anpassungsgüte bezeichnet, die üblicherweise entweder als χ² (Chi-Quadrat) oder GOF (goodness-of-fit) bezeichnet wird. Wir können es wie folgt berechnen:

sum((observed - expected) ^ 2 / expected)

Dies ergibt einen Wert von 8,44.

Wenn wir k auf die Anzahl der Kategorien beziehen (d. h. k = 4 für unsere Kartendaten), dann ist die χ²-Statistik gegeben durch:

\[\chi^2 = \sum_{i=1}^k \frac{(O_i - E_i)^2}{E_i}\]

Intuitiv ist klar, dass, wenn χ² klein ist, die beobachteten Daten O_i sehr nahe an dem liegen, was die Nullhypothese vorhersagt E_i, so dass wir eine große χ²-Statistik benötigen, um die Nullhypothese zurückzuweisen.

Wie wir anhand unserer Berechnungen gesehen haben, ergibt sich für unseren Kartendatensatz ein Wert von χ² = 8,44. Nun stellt sich die Frage, ob dieser Wert groß genug ist, um die Null zu verwerfen?

Die Stichprobenverteilung der GOF-Statistik

Um festzustellen, ob ein bestimmter Wert von χ² groß genug ist, um eine Ablehnung der Nullhypothese zu rechtfertigen, müssen wir herausfinden, wie die Stichprobenverteilung für χ² aussehen würde, wenn die Nullhypothese wahr wäre. Das ist es, was ich in diesem Abschnitt tun werde. Ich zeige Ihnen in aller Ausführlichkeit, wie diese Stichprobenverteilung aufgebaut ist, und verwende sie dann im nächsten Abschnitt, um einen Hypothesentest zu erstellen. Wenn Sie es auf den Punkt bringen wollen und bereit sind, darauf zu vertrauen, dass die Stichprobenverteilung eine χ²-Verteilung mit k - 1 Freiheitsgraden ist, können Sie den Rest dieses Abschnitts auslassen. Wenn Sie jedoch verstehen wollen, warum der Anpassungsgütetest so funktioniert, wie er funktioniert, lesen Sie einfach weiter.

Nehmen wir an, dass die Nullhypothese tatsächlich wahr ist. Wenn ja, dann ist die wahre Wahrscheinlichkeit, dass eine Beobachtung in die i-te Kategorie fällt, P_i. Das ist ja so ziemlich die Definition unserer Nullhypothese. Lassen Sie uns darüber nachdenken, was das eigentlich bedeutet. Das ist in etwa so, als würde „die Natur“ die Entscheidung darüber treffen, ob die Beobachtung in der Kategorie i landet oder nicht, indem sie eine gewichtete Münze wirft (d. h. eine, bei der die Wahrscheinlichkeit, Kopf zu bekommen, P_j). Und deshalb können wir uns unsere beobachtete Häufigkeit O_i vorstellen, indem wir uns vorstellen, dass die Natur N dieser Münzen geworfen hat (eine für jede Beobachtung im Datensatz) und genau O_i davon Kopf ergab. Das ist natürlich eine ziemlich seltsame Art, über das Experiment nachzudenken. Aber es erinnert Sie (hoffentlich) daran, dass wir dieses Szenario schon einmal gesehen haben. Es ist genau derselbe Aufbau, der zur Binomialverteilung geführt hat. Mit anderen Worten: Wenn die Nullhypothese wahr ist, dann folgt daraus, dass unsere beobachteten Häufigkeiten durch Stichproben aus einer Binomialverteilung erzeugt wurden:

O_i ~ Binomial(P_i, N)

Wenn Sie sich an die Diskussion über den zentralen Grenzwertsatz erinnern, nähert sich das Aussehen der Binomialverteilung der Normalverteilung an, insbesondere wenn N groß ist und wenn P_i nicht zu nah an 0 oder 1 ist. Mit anderen Worten: Solange *N · P_i groß genug ist. Oder anders ausgedrückt: Wenn die erwartete Häufigkeit E_i groß genug ist, dann entspricht die theoretische Verteilung von O_i ungefähr der Normalverteilung. Besser noch: Wenn O_i normalverteilt ist, dann ist es auch \((O_i - E_i)/\sqrt{E_i}\). Da E_i ein fester Wert ist, werden durch Subtraktion von E_i und Division durch \(\sqrt{E_i}\) der Mittelwert und die Standardabweichung der Normalverteilung verändert, aber das ist auch schon alles. Schauen wir uns nun an, was unsere Anpassungsgüte-Statistik eigentlich ist: Was wir tun, ist, eine Reihe von normalverteilten Werten zu nehmen, sie zu quadrieren und sie zu addieren. Moment mal! Das haben wir auch schon mal gesehen! Wie wir in Weitere nützliche Verteilungen besprochen haben, hat die resultierende Menge eine χ²-Verteilung, wenn man eine Menge von Dingen nimmt, die eine Standardnormalverteilung haben (d.h. Mittelwert 0 und Standardabweichung 1), sie quadriert und dann addiert. Jetzt wissen wir also, dass die Nullhypothese vorhersagt, dass die Stichprobenverteilung der Anpassungsgüte-Statistik eine χ²-Verteilung ist.

Es gibt noch ein letztes Detail zu besprechen, nämlich die Freiheitsgrade. Wenn Sie sich an Weitere nützliche Verteilungen erinnern, habe ich gesagt, dass, wenn die Anzahl der Dinge, die Sie addieren, k ist, dann sind die Freiheitsgrade für die resultierende χ²-Verteilung k. Ich habe jedoch zu Beginn dieses Abschnitts gesagt, dass die tatsächlichen Freiheitsgrade für den χ²-Anpassungstest (goodness-of-fit test) k - 1 sind. Was ist damit? Die Antwort ist, dass wir eigentlich die Anzahl der wirklich unabhängigen Dinge betrachten sollten, die zusammenaddiert werden. Und wie ich im nächsten Abschnitt erläutern werde, sind trotz der k Dinge, die wir addieren, nur k - 1 davon wirklich unabhängig, so dass die Freiheitsgrade tatsächlich nur k - 1 sind. Das ist das Thema des nächsten Abschnitts.[2]

Freiheitsgrade

Als ich die χ²-Verteilung in Weitere nützliche Verteilungen vorgestellt habe, war ich etwas vage, was „Freiheitsgrade“ eigentlich bedeutet. Offensichtlich ist es von Bedeutung. Ein Blick auf Abb. 75 zeigt, dass sich die Form der χ²-Verteilung ganz erheblich ändert, wenn wir die Anzahl der Freiheitsgrade ändern. Aber was genau bedeutet das? Auch hier habe ich bei der Einführung der Verteilung und der Erklärung ihrer Beziehung zur Normalverteilung eine Antwort gegeben: Es ist die Anzahl der „normalverteilten Variablen“, die ich quadriere und addiere. Aber für die meisten Menschen ist das ziemlich abstrakt und nicht sehr hilfreich. Was wir wirklich tun müssen, ist zu versuchen, die Freiheitsgrade in Bezug auf unsere Daten zu verstehen.

Abb. 75 χ² (Chi-Quadrat)-Verteilungen mit einer unterschiedlichen Anzahl von „Freiheitsgraden“

Die Grundidee der Freiheitsgrade ist recht einfach. Man berechnet sie, indem man die Anzahl der verschiedenen „Größen“ zählt, die zur Beschreibung der Daten verwendet werden, und dann alle „Einschränkungen“ abzieht, die diese Daten erfüllen müssen.[3] Das ist etwas vage, also lassen Sie uns unsere Kartendaten als konkretes Beispiel verwenden. Wir beschreiben unsere Daten mit vier Zahlen, O₁, O₂, O₃ und O₄, die den beobachteten Häufigkeiten der vier verschiedenen Kategorien (Herz, Kreuz, Karo, Pik) entsprechen. Diese vier Zahlen sind die Zufallsresultate unseres Experiments. Aber mein Experiment hat eine feste Einschränkung: die Stichprobengröße N.[4] Das heißt, wenn wir wissen, wie viele Leute Herz, Karo und Kreuz gewählt haben, dann können wir genau herausfinden, wie viele Pik gewählt haben. Mit anderen Worten: Obwohl unsere Daten mit vier Zahlen beschrieben werden, entsprechen sie eigentlich nur 4 - 1 = 3 Freiheitsgraden. Eine etwas andere Sichtweise ist die, dass es vier Wahrscheinlichkeiten gibt, an denen wir interessiert sind (die wiederum den vier verschiedenen Kategorien entsprechen). Diese Wahrscheinlichkeiten müssen sich aber zu eins summieren, was eine Einschränkung bedeutet. Daher beträgt der Freiheitsgrad 4 - 1 = 3. Unabhängig davon, ob man es in Bezug auf die beobachteten Häufigkeiten oder in Bezug auf die Wahrscheinlichkeiten betrachten möchte, ist die Antwort dieselbe. Wenn man den χ² (Chi-Quadrat)-Anpassungstest für ein Experiment mit k Gruppen durchführt, dann sind die Freiheitsgrade im Allgemeinen k - 1.

Prüfen der Nullhypothese

Der letzte Schritt bei der Konstruktion unseres Hypothesentests besteht darin, den Ablehnungsbereich zu bestimmen. Das heißt, welche Werte von χ² würden dazu führen, dass wir die Nullhypothese ablehnen. Wie wir bereits gesehen haben, bedeuten große Werte von χ², dass die Nullhypothese die Daten unseres Experiments schlecht vorhersagt. Dagegen bedeuten kleine Werte von χ², dass die Nullhypothese recht gut funktioniert. Daher ist es eine vernünftige Strategie, zu sagen, dass es einen kritischen Wert gibt, wobei wir die Nullhypothese verwerfen, wenn χ² größer als der kritische Wert ist. Ist χ² kleiner als dieser Wert, behalten wir die Nullhypothese bei. Mit anderen Worten, um die Sprache zu verwenden, die wir in Kapitel Das Überprüfen von Hypothesen eingeführt haben, ist der χ²-Anpassungstest (χ²-Goodness of Fit-Test) immer ein einseitiger Test. Wir müssen also nur noch herausfinden, wie hoch der kritische Wert ist. Und das ist ziemlich einfach. Wenn unser Test ein Signifikanzniveau von α = 0,05 haben soll (d. h. wir sind bereit, eine Typ-I-Fehlerrate von 5 % zu tolerieren), dann müssen wir unseren kritischen Wert so wählen, dass die Wahrscheinlichkeit dafür, dass die Nullhypothese wahr ist, wenn χ² so groß wird, nur 5 % beträgt. Dies wird in Abb. 76 veranschaulicht.

Abb. 76 Veranschaulichung der Vorgehensweise beim Hypothesentesten für den χ² (Chi-Quadrat)-Anpassungstest

Aber wie findet man den kritischen Wert einer χ²-Verteilung mit k - 1 Freiheitsgraden? Vor vielen, vielen Jahren, als ich zum ersten Mal einen Statistikkurs in Psychologie belegte, haben wir diese kritischen Werte in einem Buch mit kritischen Wertetabellen nachgeschlagen, wie die in Tab. 11. Wir können sehen, dass der kritische Wert für eine χ²-Verteilung mit 3 Freiheitsgraden und p = 0,05 7,815 beträgt.

Tab. 11 Tabelle mit den kritischen Werten für die χ²-Verteilung (Chi-Quadrat)

df	Wahrscheinlichkeit
	nicht signifikant						signifikant
	0.95	0.90	0.70	0.50	0.30	0.10	0.05	0.01	0.001
1	0.004	0.016	0.148	0.455	1.074	2.706	3.841	6.635	10.828
2	0.103	0.211	0.713	1.386	2.408	4.605	5.991	9.210	13.816
3	0.352	0.584	1.424	2.366	3.665	6.251	7.815	11.345	16.266
4	0.711	1.064	2.195	3.357	4.878	7.779	9.488	13.277	18.467
5	1.145	1.610	3.000	4.351	6.064	9.236	11.070	15.086	20.515
6	1.635	2.204	3.828	5.348	7.231	10.645	12.592	16.812	22.458
7	2.167	2.833	4.671	6.346	8.383	12.017	14.067	18.475	24.322
8	2.733	3.490	5.527	7.344	9.524	13.362	15.507	20.090	26.124
9	3.325	4.168	6.393	8.343	10.656	14.684	16.919	21.666	27.877
10	3.940	4.865	7.267	9.342	11.781	15.987	18.307	23.209	29.588

Wenn also unsere berechnete χ²-Statistik größer ist als der kritische Wert von 7,815, dann können wir die Nullhypothese verwerfen (zur Erinnerung: die Nullhypothese, H₀, besagt, dass alle vier Farben mit gleicher Wahrscheinlichkeit gewählt werden). Da wir das bereits berechnet haben (d.h. χ² = 8,44), können wir die Nullhypothese verwerfen. Und das war’s im Grunde. Sie kennen jetzt den „Pearson’s χ²-Anpassungstest“.

Durchführen des Tests in jamovi

Es überrascht wahrscheinlich nicht, dass jamovi eine Analyse anbietet, die diese Berechnungen für Sie durchführt. Wählen Sie Frequencies (unter Analyses) → One Sample Proportion Tests → N Outcomes. Verschieben Sie dann in den erscheinenden Eingabeoptionen die Variable, die Sie analysieren möchten (choice_1) in das Feld Variable. Klicken Sie außerdem auf die Checkbox Expected counts , um die erwarteten Werte in der Ergebnistabelle anzuzeigen. Wenn Sie das getan haben, sollten Sie die Analyseergebnisse in jamovi ähnlich denen in Abb. 77 sehen. Es ist keine Überraschung, dass jamovi die gleichen erwarteten Werte und die gleichen Statistiken liefert, die wir zuvor von Hand berechnet haben: einen χ²-Wert von 8,44 mit df = 3 und p =0,038. Beachten Sie, dass wir nicht mehr nach einem kritischen p-Schwellenwert suchen müssen, da jamovi uns den tatsächlichen p-Wert des berechneten χ² für df = 3 liefert.

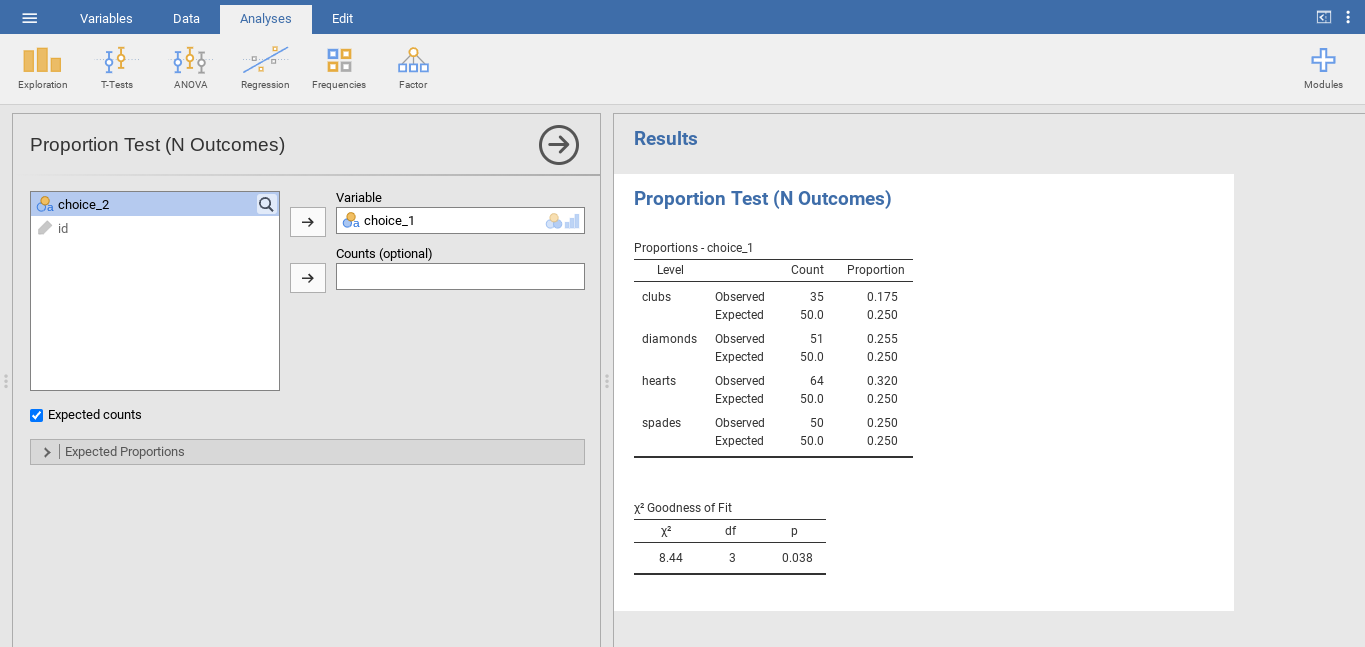
Abb. 77 χ²-Anpassungstest in jamovi, mit einer Tabelle, die sowohl die beobachteten als auch die erwarteten Häufigkeiten und Proportionen zeigt

Festlegen einer anderen Nullhypothese

An dieser Stelle fragen Sie sich vielleicht, was zu tun ist, wenn Sie einen χ²-Anpassungstest (χ² Goodness of Fit-Test) durchführen wollen, Ihre Nullhypothese aber nicht lautet, dass alle Kategorien gleich wahrscheinlich sind. Nehmen wir zum Beispiel an, dass jemand die theoretische Vorhersage getroffen hat, dass die Menschen in 60 % der Fälle rote Karten und in 40 % der Fälle schwarze Karten wählen sollten (ich habe keine Ahnung, warum man das vorhersagen sollte), aber keine anderen Präferenzen hat. In diesem Fall wäre die Nullhypothese, dass 30 % der Entscheidungen auf Herz, 30 % auf Karo, 20 % auf Pik und 20 % auf Kreuz fallen. Mit anderen Worten: Wir würden erwarten, dass Herz und Karo 1,5 Mal häufiger vorkommen als Pik und Kreuz (das Verhältnis 30 % : 20 % ist dasselbe wie 1,5 : 1). Das scheint mir eine dumme Theorie zu sein, und es ist ziemlich einfach, diese explizit angegebene Nullhypothese mit den Daten in unserer jamovi-Analyse zu testen. Im Analysefenster (in Abb. 77 mit Proportion Test (N Outcomes) bezeichnet) können Sie die Optionen für Expected Proportions erweitern. In diesem Fall können Sie verschiedene Verhältniswerte für die von Ihnen ausgewählte Variable eingeben, in unserem Fall choice_1. Ändern Sie das Verhältnis, um die neue Nullhypothese widerzuspiegeln, wie in Abb. 78 gezeigt, und sehen Sie, wie sich die Ergebnisse verändern.

Die erwarteten Häufigkeiten sind jetzt:

		♣	♢	♡	♠
Erwartete Häufigkeit	Ei	40	60	60	40

und die χ²-Statistik ist 4,74, df = 3, p = 0,192. Jetzt sind die Ergebnisse unserer aktualisierten Hypothesen und die erwarteten Häufigkeiten anders als beim letzten Mal. Infolgedessen ist unsere χ²-Teststatistik anders, und unser p-Wert ist ebenfalls anders. Ärgerlicherweise ist der p-Wert nun 0,192, so dass wir die Nullhypothese nicht zurückweisen können (siehe Abschnitt Der p-Wert eines Tests, um sich daran zu erinnern, warum das so ist). Obwohl die Nullhypothese einer eher dummen Theorie entspricht, liefern diese Daten leider nicht genügend Belege gegen sie.

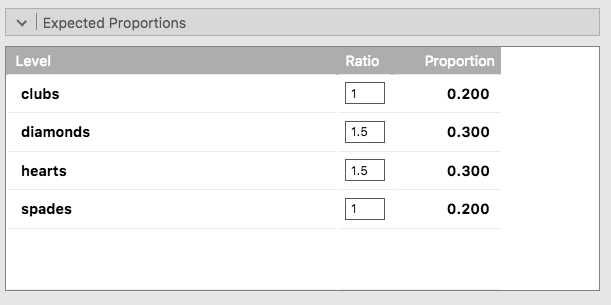
Abb. 78 Ändern der erwarteten Proportionen im χ²-Anpassungstest in jamovi

Wie berichten Sie diese Testergebnisse?

Jetzt wissen Sie also, wie der Test funktioniert und wie Sie ihn mit einem wunderbaren, nach jamovi duftenden magischen Rechenkasten durchführen können. Als Nächstes müssen Sie wissen, wie man die Ergebnisse aufschreibt. Schließlich macht es keinen Sinn, ein Experiment zu planen, durchzuführen und die Daten zu analysieren, wenn man niemandem davon erzählt! Lassen Sie uns nun darüber sprechen, was Sie bei der Berichterstattung über Ihre Analyse tun müssen. Bleiben wir bei unserem Beispiel mit den Spielkarten. Wenn ich dieses Ergebnis für eine Zeitschrift (oder ähnliches) aufschreiben wollte, dann wäre die konventionelle Art, darüber zu berichten, so etwas wie die folgenden Sätze:

Von den 200 Teilnehmern des Experiments entschieden sich 64 für Herz als erste Wahl, 51 für Karo, 50 für Pik und 35 für Kreuz. Ein χ²-Anpassungstest wurde durchgeführt, um zu prüfen, ob die Wahlwahrscheinlichkeiten für alle vier Spielfarben identisch waren. Die Ergebnisse waren signifikant (χ²(3) = 8,44, p < 0,05), was darauf hindeutet, dass die Personen die Spielfarben nicht rein zufällig gewählt haben.

Das ist ziemlich einfach und erscheint hoffentlich nicht besonders bemerkenswert. Dennoch gibt es ein paar Dinge, die Sie bei Ihrer Beschreibung beachten sollten:

• Dem statistischen Test geht die deskriptive Statistik voraus. Das heißt, ich habe dem Leser die Daten beschrieben, bevor ich den Hypothesentest durchführe. Im Allgemeinen ist dies eine gute Vorgehensweise. Denken Sie immer daran, dass Ihre Leser Ihre Daten nicht so gut kennt wie Sie selbst. Wenn Sie sie also nicht richtig beschreiben, werden die statistischen Tests für sie keinen Sinn ergeben und sie werden frustriert sein.

• Die Beschreibung gibt Auskunft über die zu prüfende Nullhypothese. Autoren tun dies leider nicht immer, aber es ist oft eine gute Idee; besonders in Situationen, in denen eine gewisse Mehrdeutigkeit besteht, oder wenn Sie sich nicht darauf verlassen können, dass Ihre Leserschaft mit den von Ihnen verwendeten statistischen Instrumenten vertraut ist. Oftmals kennt der Leser nicht alle Details des von Ihnen verwendeten Tests (oder kann sich nicht daran erinnern), so dass es eine Art von Höflichkeit ist, ihn daran zu „erinnern“! Was den χ²-Anpassungstest angeht, so kann man sich in der Regel darauf verlassen, dass das wissenschaftliche Publikum weiß, wie er funktioniert (da er in den meisten Statistik-Einführungskursen behandelt wird). Dennoch ist es eine gute Idee, die Nullhypothese (kurz!) explizit anzugeben, da die Nullhypothese je nachdem, wofür Sie den Test verwenden, unterschiedlich sein kann. Im Kartenbeispiel war meine Nullhypothese beispielsweise, dass die vier Wahrscheinlichkeiten für die die Spielfarben identisch sind (d. h. P₁ = P₂ = P₃ = P₄ = 0,25), aber diese Hypothese ist nichts Besonderes. Ich hätte genauso gut die Nullhypothese P₁ = 0,7 und P₂ = P₃ = P₄ = 0,1 mit einem χ²-Anpassungstest untersuchen können. Es ist also hilfreich für den Leser, wenn Sie ihm erklären, was Ihre Nullhypothese war. Beachten Sie auch, dass ich die Nullhypothese in Worten und nicht in Mathematik beschrieben habe. Es ist völlig in Ordnung, die Nullhypothese in mathematischer Form beschreiben, aber die meisten Leser können Worte leichter lesen als Symbole, und daher tendieren die meisten Autoren dazu, die Nullhypothese mit Worten zu beschreiben, wenn sie können.

• Der Bericht enthält einen „statistischen Block“. Beim Berichten der Testergebnisse selbst habe ich nicht nur gesagt, dass das Ergebnis signifikant war, sondern ich habe einen „Statistikblock“ hinzugefügt (d. h. den mathematisch aussehenden Teil mit mehreren Werten in den Klammern), der alle „wichtigen“ statistischen Informationen enthält. Für den χ²-Anpassungstest werden folgende Informationen angegeben: die Teststatistik (die χ²-Anpassungsgüte-Statistik betrug 8,44), die Informationen über die im Test verwendete Verteilung (χ² mit 3 Freiheitsgraden, was gewöhnlich mit χ²(3) abgekürzt wird) und die Information, ob das Ergebnis signifikant war (in diesem Fall p < 0,05). Die Informationen, die jeweils in den Statistikblock gehören, sind für jeden Test anders. Deshalb zeige ich Ihnen jedes Mal, wenn ich einen neuen Test vorstelle, wie der Statistikblock aussehen sollte.[5] Der allgemeine Grundsatz ist jedoch, dass Sie immer genügend Informationen berichten sollten, damit der Leser die Testergebnisse selbst überprüfen kann, wenn er dies wirklich möchte.

• Die Ergebnisse werden interpretiert. Ich habe nicht nur angegeben, dass das Ergebnis signifikant ist, sondern auch eine Interpretation des Ergebnisses geliefert (d. h., dass die Leute nicht zufällig gewählt haben). Dies ist auch eine Erleichterung für den Leser, denn es sagt ihm etwas darüber, was er über die Vorgänge in Ihren Daten glauben sollte. Wenn Sie so etwas nicht erwähnen, ist es für den Leser oft schwer zu verstehen, was vor sich geht.[6]

Ihr wichtigstes Anliegen sollte sein, Ihrem Leser Dinge zu erklären. Denken Sie immer daran, dass es beim Berichten Ihrer Ergebnisse darum geht, einem anderen Menschen etwas mitzuteilen. Ich kann Ihnen gar nicht sagen, wie oft ich den Ergebnisteil von Berichten, Dissertationen oder wissenschaftlichen Artikeln gesehen habe, der einfach nur Kauderwelsch ist, weil der Verfasser sich nur darauf konzentriert hat, alle Zahlen aufzuführen, und vergessen hat, mit dem menschlichen Leser zu kommunizieren.

Ein Kommentar zur statistischen Notation

Satan erfreut sich gleichermaßen an Statistiken und am Zitieren der Heiligen Schrift

– H.G. Wells

Wenn Sie sehr aufmerksam gelesen haben und genauso ein mathematischer Pedant sind wie ich, dann gibt es eine Schwäche an der Art und Weise, wie ich den χ²-Test im letzten Abschnitt geschrieben habe, die Sie vielleicht ein wenig stört. Es fühlt sich irgendwie falsch an, „χ²(3) = 8,44“ zu schreiben, werden Sie vielleicht denken. Immerhin ist es die Anpassungsgüte-Statistik, die gleich 8,44 ist, sollte ich also nicht χ² = 8,44 oder vielleicht GOF = 8,44 schreiben? Dabei wird scheinbar die Stichprobenverteilung (d.h., χ² mit df = 3) mit der Teststatistik (d.h., χ²) gleichgesetzt. Vielleicht dachten Sie, es handele sich um einen Tippfehler, da χ und X ziemlich ähnlich aussehen, aber das ist es nicht. Die Formulierung „χ²(3) = 8,44“ ist eine stark verkürzte Form der Formulierung „Die Stichprobenverteilung der Teststatistik ist χ²(3), und der Wert der Teststatistik ist 8,44“.

Das ist leider ziemlich dumm, weil es viele verschiedene Teststatistiken gibt, die eine χ²-Stichprobenverteilung aufweisen. Die χ²-Statistik, die wir für unseren Anpassungstest verwendet haben, ist nur eine von vielen (wenn auch eine der am häufigsten vorkommenden). In einer vernünftigen, perfekt organisierten Welt würden wir immer einen separaten Namen für die Teststatistik und die Stichprobenverteilung haben. Auf diese Weise würde der Statistikblock selbst Ihnen genau sagen, was der Forscher berechnet hat. Das kommt manchmal vor. Zum Beispiel wird die Teststatistik, die im χ²-Anpassungstest verwendet wird, χ² geschrieben, aber es gibt einen eng verwandten Test, der als G-Test bekannt ist (Sokal & Rohlf, 2011),[7] bei dem die Teststatistik als G geschrieben wird. Zufälligerweise testen der χ²-Anpassungstest und der G-Test beide die gleiche Nullhypothese, und die Stichprobenverteilung ist genau dieselbe (d.h., eine χ²-Verteilung mit k - 1 Freiheitsgraden). Hätte ich einen G-Test für die Kartendaten anstatt eines Anpassungsgütetests durchgeführt, dann hätte ich eine Teststatistik von G = 8,65 erhalten, die sich geringfügig von dem zuvor ermittelten Wert χ² = 8,44 unterscheidet und einen etwas kleineren p-Wert von p = 0,034 ergibt. Wenn die Konvention wäre, die Teststatistik, dann die Stichprobenverteilung und dann den p-Wert anzugeben, würden diese beiden Situationen zu unterschiedlichen Statistikblöcken führen: Mein ursprüngliches Ergebnis würde χ² = 8,44, χ²(3), p = 0,038 lauten, während die alternative Version mit dem G-Test G = 8,65, χ²(3), pÜ = 0,034 lauten würde. Bei Verwendung des verkürzten Berichtsstandards lautet das ursprüngliche Ergebnis jedoch χ²(3) = 8,44, *p = 0,038 und das neue Ergebnis χ²(3) = 8,65, p = 0,034, so dass es eigentlich unklar ist, welchen Test ich tatsächlich durchgeführt habe.

Warum leben wir also nicht in einer Welt, in welcher der Inhalt des Statistikblocks eindeutig angibt, welche Tests durchgeführt wurden? Der Hauptgrund ist, dass das Leben chaotisch ist. Wir (als Benutzer statistischer Werkzeuge) wollen, dass es schön, ordentlich und organisiert ist. Wir wollen, dass unser Bericht entworfen wird, als ob es ein Produkt wäre, aber so funktioniert das Leben nicht. Die Statistik ist eine intellektuelle Disziplin wie jede andere auch, und als solche ist sie ein stark verteiltes, teils kollaboratives und teils wettbewerbsorientiertes Projekt, das niemand wirklich vollständig versteht. Die Werkzeuge, die Sie und ich für die Datenanalyse verwenden, wurden nicht durch einen Akt der Götter der Statistik geschaffen. Sie wurden von vielen verschiedenen Leuten erfunden, in akademischen Fachzeitschriften veröffentlicht, von vielen anderen Leuten implementiert, korrigiert und verändert und dann von jemand anderem in Lehrbüchern erklärt. Infolgedessen gibt es eine Menge von Teststatistiken, die nicht einmal Namen haben. Infolgedessen werden sie einfach mit demselben Namen wie die entsprechende Stichprobenverteilung bezeichnet. Wie wir später sehen werden, wird jede Teststatistik, die einer χ²-Verteilung folgt, gemeinhin als „χ²-Statistik“ bezeichnet, alles, was einer t-Verteilung folgt, wird als „t-Statistik“ bezeichnet, und so weiter. Aber, wie das Beispiel χ² versus G zeigt, sind zwei verschiedene Dinge mit derselben Stichprobenverteilung immer noch verschieden.

Daher ist es gewöhnlich eine gute Idee, klar zu sagen, welchen Test Sie tatsächlich durchgeführt haben, insbesondere wenn Sie etwas Ungewöhnliches tun. Wenn Sie einfach „χ²-test“ sagen, ist nicht klar, welchen Test Sie eigentlich meinen. Da die beiden gebräuchlichsten χ²-Anpassungstest und der χ²-Unabhängigkeitstest sind, können die meisten Leser mit Statistikkenntnissen wahrscheinlich raten. Dennoch sollte man sich möglicher Fehlinterpretationen bewusst sein.

---

[1]

Ein Vektor ist eine Folge von Datenelementen desselben Grundtyps

[2]

Wenn man die Gleichung für die Anpassungsgüte-Statistik als eine Summe über k - 1 unabhängige Dinge umschreibt, erhält man die „richtige“ Stichprobenverteilung, nämlich die χ²-Verteilung mit k - 1 Freiheitsgraden. Es würde den Rahmen eines Einführungsbuchs sprengen, die mathematischen Zusammenhänge so detailliert darzustellen. Ich wollte Ihnen nur einen Eindruck davon vermitteln, wie die Anpassungsgüte-Statistik mit der χ²-Verteilung verbunden ist.

[3]

Ich fühle mich verpflichtet, darauf hinzuweisen, dass dies eine starke Vereinfachung ist! Sie funktioniert in vielen Situationen gut, aber hin und wieder werden wir auf Freiheitsgrade stoßen, die keine ganzen Zahlen sind. Lassen Sie sich davon nicht zu sehr beunruhigen; wenn Sie darauf stoßen, erinnern Sie sich einfach daran, dass „Freiheitsgrade“ in Wirklichkeit ein eher chaotisches Konzept sind. Daher ist die nette einfache Geschichte, die ich Ihnen hier erzähle, nicht die ganze Geschichte. Für einen Einführungskurs ist es normalerweise am besten, sich an die einfache Geschichte zu halten. Aber ich denke, es ist am besten, Sie zu warnen, dass diese einfache Geschichte nicht immer die komplexere Realität widerspiegelt. Wenn ich Sie nicht warnen würde, könnten Sie verwirrt werden, wenn Sie df = 3.4 oder so sehen, und (fälschlicherweise) denken, dass Sie etwas falsch verstanden haben. Stattdessen ist es so, dass die hier genutzte vereinfachte Darstellung nicht auf alle Analysesituationen passt.

[4]

In der Praxis ist die Stichprobengröße nicht immer festgelegt. Wir könnten das Experiment zum Beispiel über einen bestimmten Zeitraum durchführen, und die Anzahl der Teilnehmer hängt davon ab, wie viele Personen erscheinen. Für den aktuellen Zweck spielt das keine Rolle.

[5]

Zumindest teilweise. Die Konventionen für die Darstellung von Statistiken unterscheiden sich von Fachgebiet zu Fachgebiet etwas. Ich habe mich an den Gepflogenheiten in der Psychologie orientiert, da dies mein Fachgebiet ist. Aber der allgemeine Grundsatz, dem Leser genügend Informationen zur Verfügung zu stellen, damit er die Ergebnisse überprüfen kann, ist meiner Meinung nach ziemlich allgemein.

[6]

Für manche mag dieser Ratschlag seltsam klingen oder zumindest im Widerspruch zu den „üblichen“ Ratschlägen für das Verfassen eines Manuskripts (oder eines Berichts) stehen. In der Regel wird den Studenten gesagt, dass der Abschnitt „Ergebnisse“ eines Manuskripts der Beschreibung der Daten und der statistischen Analyse dient, während der Abschnitt „Diskussion“ der Interpretation dient. Das stimmt zwar im Großen und Ganzen, aber ich glaube, dass die Leute das oft viel zu wörtlich nehmen. Ich gehe in der Regel so vor, dass ich im Ergebnisteil eine schnelle und einfache Interpretation der Daten gebe, damit der Leser versteht, was die Daten aussagen. In der Diskussion versuche ich dann, eine umfassendere Übersicht darüber zu geben, ob und wie diese Ergebnisse mit der bisherigen wissenschaftlichen Literatur übereinstimmen. Kurz gesagt, lassen Sie nicht zu, dass der Ratschlag „Die Interpretation gehört in die Diskussion“ Ihren Ergebnisteil in unverständlichen Müll verwandelt. Vom Leser verstanden zu werden, ist viel wichtiger.

[7]

Erschwerend kommt hinzu, dass der G-Test ein Spezialfall einer ganzen Klasse von Tests ist, die als Likelihood-Ratio-Tests (LRT) bekannt sind. LRTs werden in diesem Buch nicht behandelt, aber es ist sehr nützlich, sie zu kennen.