Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft
Der t-Test bei einer Stichprobe
Nach einigem Nachdenken kam ich zu dem Schluss, dass wir nicht davon ausgehen können, dass die Noten der Psychologiestudenten die gleiche Standardabweichung haben wie die der anderen Studenten in Dr. Zeppos Klasse. Denn wenn ich die Hypothese vertrete, dass sie nicht den gleichen Mittelwert haben, warum sollte ich dann glauben, dass sie die gleiche Standardabweichung haben? In Anbetracht dessen sollte ich wirklich aufhören anzunehmen, dass ich den wahren Wert von σ kenne. Dies verstößt gegen die Annahmen meines z-Tests, so dass ich in gewisser Weise wieder am Anfang stehe. Es ist jedoch nicht so, dass ich völlig chancenlos bin. Schließlich habe ich immer noch meine Rohdaten, und diese Rohdaten erlauben eine Schätzung der Standardabweichung der Population, die 9,52 beträgt. Mit anderen Worten: Ich kann zwar nicht sagen, dass ich weiß, dass σ = 9,5 ist, aber ich kann sagen, dass \(\hat\sigma\) = 9,52 ist.
Das Naheliegendste, was Sie tun könnten, ist, einen z-Test durchzuführen, aber unter Verwendung der geschätzten Standardabweichung von 9,52, anstatt sich auf meine Annahme zu verlassen, dass die wahre Standardabweichung 9,5 ist. Und es würde Sie wahrscheinlich nicht überraschen zu hören, dass dies immer noch zu einem signifikanten Ergebnis führen würde. Dieser Ansatz ist nahe dran, aber er ist nicht ganz richtig. Da wir uns nun auf eine Schätzung der Standardabweichung in der Grundgesamtheit stützen, müssen wir eine gewisse Anpassung vornehmen, um der Tatsache Rechnung zu tragen, dass wir eine gewisse Unsicherheit darüber haben, wie hoch die tatsächliche Standardabweichung in der Grundgesamtheit ist. Vielleicht sind unsere Daten nur ein Glücksfall … vielleicht ist die wahre Standardabweichung in der Grundgesamtheit zum Beispiel 11. Aber wenn das tatsächlich der Fall wäre und wir den z-Test unter der Annahme von σ = 11 durchführen würden, dann wäre das Ergebnis nicht signifikant. Das ist ein Problem, das wir angehen müssen.
Abb. 85 Grafische Darstellung der Nullhypothese und der Alternativhypothese, die beim (zweiseitigen) t-Test mit einer Stichprobe angenommen werden. Man beachte die Ähnlichkeit mit dem z-Test Abb. 83. Die Nullhypothese lautet, dass der Mittelwert der Grundgesamtheit μ gleich einem bestimmten Wert μ0ist, und die Alternativhypothese lautet, dass er es nicht ist. Wie beim z-Test gehen wir davon aus, dass die Daten normalverteilt sind, aber wir nehmen nicht an, dass die Standardabweichung σ in der Grundgesamtheit im Voraus bekannt ist.
Einführung in den t-Test
Diese Zweideutigkeit ist ärgerlich und wurde 1908 von einem Mann namens William Sealy Gosset (Student, 1908) aufgelöst. Dieser arbeitete zu dieser Zeit als Chemiker für die Guinness-Brauerei (Box, 1987). Da Guinness es nicht gerne sah, wenn seine Mitarbeiter statistische Analysen veröffentlichten (offenbar hielten sie diese für ein Geschäftsgeheimnis), veröffentlichte er die Arbeit unter dem Pseudonym „A Student“, und bis heute lautet der vollständige Name des t-Tests eigentlich t-test nach Student. Das Wichtigste, was Gosset herausfand, ist die Frage, wie wir der Tatsache Rechnung tragen können, dass wir nicht ganz sicher sind, wie hoch die wahre Standardabweichung ist.[1] Die Antwort ist, dass sich die Stichprobenverteilung dadurch subtil ändert. Beim t-Test wird unsere Teststatistik, die jetzt t-Statistik genannt wird, auf genau dieselbe Weise berechnet, die ich oben erwähnt habe. Wenn unsere Nullhypothese lautet, dass der wahre Mittelwert µ ist, unsere Stichprobe aber den Mittelwert X̄ hat und unsere Schätzung der Standardabweichung der Grundgesamtheit \(\hat{\sigma}\) ist, dann lautet unsere t-Statistik:
Das Einzige, was sich in der Gleichung geändert hat, ist, dass wir an Stelle des bekannten wahren Wertes σ die Schätzung \(\hat{\sigma}\) verwenden. Und wenn diese Schätzung aus N Beobachtungen konstruiert wurde, dann wird die Stichprobenverteilung zu einer t-Verteilung mit N - 1 Freiheitsgraden (df). Die t-Verteilung ist der Normalverteilung sehr ähnlich, hat aber „schwerere“ Ausläufer, wie bereits in Weitere nützliche Verteilungen besprochen und in Abb. 86 dargestellt. Beachten Sie jedoch, dass die t-Verteilung mit zunehmender Größe von df beginnt, sich der Standard-Normalverteilung anzunähern. Das ist auch gut so: Bei einem Stichprobenumfang von N = 70.000.000 wäre Ihre „Schätzung“ der Standardabweichung ziemlich genau. Sie sollten also erwarten, dass sich der t-Test bei einem großen N genau so verhält wie ein z-Test. Und genau das passiert auch!
Abb. 86 Die t-Verteilung mit 2 Freiheitsgraden (links) und 10 Freiheitsgraden (rechts), mit einer Standard-Normalverteilung (d. h. Mittelwert = 0 und Standardabweichung = 1), die zu Vergleichszwecken als gepunktete Linien dargestellt ist. Beachten Sie, dass die t-Verteilung stärkere Ausläufer hat (leptokurtisch: höhere Kurtosis) als die Normalverteilung; dieser Effekt ist ziemlich übertrieben, wenn die Freiheitsgrade sehr klein sind, aber vernachlässigbar für größere Werte. Mit anderen Worten: Für große df ist die t-Verteilung im Wesentlichen identisch mit einer Normalverteilung.
Durchführen des Tests in jamovi
Wie zu erwarten, ist die Vorgehensweise beim t-Test fast identisch mit der Vorgehensweise beim z-Test. Es macht also wenig Sinn, Ihnen zu zeigen, wie Sie die Berechnungen mit Befehlen Schritt-für-Schritt durchführen. Die Berechnungen sind fast identisch mit denen, die wir zuvor durchgeführt haben, außer dass wir die geschätzte Standardabweichung verwenden und unsere Hypothese mit der t-Verteilung statt mit der Normalverteilung testen. Anstatt die Berechnungen ein zweites Mal in mühsamer Kleinarbeit durchzugehen, zeige ich Ihnen jetzt, wie t-Tests tatsächlich durchgeführt werden. jamovi enthält eine spezielle Analyse für t-Tests, die sehr flexibel ist (sie kann viele verschiedene Arten von t-Tests durchführen). Es ist ziemlich einfach zu benutzen; alles, was Sie tun müssen, ist Analyses → T-Tests → One Sample T-Test auszuwählen, die Variable, an der Sie interessiert sind (X), in das Feld Variables zu verschieben, und den Mittelwert für die Nullhypothese (67.5) im Textfeld Hypothesis → Test value einzutragen. Das ist ganz einfach (siehe Abb. 87, das, neben anderen Dingen, zu denen wir gleich noch kommen werden, eine t-Statistik = 2.25 ergibt, mit 19 Freiheitsgraden und einem zugehörigen p-Wert von 0.036.
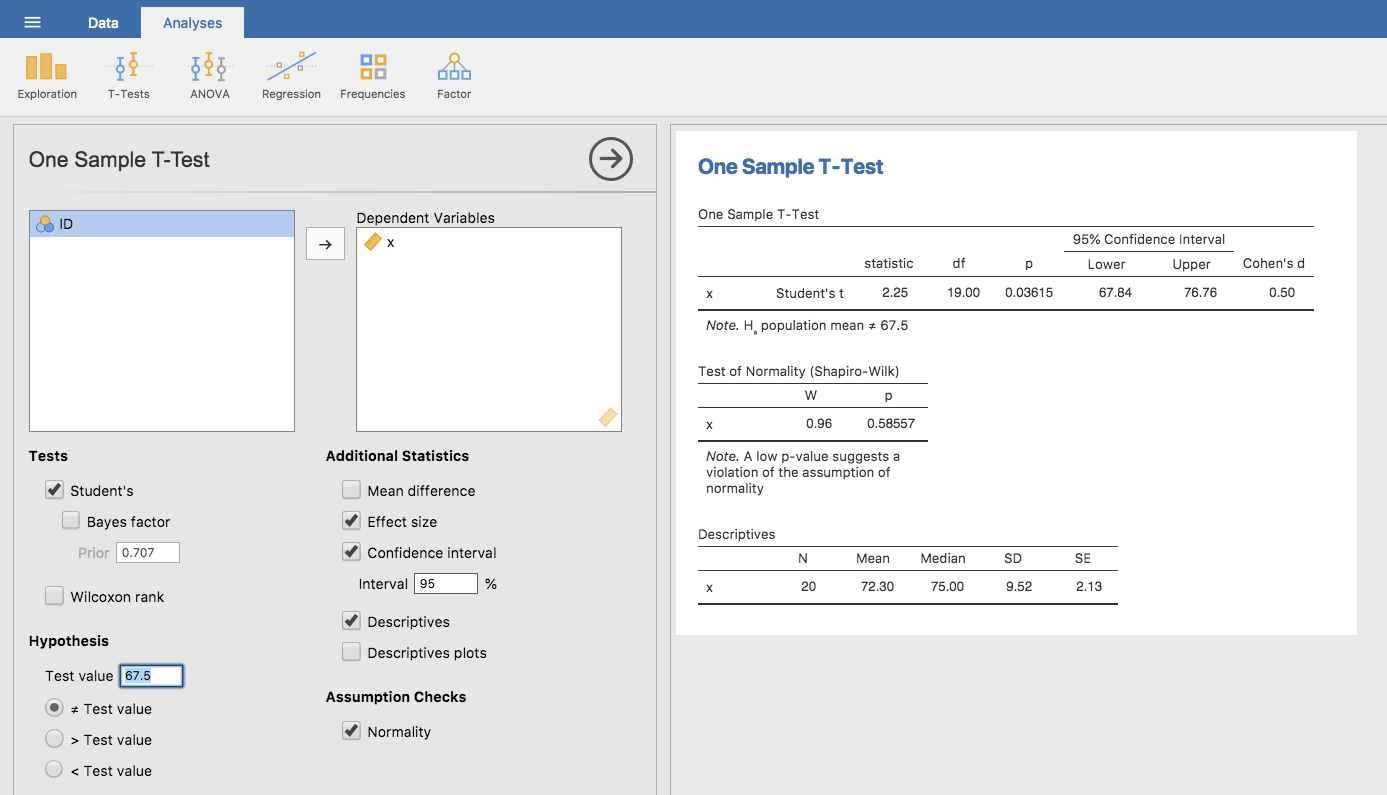
Abb. 87 Durchführen des t-Tests mit einer Stichprobe in jamovi
Es werden auch zwei andere Dinge berichtet, die für Sie von Interesse sein könnten: das 95%-Konfidenzintervall und ein Maß für die Effektstärke (wir werden später mehr über Effektstärken sprechen). Das scheint also einfach genug zu sein. Was machen wir nun mit dieser Ausgabe? Da wir so tun, als ob wir uns tatsächlich für mein Spielzeugbeispiel interessieren, sind wir überglücklich zu entdecken, dass das Ergebnis statistisch signifikant ist (d. h. einen p-Wert von unter 0,05 hat). Wir könnten das Ergebnis in etwa so wiedergeben:
Mit einer Durchschnittsnote von 72,3 lagen die Psychologiestudenten leicht über der Durchschnittsnote von 67,5 (t(19) = 2,25, p < 0,05); die mittlere Differenz betrug 4,80 und das 95%-Konfidenzintervall lag zwischen 0,34 und 9,26.
wobei t(19) die Kurzschreibweise für eine t-Statistik mit 19 Freiheitsgraden ist. Allerdings kommt es häufig vor, dass das Konfidenzintervall nicht angegeben wird oder in einer viel komprimierteren Form, als ich es hier getan habe. Es ist zum Beispiel nicht ungewöhnlich, dass das Konfidenzintervall als Teil des Statistikblocks nach der Angabe der Mittelwertdifferenz angegeben wird:
Bei so viel Fachjargon in einer halben Zeile weiß man, dass es wirklich schlau sein muss.[2]
Voraussetzungen für den t-Test bei einer Stichprobe
Welche Voraussetzungen müssen erfüllt sein, um den t-Test mit einer Stichprobe durchführen zu können? Da der t-Test im Grunde ein z-Test ist, bei dem die Annahme, dass die Standardabweichung bekannt sein muss, entfällt, sollte es Sie nicht überraschen, dass er dieselben Voraussetzungen erfordert wie der z-Test, abzüglich der Annahme der bekannten Standardabweichung. Das bedeutet
Normalverteilung. Wir gehen immer noch davon aus, dass die Grundgesamtheit normalverteilt ist,[3] und wie bereits erwähnt, gibt es Standardwerkzeuge, mit denen Sie überprüfen können, ob diese Annahme erfüllt ist (Abschnitt Überprüfen der Normalverteilung in einer Stichprobe), und andere Tests, die Sie durchführen können, wenn diese Annahme verletzt wird (Abschnitt Prüfen nicht-normalverteilter Daten mit dem Wilcoxon-Test).
Unabhängigkeit. Auch hier müssen wir davon ausgehen, dass die Beobachtungen in unserer Stichprobe unabhängig voneinander erzeugt wurden. Siehe die frühere Diskussion beim z-Test für Einzelheiten (Abschnitt Annahmen des *z*-Tests).
Insgesamt sind diese beiden Annahmen nicht sehr unvernünftig, und daher wird der t-Test mit einer Stichprobe in der Praxis recht häufig zum Vergleich eines Stichprobenmittelwerts mit einem hypothetischen Populationsmittelwert verwendet.