Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft

Der t-Test für unabhängige Stichproben (nach Student)

Obwohl der t-Test mit einer Stichprobe durchaus seine Berechtigung hat, ist er nicht das typischste Beispiel für einen t-Test.[1] Viel häufiger kommt es vor, dass man zwei verschiedene Gruppen von Beobachtungen hat. In der Psychologie entspricht dies in der Regel zwei verschiedenen Gruppen von Teilnehmern, wobei jede Gruppe einer Bedingung in Ihrer Studie entspricht. Für jede Person in der Studie messen Sie eine Ergebnisvariable von Interesse, und die Forschungsfrage, die Sie stellen, lautet, ob die beiden Gruppen denselben Populationsmittelwert haben oder nicht. Für diese Situation ist der t-Test für unabhängige Stichproben konzipiert.

Die Daten

Angenommen, 33 Studenten besuchen die Statistikvorlesungen von Dr. Harpo, und Dr. Harpo benotet nicht im Einklang mit einer Normalverteilungskurve. Stattdessen ist Dr. Harpos Benotung ein gewisses Mysterium. Wir wissen also nicht wirklich, wie die Durchschnittsnote für die gesamte Klasse lautet. Es gibt zwei Tutoren in dieser Klasse, Anastasia und Bernadette. Es gibt N₁ = 15 Schüler in Anastasias Tutorien und N₂ = 18 in Bernadettes Tutorien. Die Forschungsfrage, die mich interessiert, ist, ob Anastasia oder Bernadette die bessere Tutorin ist, oder ob es keinen großen Unterschied macht. Dr. Harpo schickt mir den Datensatz harpo mit den Kursnoten. Wie üblich lade ich die Datei in jamovi und schaue mir an, welche Variablen sie enthält - es gibt drei Variablen, ID, grade und tutor. Die Variable grade enthält die Note jedes Schülers, aber sie wird nicht mit dem richtigen Attribut für die Messungsebene in jamovi importiert, also muss ich dies ändern, damit sie als kontinuierliche Variable betrachtet wird (siehe Skalenniveau von Daten ändern). Die Variable tutor ist ein Faktor , der angibt, wer der Tutor des jeweiligen Schülers war: entweder Anastasia oder Bernadette.

Wir können Mittelwerte und Standardabweichungen berechnen, indem wir die Analyse Exploration → Descriptives verwenden. Wir erhalten dann die folgende zusammenfassende Tabelle:

	Mittelwert	Std.-abw.	N
Anastasias Studenten	74.53	9.00	15
Bernadettes Studenten	69.06	5.77	18

Um Ihnen einen detaillierteren Eindruck davon zu vermitteln, was hier vor sich geht, habe ich Histogramme (nicht in jamovi, sondern mit R) erstellt, welche die Verteilung der Noten für beide Tutoren (Abb. 88) zeigen, sowie eine einfachere Darstellung, welche die Mittelwerte und die entsprechenden Konfidenzintervalle für beide Schülergruppen (Abb. 89) zeigt.

Abb. 88 Histogramme, welche die Verteilung der Noten für Schüler in Anastasias (links) und Bernadettes (rechts) Tutorien zeigen. Die Histogramme deuten darauf hin, dass die Schüler in Anastasias Tutorien im Durchschnitt etwas bessere Noten erhalten, gleichzeitig scheinen die Noten aber auch etwas variabler zu sein.

Abb. 89 Die Diagramme zeigen die Durchschnittsnote der Schüler in den Tutorien von Anastasia und Bernadette. Die Fehlerbalken stellen die 95%-Konfidenzintervalle um den Mittelwert dar. Optisch sieht es so aus, als gäbe es einen reellen Unterschied zwischen den Gruppen, obwohl es schwer ist, das mit Sicherheit zu sagen.

Einführung in den Test

Den t-Test für unabhängige Stichproben gibt es in zwei verschiedenen Versionen, dem Test nach Student und dem von Welch. Der ursprüngliche t-Test nach Student, den ich in diesem Abschnitt beschreiben werde, ist der einfachere der beiden, beruht aber auf restriktiveren Annahmen als der t-Test von Welch. Angenommen, Sie möchten einen zweiseitigen Test durchführen, so besteht das Ziel darin, festzustellen, ob zwei „unabhängige Stichproben“ von Daten aus Populationen mit demselben Mittelwert (Nullhypothese) oder mit unterschiedlichen Mittelwerten (Alternativhypothese) gezogen wurden. Wenn wir von „unabhängigen“ Stichproben sprechen, meinen wir damit, dass es keine besondere Beziehung zwischen den Beobachtungen in den beiden Stichproben gibt. Das macht im Moment wahrscheinlich nicht viel Sinn, aber es wird klarer, wenn wir später über den t-Test für gepaarte Stichproben sprechen. Für den Moment wollen wir nur darauf hinweisen, dass wir einen t-Test für unabhängige Stichproben (und nicht einen t-Test für gepaarte Stichproben) benutzen sollten, wenn wir einen Versuchsplan haben, bei dem die Teilnehmer zufällig einer von zwei Gruppen zugewiesen werden, und wir die mittlere Leistung der beiden Gruppen bei einer Ergebnismessung vergleichen wollen.

Wir bezeichnen µ₁ als den wahren Populationsmittelwert für Gruppe 1 (z.B. Anastasias Studenten), und µ₂ als den wahren Populationsmittelwert für Gruppe 2 (z.B. Bernadette Studenten).[2] Wie üblich bezeichnen wir die beobachteten Stichprobenmittelwerte für diese beiden Gruppen mit X̄_{1`und *X̄*:sub:`2}. Unsere Nullhypothese besagt, dass die beiden Populationsmittelwerte identisch sind (µ₁ = µ₂), und die Alternativhypothese ist, dass sie es nicht sind (µ₁ ≠ µ₂). In mathematischer Sprache ausgedrückt bedeutet dies:

H₀: µ₁ = µ₂

H₁: µ₁ ≠ µ₂

Abb. 90 Grafische Veranschaulichung der Null- und Alternativhypothesen, die beim t-Test für unabhängige Stichproben (nach Student) angenommen werden. Die Nullhypothese geht davon aus, dass beide Gruppen den gleichen Mittelwert µ haben, während die Alternativhypothese davon ausgeht, dass sie unterschiedliche Mittelwerte µ₁ und µ_2` haben. Beachten Sie, dass davon ausgegangen wird, dass die Verteilungen der Grundgesamtheit normal sind, und dass die Alternativhypothese zwar zulässt, dass die Gruppen unterschiedliche Mittelwerte haben, aber davon ausgeht, dass sie die gleiche Standardabweichung haben.

Um einen Hypothesentest für dieses Szenario zu konstruieren, stellen wir zunächst fest, dass die Differenz zwischen den Mittelwerten der Grundgesamtheit genau Null ist, µ₁ - µ₁ = 0, wenn die Nullhypothese wahr ist. Folglich basiert die Teststatistik auf der Differenz zwischen den beiden Stichprobenmittelwerten. Wenn die Nullhypothese wahr ist, dann würden wir erwarten, dass X̄₁ - X̄₂ ziemlich nahe bei Null liegt. Wie wir jedoch bei unseren Tests mit einer Stichprobe (d. h. dem z-Test und dem t-Test) gesehen haben, müssen wir genau wissen, wie nahe diese Differenz bei Null liegen muss. Die Lösung des Problems ist mehr oder weniger dieselbe. Wir berechnen den Standardschätzfehler (SE), genau wie beim letzten Mal, und teilen dann die Differenz zwischen den Mittelwerten durch diese Schätzung. Unsere t-Statistik hat also die folgende Form:

t = (X̄₁ – X̄₂) / SE

Wir müssen nur noch herausfinden, wie hoch der Standardschätzfehler eigentlich ist. Das ist etwas komplizierter als bei den beiden Tests, die wir uns bisher angeschaut haben, also müssen wir es uns genauer ansehen, um zu verstehen, wie es funktioniert.

Eine „gepoolte Schätzung“ der Standardabweichung

Beim ursprünglichen t-Test nach Student wird davon ausgegangen, dass die beiden Gruppen die gleiche Standardabweichung in der Grundgesamtheit haben. Das heißt, unabhängig davon, ob die Mittelwerte der Grundgesamtheit gleich sind, nehmen wir an, dass die Standardabweichungen in der Grundgesamtheit identisch sind, σ₁ = σ₂. Da wir davon ausgehen, dass die beiden Standardabweichungen gleich sind, lassen wir die Indizes weg und bezeichnen beide mit σ. Aber wie sollten wir diese schätzen? Wie soll man eine einzelne Schätzung einer Standardabweichung konstruieren, wenn man zwei Stichproben hat? Die Antwort ist im Grunde, dass wir den Durchschnitt bilden (gewissermaßen). Genau genommen nehmen wir einen gewichteten Durchschnitt der Varianzschätzungen, den wir als gepoolte Schätzung der Varianz verwenden. Das jeder Stichprobe zugewiesene Gewicht ist gleich der Anzahl der Beobachtungen in dieser Stichprobe minus 1.

Mathematisch lässt sich dies wie folgt ausdrücken

w₁ = N₁ - 1

w₂ = N₂ - 1

Nachdem wir nun die einzelnen Stichproben gewichtet haben, berechnen wir die gepoolte Schätzung der Varianz, indem wir das gewichtete Mittel der beiden Varianzschätzungen, \({\hat\sigma_1}^2\) und \({\hat\sigma_2}^2\), bilden

\[\hat\sigma^2_p = \frac{w_1 {\hat\sigma_1}^2 + w_2 {\hat\sigma_2}^2}{w_1 + w_2}\]

Schließlich konvertieren wir die gepoolte Varianzschätzung in eine gepoolte Standardabweichungsschätzung, indem wir die Quadratwurzel ziehen.

\[\hat\sigma_p = \sqrt{\frac{w_1 {\hat\sigma_1}^2 + w_2 {\hat\sigma_2}^2}{w_1 + w_2}}\]

Und wenn Sie w₁ = N₁ - 1 und w₂ = N₂ - 1 in diese Gleichung einsetzen, erhalten Sie eine sehr hässlich aussehende Formel. Eine sehr hässliche Formel, die tatsächlich die „Standard“-Methode zur Schätzung der gepoolten Standardabweichung zu sein scheint. Es ist jedoch nicht meine bevorzugte Art, über gepoolte Standardabweichungen nachzudenken. Ich ziehe es vor, sie folgendermaßen zu betrachten. Unser Datensatz entspricht eigentlich einem Satz von N Beobachtungen, die in zwei Gruppen sortiert sind. Verwenden wir also die Notation X_ik für die Note, die der i-te Schüler im k-ten Tutorium erhalten hat. Das heißt, X₁₁ ist die Note, die der erste Schüler in Anastasias Klasse erhalten hat, X₂₁ ist ihr zweiter Schüler, und so weiter. Und wir haben zwei getrennte Gruppenmittelwerte X̄₁ und X̄₂, auf die wir uns „verallgemeinert“ mit der Schreibweise X̄_k beziehen könnten, d.h. die mittlere Note für das k-te Tutorium. So weit, so gut. Da nun jeder einzelne Student in eines der beiden Tutorien fällt, können wir seine Abweichung vom Gruppenmittelwert als Differenz beschreiben

X_ik - X̄_k

Warum also nicht einfach diese Abweichungen verwenden (d. h. das Ausmaß, in dem die Note eines jeden Schülers von der Durchschnittsnote in seinem Tutorium abweicht)? Denken Sie daran, dass eine Varianz nur der Durchschnitt einer Reihe von quadrierten Abweichungen ist, also lassen Sie uns das tun. Mathematisch könnte man es so formulieren

\[\frac{\sum_{ik} \left( X_{ik} - \bar{X}_k \right)^2}{N}\]

wobei die Schreibweise „Σ_ik“ eine einfache Art ist, zu sagen: „Berechne eine Summe, indem du alle Studenten in allen Tutorien betrachtest“, da jedes „ik“ einem Studenten entspricht.[3] Aber wie wir in Kapitel Schätzen unbekannter Größen anhand einer Stichprobe gesehen haben, führt die Berechnung der Varianz bei der wir durch N dividieren zu einer verzerrten Schätzung der Populationsvarianz. Bisher mussten wir durch N - 1 dividieren, um dies zu korrigieren. Wie ich bereits erwähnt habe, liegt der Grund für diese Verzerrung darin, dass sich die Varianzschätzung auf den Stichprobenmittelwert stützt, und in dem Maße, in dem der Stichprobenmittelwert nicht mit dem Mittelwert in der Grundgesamtheit übereinstimmt, kann dies unsere Varianzschätzung systematisch verzerren. Aber dieses Mal stützen wir uns auf zwei Stichprobenmittelwerte! Bedeutet dies, dass wir mehr Verzerrungen haben? Ja, das bedeutet es. Und bedeutet dies, dass wir jetzt durch N - 2 statt durch N - 1 dividieren müssen, um unsere gepoolte Varianzschätzung zu berechnen? Ja, natürlich.

\[\hat\sigma^2_p = \frac{\sum_{ik} \left( X_{ik} - \bar{X}_k \right)^2}{N -2}\]

Wenn Sie nun die Quadratwurzel daraus ziehen, erhalten Sie \(\hat{\sigma}_p\), die gepoolte Schätzung für die Standardabweichung. Mit anderen Worten, die Berechnung der gepoolten Standardabweichung ist nichts Besonderes. Sie unterscheidet sich nicht wesentlich von der gewöhnlichen Berechnung der Standardabweichung.

Abschließen des Tests

Unabhängig davon, welches Vorgehen gewählt wurde, haben wir nun unsere gepoolte Schätzung der Standardabweichung. Daher lasse ich nun den p-Index weg und bezeichne diese Schätzung einfach als \(\hat\sigma\). Lassen Sie uns wieder zum eigentlichen Hypothesentest zurückkehren: Der Grund für die Berechnung dieser gepoolten Schätzung war, dass wir wussten, dass sie für die Berechnung der Schätzung unseres Standardfehlers notwendig sein würde. Aber Standardfehler von was? Beim t-Test mit einer Stichprobe war es der Standardfehler des Stichprobenmittelwerts, SE(X̄), und da \(SE(X̄) = \sigma / \sqrt{N}\), sah der Nenner unserer t-Statistik auch so aus. Diesmal haben wir jedoch zwei Stichprobenmittelwerte. Und was uns besonders interessiert, ist die Differenz zwischen den beiden X̄₁ - X̄₂. Folglich ist der Standardfehler, durch den wir dividieren müssen, in Wirklichkeit der Standardfehler der Differenz zwischen den Mittelwerten.

Sofern die beiden Variablen tatsächlich dieselbe Standardabweichung haben, lautet unsere Schätzung für den Standardfehler

\[SE(\bar{X}_1 - \bar{X}_2) = \hat\sigma \sqrt{\frac{1}{N_1} + \frac{1}{N_2}}\]

und unsere t-Statistik ist daher

\[t = \frac{\bar{X}_1 - \bar{X}_2}{SE(\bar{X}_1 - \bar{X}_2)}\]

Wie wir bei unserem Test mit einer Stichprobe gesehen haben, ist die Stichprobenverteilung dieser t-Statistik eine t-Verteilung (schockierend, nicht wahr?), solange die Nullhypothese wahr ist und alle Annahmen des Tests erfüllt sind. Die Freiheitsgrade sind jedoch etwas anders. Wie üblich können wir uns vorstellen, dass die Freiheitsgrade gleich der Anzahl der Datenpunkte minus der Anzahl der Einschränkungen sind. In diesem Fall haben wir N Beobachtungen (N₁ in Stichprobe 1 und N₂ in Stichprobe 2) und 2 Einschränkungen (die Stichprobenmittelwerte). Die gesamten Freiheitsgrade für diesen Test sind also N - 2.

Durchführen des Tests in jamovi

Es überrascht nicht, dass Sie in jamovi problemlos einen t-Test für unabhängige Stichproben durchführen können. Die Ergebnisvariable für unseren Test ist die Note der Schüler (grade), und die Gruppen werden anhand der Variable tutor definiert. Es wird Sie also nicht überraschen, dass Sie in jamovi nur die entsprechende Analyse aufrufen müssen (Analyses → T-Tests → Independent Samples T-Test) und dann die Variable grade in das Feld Dependent Variables und die Variable tutor in das Feld Grouping Variable verschieben, wie in Abb. 91 gezeigt.

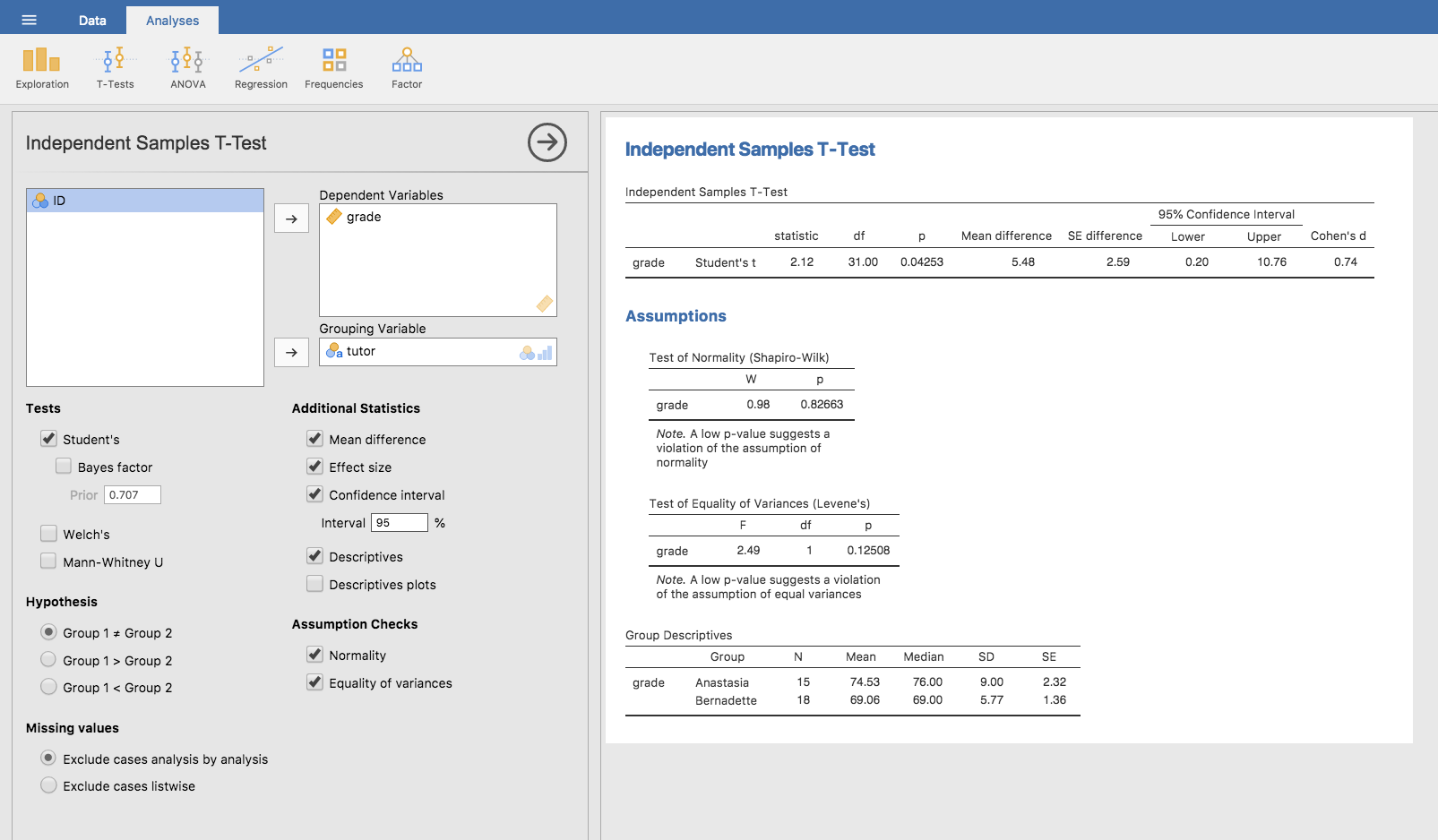
Abb. 91 Durchführen eines t-Tests für unabhängigen Stichproben in jamovi, bei dem die Optionen für die empfohlenen Ergebnisausgaben bereits gesetzt sind.

Die Ausgabe hat eine vertraute Form. Zunächst wird angegeben, welcher Test durchgeführt wurde, sowie der Name der abhängigen Variable, die Sie verwendet haben. Dann werden die Testergebnisse angezeigt. Genau wie beim letzten Mal bestehen die Testergebnisse aus einer t-Statistik, den Freiheitsgraden und dem p-Wert. Im letzten Abschnitt werden zwei Dinge angegeben: ein Konfidenzintervall und eine Effektstärke. Über Effektstärken werde ich später sprechen, über das Konfidenzintervall jetzt.

Es ist ziemlich wichtig, sich darüber im Klaren zu sein, worauf sich dieses Konfidenzintervall eigentlich bezieht. Es ist ein Konfidenzintervall für die Differenz zwischen den Gruppenmittelwerten. In unserem Beispiel hatten die Schüler von Anastasia eine Durchschnittsnote von 74,53 und die Schüler von Bernadette eine Durchschnittsnote von 69,06, so dass der Unterschied zwischen den beiden Stichprobenmittelwerten 5,48 beträgt. Natürlich kann der Unterschied zwischen den Mittelwerten der Grundgesamtheit größer oder kleiner sein als dieser Wert. Das in Abb. 91 angegebene Konfidenzintervall besagt, dass der wahre Unterschied der Mittelwerte, wenn wir diese Studie immer wieder wiederholen würden, in 95 % der Fälle zwischen 0,20 und 10,76 liegen würde. Schauen Sie noch einmal unter Schätzen eines Konfidenzintervalls nach, um sich daran zu erinnern, was Konfidenzintervalle bedeuten.

In jedem Fall ist der Unterschied zwischen den beiden Gruppen (gerade so) signifikant, so dass wir das Ergebnis in einem Text wie diesem wiedergeben könnten:

Die Durchschnittsnote in Anastasias Klasse betrug 74,5 % (Std.-abw. = 9,0), während der Mittelwert in Bernadettes Klasse bei 69,1 % (Std.-abw. = 5,8) lag. Ein t-Test für unabhängige Stichproben zeigte, dass dieser Unterschied von 5,4 % signifikant war (t(31) = 2,1, p < 0,05, CI₉₅ = [0,2, 10,8]`, d = 0,74), was darauf hindeutet, dass ein die Lernergebnisse einen echten Unterschied aufweisen.

Beachten Sie, dass ich das Konfidenzintervall und die Effektstärke in den Statistikblock aufgenommen habe. Das wird nicht immer gemacht. Zumindest sollten Sie die t-Statistik, die Freiheitsgrade und den p-Wert sehen. Sie sollten also mindestens so etwas wie das Folgende angeben: t(31) = 2,1, p < 0,05. Wenn es nach den Statistikern ginge, würde jeder auch das Konfidenzintervall und ein Effektstärke-Maß angeben, denn das sind ebenfalls nützliche Informationen. Die Realität funktioniert jedoch nicht immer so, wie Statistiker es gerne hätten. Daher sollten Sie Ihre Entscheidung davon abhängig machen, ob Sie glauben, dass es Ihren Lesern hilft, oder, wenn Sie eine wissenschaftliche Arbeit schreiben, von den redaktionellen Standards der betreffenden Zeitschrift. Einige Zeitschriften erwarten, dass Sie Effektstärken angeben, andere nicht. In einigen Wissenschaftsdisziplinen ist es üblich, Konfidenzintervalle anzugeben, in anderen nicht. Sie müssen herausfinden, was Ihre Zielgruppe erwartet. Aber nur der Klarheit halber: Ich bin der Meinung, dass Sie sowohl die Effektstärke als auch das Konfidenzintervall angeben sollten.

Positive und negative t-Werte

Bevor ich auf die Annahmen des t-Tests eingehe, möchte ich noch einen weiteren Punkt über das Verwenden von t-Tests in der Praxis ansprechen. Der erste Punkt bezieht sich auf das Vorzeichen der t-Statistik (d. h. ob es sich um eine positive oder negative Zahl handelt). Eine sehr häufige Sorge, die Studenten haben, wenn sie ihren ersten t-Test durchführen, ist, dass sie oft negative Werte für die t-Statistik erhalten und nicht wissen, wie sie diese interpretieren sollen. In der Tat ist es nicht ungewöhnlich, dass zwei Personen, die unabhängig voneinander arbeiten, fast identische Ergebnisse erhalten, mit der Ausnahme, dass eine Person einen negativen t-Wert und die andere einen positiven t-Wert hat. Unter der Annahme, dass es sich um einen zweiseitigen Test handelt, werden die p-Werte identisch sein. Bei näherer Betrachtung haben außerdem die Konfidenzintervalle die entgegengesetzten Vorzeichen haben. Das ist völlig in Ordnung. Wann immer dies geschieht, werden Sie feststellen, dass die beiden Versionen der Ergebnisse darauf zurückzuführen sind, dass leicht unterschiedliche Arten des t-Tests durchführt wurden. Was hier passiert, ist sehr einfach. Die t-Statistik, die wir hier berechnen, hat immer die Form

t = (Mittelwert 1 - Mittelwert 2) / SE

Wenn „Mittelwert 1“ größer ist als „Mittelwert 2“, ist die t-Statistik positiv, wenn „Mittelwert 2“ größer ist, ist die t-Statistik negativ. In ähnlicher Weise ist das Konfidenzintervall, das jamovi meldet, das Konfidenzintervall für die Differenz „(Mittelwert 1) minus (Mittelwert 2)“, was das Gegenteil von dem ist, was Sie erhalten würden, wenn Sie das Konfidenzintervall für die Differenz „(Mittelwert 2) minus (Mittelwert 1)“ berechnen würden.

Die Erklärung ist ziemlich simpel, wenn man darüber nachdenkt. Aber jetzt betrachten wir unseren t-Test, bei dem wir Anastasias Klasse mit Bernadettes Klasse vergleichen. Welchen sollten wir als „Mittelwert 1“ und welchen als „Mittelwert 2“ bezeichnen. Das ist willkürlich. Sie müssen jedoch wirklich einen von ihnen als „Mittelwert 1“ und den anderen als „Mittelwert 2“ bezeichnen. Es überrascht nicht, dass die Art und Weise, wie jamovi dies handhabt, ebenfalls ziemlich willkürlich ist. In früheren Versionen des Buches habe ich versucht, das zu erklären, aber nach einer Weile habe ich es aufgegeben, weil es eigentlich nicht so wichtig ist und ich es mir ehrlich gesagt selbst nie merken kann. Wenn ich ein signifikantes t-Testergebnis erhalte und herausfinden möchte, welcher Mittelwert der größere ist, versuche ich nicht, dies herauszufinden, indem ich mir die t-Statistik ansehe. Warum sollte ich mir die Mühe machen, das zu tun? Es ist töricht. Es ist einfacher, sich die tatsächlichen Gruppenmittelwerte anzusehen, da die jamovi-Ausgabe sie ebenfalls anzeigt!

Das Wichtigste ist, die t-Statistik so zu berichten, dass die Zahlen mit dem Text übereinstimmen. Angenommen, ich möchte in meinem Bericht schreiben: „Anastasias Klasse hatte bessere Noten als Bernadettes Klasse“. Die Formulierung impliziert, dass Anastasias Gruppe an erster Stelle steht, so dass es sinnvoll ist, die t-Statistik so darzustellen, als ob Anastasias Klasse der Gruppe 1 entsprechen würde. In diesem Fall würde ich schreiben

Die Klasse von Anastasia hatte bessere Noten als die Klasse von Bernadette: t(31) = 2,1, p = 0,04.

(Im wirklichen Leben würde ich die Aussage eventuell ohne das Wort „besser“ formulieren, ich hier tue es, um zu betonen, dass „besser“ positiven t-Werten entspricht). Nehmen wir andererseits an, dass in der Formulierung, die ich verwenden wollte, Bernadettes Klasse an erster Stelle aufgeführt ist. In diesem Fall ist es sinnvoller, ihre Klasse als Gruppe 1 zu behandeln, und in diesem Fall sieht der Text wie folgt aus

Die Klasse von Bernadette hatte schlechtere Noten als die Klasse von Anastasia: t(31) = -2,1, p = 0,04.

Da ich davon spreche, dass eine Gruppe „schlechtere“ Noten hat, ist es sinnvoller, die negative Form der t-Statistik zu verwenden. Das macht es einfach sauberer.

Eine letzte Sache: Bitte beachten Sie, dass Sie dies nicht für andere Arten von Teststatistiken tun können. Es funktioniert für t-Tests, aber es wäre nicht sinnvoll für χ²-Tests, F-Tests oder die meisten anderen Tests, die ich in diesem Buch behandle. Verallgemeinern Sie diesen Rat also nicht zu sehr! Ich spreche hier wirklich nur über t-Tests und nichts anderes!

Voraussetzungen für den t-Test nach Student

Wie immer stützt sich unser Hypothesentest auf einige Voraussetzungen. Wie lauten diese also? Für den Student t-Test gibt es drei Voraussetzungen, von denen wir einige bereits im Zusammenhang mit dem t-Test für eine Stichprobe gesehen haben (siehe Abschnitt Voraussetzungen für den *t*-Tests bei einer Stichprobe):

• Normalverteilung. Wie beim t-Test für eine Stichprobe wird angenommen, dass die Daten normalverteilt sind. Insbesondere wird angenommen, dass beide Gruppen normalverteilt sind. Im Abschnitt Überprüfen der Normalverteilung in einer Stichprobe wird erörtert, wie man auf Normalverteilung testet, und im Abschnitt Prüfen nicht-normalverteilter Daten mit dem Wilcoxon-Test werden wir mögliche Lösungen diskutieren.

• Unabhängigkeit. Auch hier wird davon ausgegangen, dass die Beobachtungen unabhängig voneinander erhoben werden. Im Zusammenhang mit dem Student-Test hat dies zwei Aspekte. Erstens wird angenommen, dass die Beobachtungen innerhalb jeder Stichprobe unabhängig voneinander sind (genau wie beim Test mit einer Stichprobe). Wir gehen aber auch davon aus, dass es keine stichprobenübergreifenden Abhängigkeiten gibt. Wenn sich beispielsweise herausstellt, dass Sie einige Teilnehmer in beide Versuchsbedingungen Ihrer Studie einbezogen haben (z. B. indem Sie versehentlich zuließen, dass sich dieselbe Person für verschiedene Bedingungen anmeldete), dann gibt es einige stichprobenübergreifende Abhängigkeiten, die Sie berücksichtigen müssen.

• Varianzhomogenität (auch „Homoskedastizität“ genannt). Die dritte Annahme ist, dass die Standardabweichung in der Grundgesamtheit für beide Gruppen gleich ist. Sie können diese Annahme mit dem Levene-Test testen, auf den ich später im Buch eingehe (Abschnitt Überprüfen der Annahme der Varianzhomogenität). Wenn Sie sich Sorgen machen, gibt es jedoch eine sehr einfache Lösung für diese Annahme, die ich im nächsten Abschnitt erläutern werde.

---

[1]

Es ist das Einfachste, deshalb werde ich damit anfangen.

[2]

An dieser Stelle taucht eigentlich immer die Frage auf: Was zum Teufel ist die Grundgesamtheit, auf die in diesem Fall Bezug genommen wird? Ist es die Gruppe der Studenten, die den Kurs von Dr. Harpo tatsächlich besucht (alle 33)? Die Gruppe der Personen, die den Kurs besuchen könnten (eine unbekannte Anzahl von ihnen)? Oder etwas anderes? Spielt es eine Rolle, welche der beiden Gruppen wir wählen? Es ist üblich, in einem Einführungskurs in die Verhaltensstatistik an dieser Stelle viel zu murmeln, aber da ich diese Frage jedes Jahr von meinen Studenten gestellt bekomme, werde ich eine kurze Antwort geben. Technisch gesehen spielt es tatsächlich eine Rolle. Wenn Sie Ihre Definition der Grundgesamtheit in der „realen Welt“ ändern, ändert sich auch die Stichprobenverteilung des beobachteten Mittelwerts X̄. Der t-Test beruht auf der Annahme, dass die Beobachtungen nach dem Zufallsprinzip aus einer unendlich großen Grundgesamtheit gezogen werden, und in dem Maße, in dem das wirkliche Leben nicht so ist, kann der t-Test falsch sein. In der Praxis spielt dies jedoch in der Regel keine große Rolle. Auch wenn die Annahme fast immer falsch ist, führt sie nicht zu einem pathologischen Verhalten des Tests, so dass wir dazu neigen, sie einfach zu ignorieren.

[3]

Eine korrektere Schreibweise wird im Kapitel Vergleich mehrerer Mittelwerte (einfaktorielle ANOVA) eingeführt.