Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft
Modellprüfung
Der Schwerpunkt dieses Abschnitts liegt auf der Regressionsdiagnostik, einem Begriff, der sich auf die Kunst bezieht, zu überprüfen, ob die Annahmen Ihres Regressionsmodells erfüllt wurden und herauszufinden, wie das Modell geändert werden kann, wenn die Annahmen verletzt wurden, und allgemein zu überprüfen, ob nichts „Seltsames“ vor sich geht. Ich bezeichne es aus diesem Grund als die „Kunst“ der Modellprüfung. Es ist nicht einfach. Obwohl es viele standardisierte Werkzeuge gibt, mit denen Sie die Probleme Ihres Modells diagnostizieren und vielleicht sogar beheben können (falls es eine solche Lösung gibt), müssen Sie dabei ein gewisses Maß an Urteilsvermögen walten lassen. Es ist leicht, sich in all den Details der Überprüfung dieses oder jenes Dings zu verlieren, und es ist ziemlich anstrengend, sich daran zu erinnern, was all die verschiedenen Teilaspekte sind. Dies hat den sehr unangenehmen Nebeneffekt, dass viele Leute frustriert sind. Und anstatt zu versuchen, alle Werkzeuge zu lernen, beschließen sie, keine Modellprüfung durchzuführen. Das ist besorgniserregend!
In diesem Abschnitt beschreibe ich verschiedene Dinge, die Sie tun können, um zu überprüfen, ob Ihr Regressionsmodell das tut, was es tun soll. Es deckt nicht das gesamte Spektrum der Möglichkeiten ab, die Sie untersuchen könnten. Aber es ist immer noch viel detaillierter als das, was ich viele Leute in der Praxis tun sehe, und selbst ich decke normalerweise nicht alle Möglichkeiten in meinen Statistik-Einführungskursen ab. Ich denke jedoch, dass es wichtig ist, dass Sie ein Gefühl dafür bekommen, welche Werkzeuge Ihnen zur Verfügung stehen. Also werde ich versuchen, hier ein paar davon vorzustellen. Schließlich sollte ich anmerken, dass dieser Abschnitt ziemlich stark von Fox und Weisberg (2011) geprägt ist, das Buch, das mit dem R-Paket car verbunden ist, und zum Durchführen von Regressionsanalysen in R verwendet werden kann. Das car-Paket zeichnet sich dadurch aus, dass es einige hervorragende Werkzeuge für die Regressionsdiagnose bietet, und das Buch beschreibt diese Werkzeuge in bewundernswerter Klarheit. Ich möchte nicht zu überschwänglich klingen, aber ich denke, dass Fox und Weisberg (2011) lesenswert ist, auch wenn einige der fortgeschrittenen Diagnosetechniken nur in R und nicht in jamovi verfügbar sind.
Drei Arten von Residuen
Ein wichtiger Aspekt der Regressionsdiagnostik ist die Betrachtung der Residuen. Inzwischen haben Sie wahrscheinlich eine ausreichend pessimistische Sicht auf die Statistik gebildet, um erraten zu können, dass es verschiedene Arten von Residuen gibt, die wir betrachten können, und dass dies der Grund dafür ist, weshalb wir uns so sehr um die Residuen kümmern. In diesem Abschnitt wird insbesondere auf die folgenden drei Arten von Residuen Bezug genommen: „gewöhnliche Residuen“, „standardisierte Residuen“ und „studentisierte Residuen“. Es gibt eine vierte Art, auf die in einigen der Abbildungen Bezug genommen wird, und das sind „Pearson-Residuen“. Für die Modelle, über die wir in diesem Kapitel sprechen, sind Pearson-Residuen jedoch identisch mit den gewöhnlichen Residuen.
Die erste und einfachste Art von Residuen, die uns wichtig sind, sind gewöhnliche Residuen. Dies sind die eigentlichen Roh-Residuen, über die ich in diesem Kapitel bis jetzt gesprochen habe. Das gewöhnliche Residuum ist nur die Differenz zwischen dem vorhergesagten Wert Ŷ:sub:i und dem beobachteten Wert Y:sub:i. Ich habe die Notation ε:sub:i benutzt, um auf das i-te gewöhnliche Residuum zu verweisen, und ich werde mich and diese Nomenklatur halten. In diesem Sinne haben wir die sehr einfache Gleichung:
Das ist natürlich das, was wir früher gesehen haben. Wenn ich mich nicht speziell auf eine andere Art von Residuen beziehe, sind es gewöhnliche Residuen, von denen ich spreche. Hier gibt es also nichts Neues. Ein Nachteil bei der Verwendung gewöhnlicher Residuen besteht darin, dass sie jeweils verschiedene Skalierungen haben, je nachdem, was die Ergebnisvariable ist und wie gut das Regressionsmodell angepasst ist. Das heißt, nur dann wenn Sie sich entschieden haben, ein Regressionsmodell ohne einen Interzept-Term zu erstellen, haben die gewöhnlichen Residuen einen Mittelwert von 0, aber in jedem Fall ist die Varianz ist für jede Regression unterschiedlich. In vielen Zusammenhängen, insbesondere wenn Sie nur am Verhältnis der Residuen zueinander und nicht an ihren tatsächlichen Werten interessiert sind, ist es praktisch, die standardisierten Residuen zu schätzen, die so normiert werden, dass sie eine Standardabweichung 1 haben.
Die Art und Weise, wie wir diese berechnen, besteht darin, das gewöhnlichen Residuum durch eine Schätzung der Standardabweichung dieser Residuen in der Grundgesamtheit zu dividieren. Aus technischen Gründen… unverständlich… lautet die Formel dafür
wobei \(\hat{\sigma}\) in diesem Zusammenhang die geschätzte Standardabweichung der gewöhnlichen Residuen und h:sub:‘i‘ der „Dach-Wert“ der i-ten Beobachtung ist. Ich habe die Dach-Werte noch nicht erklärt (aber keine Angst,[1] das kommt in Kürze), also wird das nicht viel Sinn machen. Im Moment reicht es aus, die standardisierten Residuen so zu interpretieren, als hätten wir die gewöhnlichen Residuen in z-Werte umgewandelt. Tatsächlich entspricht das mehr oder weniger die Wahrheit, es ist nur so, dass wir das auf eine ein bisschen ausgefallenere Art machen.
Die dritte Art von Residuen sind Studentisierte Residuen (auch „jackknifed residuals“ genannt). Sie sind noch schicker als standardisierte Residuen. Auch hier besteht die Idee darin, das gewöhnlichen Residuum zu nehmen und durch eine bestimmte Größe zu dividieren, um eine standardisierte Schätzung des Residuums zu erhalten.
Die Formel für das Durchführen der Berechnungen ist diesmal etwas anders
Beachten Sie, dass unsere Schätzung der Standardabweichung hier als \(\hat{\sigma}_{(-i)}\). Dies entspricht der Schätzung der Standardabweichung der Residuen, die Sie erhalten hätten, wenn Sie die i-te Beobachtung einfach aus dem Datensatz gelöscht hätten. Das klingt nach etwas, was zu berechnen ein Albtraum ist, da es zu sagen scheint, dass Sie N neue Regressionsmodelle ausführen müssten (wo selbst ein moderner Computer ein wenig murren würde, besonders wenn Sie einen großen Datensatz haben). Glücklicherweise hat eine schrecklich kluge Person gezeigt, dass diese Schätzung der Standardabweichung tatsächlich durch die folgende Gleichung möglich ist:
Ist das nicht ein krönender Abschluss?
Bevor ich fortfahre, sollte ich darauf hinweisen, dass Sie diese Residuen nicht oft selbst berechnen müssen, obwohl sie im Mittelpunkt fast jeder Regressionsdiagnostik stehen. Meistens übernehmen die verschiedenen Optionen, welche die Diagnose oder das Prüfen von Voraussetzungen durchführen, diese Berechnungen für Sie. Trotzdem ist es gut zu wissen, wie man diese Berechnungen selbst durchführen könnte, falls man jemals eine Diagnostik durchführen möchte, die durch keine der Standardmethoden abgedeckt wird.
Drei Arten von anomalen Daten
Eine Gefahr, auf die Sie bei linearen Regressionsmodellen stoßen können, ist, dass Ihre Analyse möglicherweise unverhältnismäßig empfindlich auf eine kleine Anzahl von „ungewöhnlichen“ oder „anomalen“ Beobachtungen reagiert. Ich habe diese Idee bereits im Abschnitt Verwenden von Boxplots zum Identifizieren von Ausreißern vorgestellt, wo Ausreißer automatisch durch die Option Box plot unter Exploration → Descriptives identifiziert wurden. Diesmal müssen wir aber viel präziser sein. Im Zusammenhang mit der linearen Regression gibt es drei konzeptuell verschiedene Arten, um eine Beobachtung als „anomal“ zu klassifizieren. Alle drei sind interessant, aber sie haben ziemlich unterschiedliche Auswirkungen auf Ihre Analyse.
Die erste Art von ungewöhnlichen Beobachtungen sind Ausreißer. Ein Ausreißer ist (in diesem Zusammenhang) eine Beobachtung, die sich stark von dem unterscheidet, was das Regressionsmodell vorhersagt. Ein Beispiel ist in Abb. 122 dargestellt. In der Praxis operationalisieren wir dieses Konzept, indem wir sagen, dass ein Ausreißer eine Beobachtung ist, die einen sehr großes studentisiertes Residuum hat, εi*. Ausreißer sind interessant: Ein Ausreißer könnte fehlerhaften Daten entsprechen, z.B. weil Variablen falsch im Datensatz aufgezeichnet wurden, oder auf Grund von Fehlern bei der Dateneingabe. Beachten Sie, dass Sie eine Beobachtung nicht wegwerfen sollten, nur weil es sich um einen Ausreißer handelt. Aber die Tatsache, dass es sich um einen Ausreißer handelt, ist oft ein Hinweis, sich diesen Fall genauer anzusehen und herauszufinden, warum er sich so stark von den übrigen Fällen unterscheidet.
Abb. 122 Darstellung von Ausreißern: Die gepunkteten Linien stellen die Regressionsgeraden dar, welche ohne die anomale Beobachtung geschätzt worden wäre, und das entsprechende Residuum (d.h. das studentisierte Residuum). Die durchgezogene Linie zeigt die Regressionsgerade mit der eingeschlossenen anomalen Beobachtung. Der Ausreißer hat einen ungewöhnlichen Wert für das Ergebnis (Position auf der Y-Achse), aber nicht für den Prädiktor (Position auf der X-Achse) und liegt weit von der Regressionsgerade entfernt.
Abb. 123 Illustration von Hebelpunkten: Die anomale Beobachtung ist in diesem Fall sowohl in Bezug auf den Prädiktor (x-Achse) als auch auf das Ergebnis (y-Achse) ungewöhnlich, aber diese Ungewöhnlichkeit stimmt stark mit dem Korrelationsmuster überein, das zwischen den anderen Beobachtungen besteht. Die Beobachtung liegt sehr nahe an der Regressionsgerade und verzerrt sie nicht.
Die zweite Möglichkeit, wie eine Beobachtung ungewöhnlich sein kann, ist, wenn sie eine hohe Hebelwirkung hat. Das passiert, wenn sich die Beobachtung stark von allen anderen Beobachtungen unterscheidet. Dies muss nicht unbedingt einem großen Residuum entsprechen. Wenn die Beobachtung bei allen Variablen auf genau die gleiche Weise ungewöhnlich ist, kann sie tatsächlich sehr nahe an der Regressionsgeraden liegen. Ein Beispiel dafür ist in Abb. 123 dargestellt. Die Hebelwirkung einer Beobachtung wird in Bezug auf ihren Dach-Wert operationalisiert, der normalerweise hi geschrieben wird. Die Formel für den Dach-Wert ist ziemlich kompliziert,[2] aber die Interpretation ist es nicht: hi ist ein Maß dafür, inwieweit die i-te Beobachtung „kontrolliert“ hat, wie die Regressionsgerade verläuft.
Wenn eine Beobachtung in Bezug auf die Prädiktorvariablen weit von den anderen entfernt liegt, hat sie im Allgemeinen einen großen Dach-Wert (als grobe Richtlinie gilt, dass eine hohe Hebelwirkung vorliegt, wenn der Dach-Wert mehr als das 2- bis 3-fache des Durchschnitts beträgt; aber beachten Sie, dass die Summe der Dach-Werte auf K + 1 beschränkt ist). Punkte mit großer Hebelwirkung sind ebenfalls einen genaueren Blick wert, aber sie geben viel weniger Anlass zur Sorge, es sei denn, sie sind zusätzlich Ausreißer.
Abb. 124 Veranschaulichung von Punkten mit hohem Einfluss: In diesem Fall ist die anomale Beobachtung in Bezug auf die Prädiktorvariable (x-Achse) höchst ungewöhnlich und liegt weit von der Regressionsgeraden entfernt. Als Folge ist die Regressionsgerade stark verzerrt, obwohl (in diesem Fall) die anomale Beobachtung in Bezug auf die Ergebnisvariable (y-Achse) durchaus typisch ist.
Dies bringt uns zu unserem dritten Maß der Ungewöhnlichkeit, dem Einfluss einer Beobachtung. Eine Beobachtung mit hohem Einfluss ist ein Ausreißer mit hoher Hebelwirkung. Das heißt, es ist eine Beobachtung, die sich in gewisser Hinsicht von allen anderen stark unterscheidet und auch weit von der Regressionsgeraden entfernt liegt. Dies wird in Abb. 124 veranschaulicht. Beachten Sie den Kontrast zu den beiden vorherigen Abbildungen. Ausreißer verändern die Regressionsgerade nicht stark und Punkte mit hoher Hebelwirkung ebenfalls nicht. Aber etwas, das sowohl ein Ausreißer ist, als auch eine hohe Hebelwirkung hat, hat einen großen Einfluss auf die Regressionsgerade. Deshalb nennen wir diese Punkte solche mit hohem Einfluss, und deshalb sind sie unsere größte Sorge. Wir operationalisieren den Einfluss durch ein Maß, welches als Cook-Distanz bekannt ist.
Beachten Sie, dass dies eine Multiplikation von etwas ist, das beschreibt, in welchem Maß eine Beobachtung ein Ausreißer ist (links), und etwas, das die Hebelwirkung dieser Beobachtung misst (rechts).
Um eine große Cook-Distanz zu haben, muss eine Beobachtung ein ziemlich wesentlicher Ausreißer sein und eine hohe Hebelwirkung haben. Als grobe Richtlinie wird eine Cooks Distanz von mehr als 1 oft als groß angesehen (das ist, was ich normalerweise als Faustregel verwende).
In jamovi können Informationen zur Cook-Distanz berechnet werden, indem Sie auf die Cook’s Distance-Checkbox in den Optionen Assumption Checks → Data Summary setzen. Wenn Sie dies tun, erhalten Sie für das multiple Regressionsmodell, das wir in diesem Kapitel als Beispiel verwendet haben, die Ergebnisse, die in Abb. 125zu sehen sind.
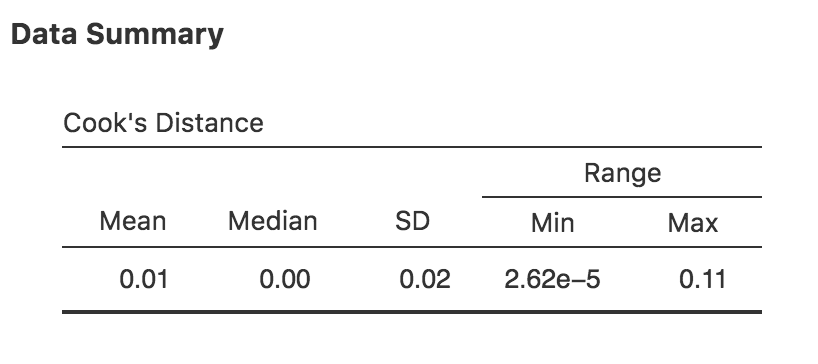
Abb. 125 jamovi-Ausgabe mit einer Tabelle mit der Cook-Distanz-Statistik
Sie können sehen, dass in diesem Beispiel der mittlere Wert für die Cook-Distanz 0,01 beträgt und der Wertebereich zwischen 0,00000262 und 0,11 liegt. Dies ist also ein Stück unterhalb der oben erwähnten Faustregel, nach der eine Cook-Distanz von über 1 als groß gilt.
Die naheliegende Frage, die Sie als Nächstes stellen sollten, lautet: Was sollten Sie tun, wenn Sie große Werte für die Cook-Distanz erhalten? Wie immer gibt es keine feste Regel. Wahrscheinlich ist das Erste, was Sie tun sollten, zu versuchen, die Regression ohne den Ausreißer mit der größten Cook-Distanz durchzuführen[3] und zu sehen, wie sich das auf die Modellleistung und die Regressionskoeffizienten auswirkt. Wenn sie sich wesentlich unterscheiden, sollten Sie Ihren Datensatz und Ihre Notizen während des Durchführens Ihrer Studie genauer ansehen. Versuchen Sie herauszufinden, warum dieser Datenpunkt sich so sehr von den übrigen unterscheidet. Wenn Sie davon überzeugt sind, dass nur dieser eine Datenpunkt Ihre Ergebnisse stark verzerrt, sollten Sie erwägen, ihn auszuschließen. Das ist aber alles andere als ideal, solange Sie nicht eine solide Erklärung dafür haben, warum sich dieser spezielle Fall qualitativ von den anderen unterscheidet und es daher verdient hat, separat behandelt zu werden.
Überprüfen der Normalverteilung der Residuen
Wie viele der statistischen Werkzeuge, die wir in diesem Buch besprochen haben, beruhen auch Regressionsmodelle auf der Annahme einer Normalverteilung. In diesem Fall gehen wir davon aus, dass die Residuen normalverteilt sind. Als Erstes können wir mit der Option Assumption Checks → Q-Q plot of residuals ein QQ-Diagramm zeichnen.
Die Ausgabe findet sich in Abb. 126 und zeigt die standardisierten Residuen als Funktion ihrer theoretischen Quantile gemäß dem Regressionsmodell.
Abb. 126 Diagramm der theoretischen Quantile gemäß dem Modell vs. der Quantile der standardisierten Residuen, erstellt mit jamovi
Eine andere Frage, die wir überprüfen sollten, ist die Beziehung zwischen den durch das Modell vorhergesagten Werten und den Residuen selbst. Wir können jamovi mit dem Setzen der Option Residuals Plots auffordern, ein Streudiagramm für jede Prädiktorvariable, die Ergebnisvariable und die durch das Modell vorhergesagten Werten im Vergleich zu den Residuen zu erstellen, wie in Abb. 127 zu sehen. In diesen Diagrammen suchen wir nach einer ziemlich gleichmäßigen Verteilung der „Punkte“, ohne dass eine Konzentration oder ein klares Muster der „Punkte“ zu erkennen wäre. Wenn man sich die Diagramme ansieht, gibt es nichts besonders Besorgniserregendes, da die Punkte ziemlich gleichmäßig über das gesamte Diagramm verteilt sind. Es mag eine gewisse Konzentration in den beiden Diagrammen auf der rechten Seite geben, aber dies ist nicht besonders ausgeprägt und wahrscheinlich nicht wert, sich Sorgen zu machen.
Abb. 127 Streudiagramme der Residuen, in Jamovi erstellt
Wenn die Diagramme Grund zur Bekümmerung geben, dann besteht eine mögliche Lösung für dieses Problem (und viele andere) darin, eine oder mehrere der Variablen zu transformieren. Wir haben die Grundlagen der Variablentransformation in den Abschnitten Transformieren und Umkodieren einer Variablen und Mathematische Funktionen und Operationen besprochen. Ich möchte aber hier besonders auf eine zusätzliche Möglichkeit hinweisen, die ich zuvor nicht vollständig erklärt habe: die Box-Cox-Transformation.
Die Box-Cox-Funktion ist ziemlich einfach und wird sehr häufig verwendet.
für alle Werte von λ außer λ = 0. Wenn λ = 0 ist, nehmen wir einfach den natürlichen Logarithmus (d. h. ln(x)).
Sie können sie mit der BOXCOX-Funktion im Compute-Variablenbildschirm in jamovi berechnen.
Prüfen auf Kollinearität
Die letzte Art von Regressionsdiagnose, die ich in diesem Kapitel erörtern werde, ist die Verwendung von Varianzinflationsfaktoren (VIFs). Diese sind nützlich, um festzustellen, ob die Prädiktoren in Ihrem Regressionsmodell zu stark miteinander korreliert sind. Jedem Prädiktor Xk im Modell ist ein Varianz-Inflationsfaktor zugeordnet.
Die Formel für den k-ten VIF lautet:
wobei sich R²(-k) auf den R-Quadratwert bezieht, den Sie erhalten würden, wenn Sie eine Regression mit Xk als Ergebnisvariable und allen anderen Variablen in X als Prädiktoren durchführen würden. Die Idee dabei ist, dass R²(-k) ein sehr gutes Maß dafür ist, inwieweit Xk mit allen anderen Variablen im Modell korreliert ist (d.h. durch die übrigen Variablen erklärt wird).
Die Quadratwurzel des VIF ist ziemlich einfach interpretierbar. Es sagt Ihnen, wie viel breiter das Konfidenzintervall für den entsprechenden Koeffizienten bk ist, relativ zu dem, was Sie erwartet hätten, wenn die Prädiktoren alle unkorreliert miteinander gewesen wären. Wenn Sie nur zwei Prädiktoren haben, werden die VIF-Werte immer gleich sein, wie wir sehen können, wenn wir in jamovi die Collinearity-Checkbox in den Optionen unter Regression → Assumption Checks setzen. Sowohl für dani.sleep als auch für baby.sleep beträgt der VIF 1,65. Und da 1,28 die Quadratwurzel von 1,65 ist, sehen wir, dass die Korrelation zwischen unseren beiden Prädiktoren kein großes Problem verursacht.
Um ein Gefühl dafür zu vermitteln, wie wir zu einem Modell mit größeren Kollinearitätsproblemen kommen könnten, nehmen wir an, ich würde ein viel weniger interessantes Regressionsmodell ausführen. Dabei würde ich versuchen, den day vorherzusagen, an dem die Daten gesammelt wurden, und alle übrigen Variablen im Datensatz als Prädiktoren verwenden. Um zu sehen, warum dies problematisch wäre, werfen wir einen Blick auf die Korrelationsmatrix für die vier Variablen:
dani.sleep baby.sleep dani.grump day
dani.sleep 1.00000000 0.62794934 -0.90338404 -0.09840768
baby.sleep 0.62794934 1.00000000 -0.56596373 -0.01043394
dani.grump -0.90338404 -0.56596373 1.00000000 0.07647926
day -0.09840768 -0.01043394 0.07647926 1.00000000
Wir haben einige ziemlich hohe Korrelationen zwischen einigen unserer Prädiktorvariablen. Wenn wir das Regressionsmodell ausführen und uns die VIF-Werte ansehen, sehen wir, dass die Kollinearität eine Menge Unsicherheit in Bezug auf die Koeffizienten verursacht. Führen Sie zuerst die Regression aus, wie in Abb. 128 gezeigt, und Sie können anhand der VIF-Werte sehen, dass eine deutliche Kollinearität vorliegt.
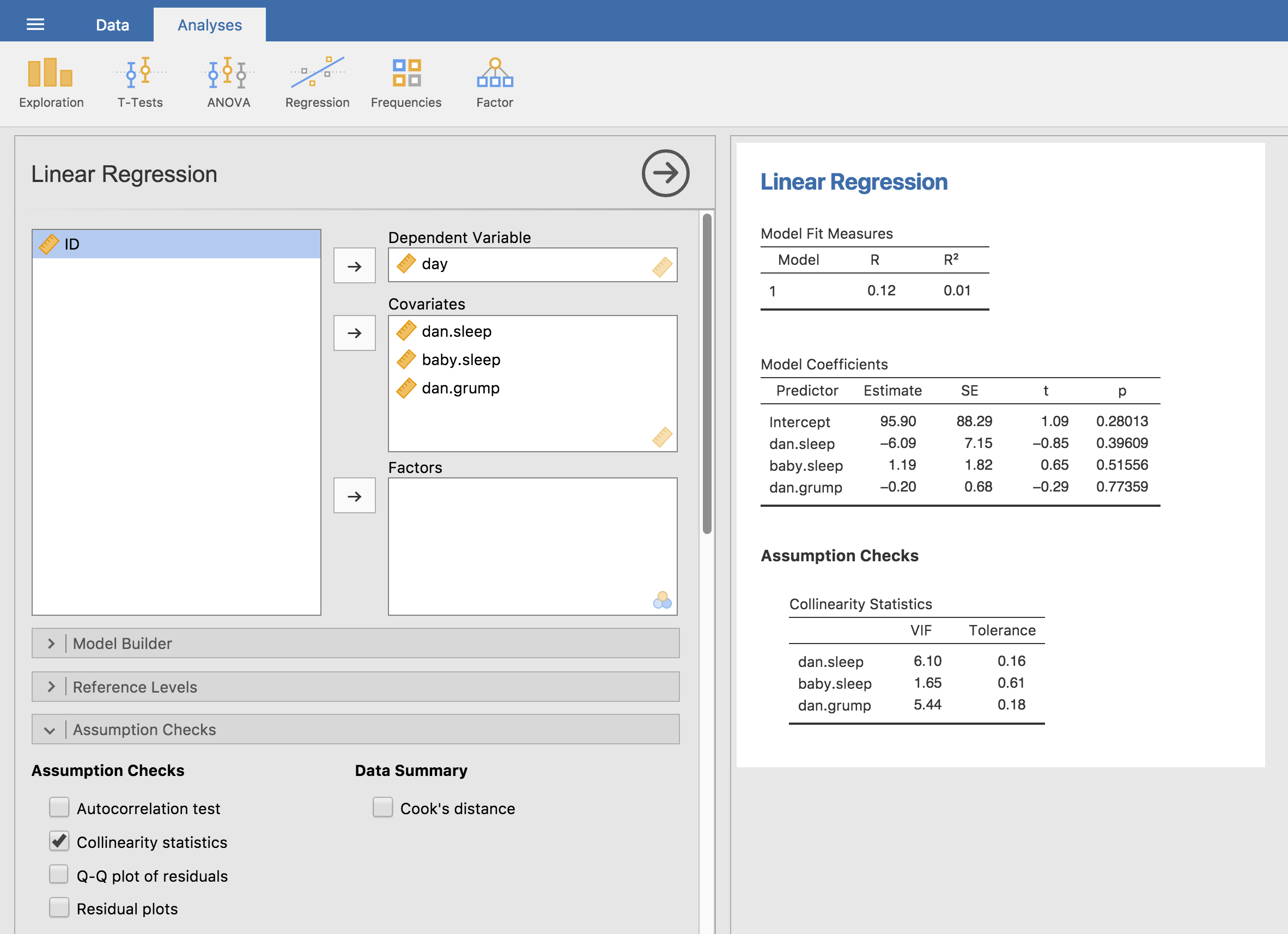
Abb. 128 Kollinearitätsstatistik für die multiple Regression, erstellt in jamovi