Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft
Korrelationen
In diesem Abschnitt werden wir darüber sprechen, wie die Beziehungen zwischen Variablen in den Daten beschrieben werden können. Zu diesem Zweck wollen wir vor allem über die Korrelation zwischen den Variablen sprechen. Aber zuerst brauchen wir einige Daten.
Die Daten
Variable |
Min. |
Max. |
Mittelwert |
Median |
Std.-abw. |
IQR |
|---|---|---|---|---|---|---|
Danis Übellaunigkeit |
41 |
91 |
63.71 |
62 |
10.05 |
14 |
Dani’s Stunden mit Schlaf |
4.84 |
9.00 |
6.97 |
7.03 |
1.02 |
1.45 |
Stunden mit Schlaf von Dani’s Sohn |
3.25 |
12.07 |
8.05 |
7.95 |
2.07 |
3.21 |
Wenden wir uns einem Thema zu, das allen Eltern am Herzen liegt: dem Schlaf. Der Datensatz, den wir verwenden werden, ist fiktiv, basiert aber auf realen Ereignissen. Angenommen, ich möchte herausfinden, wie sehr die Schlafgewohnheiten meines kleinen Sohnes meine Stimmung beeinflussen. Nehmen wir an, ich kann meine Übellaunigkeit auf einer Skala von 0 (überhaupt nicht schlecht gelaunt) bis 100 (so schlecht gelaunt wie sehr, sehr übellaunige ältere Menschen) sehr genau einschätzen. Und nehmen wir weiter an, dass ich meine Übellaunigkeit, mein Schlafverhalten und das Schlafverhalten meines Sohnes 100 Tage lang gemessen habe. Die Daten sind im Datensatz parenthood gespeichert, der vier Variablen enthält: dani.sleep, baby.sleep, dani.grump und day.
Als Nächstes werfe ich einen Blick auf einige grundlegende deskriptive Statistiken und, um eine grafische Darstellung zu geben, wie jede der drei interessanten Variablen aussieht, zeigt Abb. 106 Histogramme. Eine Anmerkung: Nur weil jamovi Dutzende verschiedener Statistiken berechnen kann, heißt das nicht, dass man sie alle ausgeben sollte. Würde ich über diese Daten berichten wollen, würde ich wahrscheinlich die Statistiken auswählen, die für mich (und meine angenommene Leserschaft) am interessantesten sind, und sie dann in eine einfache Tabelle wie Tab. 13 einfügen.[1] Das ist immer eine gute Vorgehensweise. Beachten Sie auch, dass ich nicht genug Schlaf bekomme. Das ist nicht empfehlenswert, aber andere Eltern sagen mir, dass das ziemlich normal ist.
Abb. 106 Histogramme für die drei interessierenden Variablen aus dem Datensatz parenthood
Die Stärke und Richtung einer Beziehung
Wir können Streudiagramme zeichnen, die uns einen allgemeinen Eindruck davon vermitteln, wie eng zwei Variablen miteinander zusammenhängen. Idealerweise sollten wir jedoch etwas mehr darüber aussagen, als das. Vergleichen wir zum Beispiel die Beziehung zwischen dani.sleep und dani.grump (Abb. 107, links) mit der zwischen baby.sleep und dani.grump (Abb. 107, rechts). Wenn man sich diese beiden Diagramme nebeneinander ansieht, wird deutlich, dass die Beziehung qualitativ in beiden Fällen die gleiche ist: mehr Schlaf bedeutet bessere Laune! Es ist jedoch auch ziemlich offensichtlich, dass die Beziehung zwischen dani.sleep und dani.grump stärker ist als die Beziehung zwischen baby.sleep und dani.grump. Das Diagramm auf der linken Seite ist „ordentlicher“ als das auf der rechten Seite. Wenn Sie meine Stimmung vorhersagen wollen, hilft es Ihnen ein wenig, wenn Sie wissen, wie viele Stunden mein Sohn geschlafen hat. Es ist stattdessen hilfreicher, wenn Sie wissen, wie viele Stunden ich geschlafen habe.
Abb. 107 Streudiagramme, die das Verhältnis zwischen dani.sleep und dani.grump (links) und das Verhältnis zwischen baby.sleep und dani.grump (rechts) zeigen.
Betrachten wir im Gegensatz dazu die beiden in Abb. 108 dargestellten Streudiagramme. Wenn wir das Streudiagramm von baby.sleep vs. dani.grump (links) mit dem Streudiagramm von baby.sleep vs. dani.sleep (rechts) vergleichen, ist die Gesamtstärke der Beziehung die gleiche, aber die Richtung ist anders. Das heißt, wenn mein Sohn mehr schläft, bekomme ich mehr Schlaf (positive Beziehung, rechts). Gleichzeitig bin ich weniger schlecht gelaunt, wenn er mehr schläft (negative Beziehung, links).
Abb. 108 Streudiagramme, die das Verhältnis zwischen baby.sleep und dani.grump (links) sowie das Verhältnis zwischen baby.sleep und dani.sleep (rechts) zeigen.
Der Korrelationskoeffizient
Wir können diese Ideen etwas deutlicher machen, indem wir die Idee eines Korrelationskoeffizienten (oder, genauer gesagt, des Pearsonschen Korrelationskoeffizienten) einführen, der traditionell als r bezeichnet wird. Der Korrelationskoeffizient zwischen zwei Variablen X und Y (manchmal als rXY bezeichnet), den wir im nächsten Abschnitt genauer definieren werden, ist ein Maß, das von -1 bis 1 variiert. Wenn r = -1 ist, bedeutet dies, dass wir eine perfekte negative Beziehung haben, und wenn r = 1 ist, bedeutet dies, dass wir eine perfekte positive Beziehung haben. Wenn r = 0 ist, gibt es überhaupt keine Beziehung. Unter Abb. 109 finden Sie mehrere Diagramme, die zeigen, wie die verschiedenen Korrelationen aussehen können.
Abb. 109 Veranschaulichung der Auswirkungen einer Änderung der Stärke und Richtung einer Korrelation. In der linken Spalte sind die Korrelationen 0,00, 0,33, 0,67 und 1,00 dargestellt, in der rechten Spalte die Korrelationen 0,00, -0,33, -0,67 und -1,00.
Die Formel für den Pearsonschen Korrelationskoeffizienten kann auf verschiedene Arten geschrieben werden. Meiner Meinung nach ist es am einfachsten, die Formel in zwei Schritte aufzuteilen. Führen wir zunächst die Idee einer Kovarianz ein. Die Kovarianz zwischen zwei Variablen X und Y ist eine Verallgemeinerung des Begriffs der Varianz und stellt eine mathematisch einfache Möglichkeit dar, die Beziehung zwischen zwei Variablen zu beschreiben, die für den Menschen nicht sehr informativ ist
Da wir eine Größe, die von X abhängt, mit einer Größe, die von Y abhängt, multiplizieren (d. h. das „Produkt“ davon nehmen) und dann den Mittelwert bilden, [2] können Sie sich die Formel für die Kovarianz als „durchschnittliches Kreuzprodukt“ zwischen X und Y vorstellen.
Die Kovarianz hat die nützliche Eigenschaft, dass die Kovarianz genau Null ist, wenn X und Y völlig unabhängig voneinander sind. Wenn die Beziehung zwischen ihnen positiv ist (im Sinne von Abb. 109), dann ist auch die Kovarianz positiv, und wenn die Beziehung negativ ist, dann ist auch die Kovarianz negativ. Mit anderen Worten: Die Kovarianz gibt die grundlegende qualitative Idee der Korrelation wieder. Leider ist die Kovarianz für Rohdaten nicht einfach zu interpretieren, da sie von den Einheiten abhängt, in denen X und Y ausgedrückt werden. Schlimmer ist, dass die tatsächlichen Einheiten, in denen die Kovarianz ausgedrückt wird, wirklich seltsam sind. Wenn sich zum Beispiel X auf die Variable dani.sleep (Einheit: Stunden) und Y auf die Variable dani.grump (Einheit: Übellaunigkeit) bezieht, dann sind die Einheiten für ihre Kovarianz „Stunden × Übellaunigkeit“. Und ich habe keinen blassen Schimmer, was das überhaupt bedeuten soll.
Der Pearson-Korrelationskoeffizient r behebt dieses Interpretationsproblem, indem er die Kovarianz standardisiert, und zwar auf ziemlich genau dieselbe Weise, wie der z-Score eine Rohdaten-Variable standardisiert, indem er durch die Standardabweichung dividiert wird. Da wir jedoch zwei Variablen haben, die zur Kovarianz beitragen, funktioniert die Standardisierung nur, wenn wir durch beide Standardabweichungen dividieren.[3] Das bedeutet, dass die Korrelation zwischen X und Y wie folgt geschrieben werden kann:
Durch die Standardisierung der Kovarianz bleiben nicht nur die zuvor besprochenen nützlichen Eigenschaften der Kovarianz erhalten, sondern die tatsächlichen Werte für r liegen auf einer sinnvollen Skala: r = 1 bedeutet eine perfekte positive Beziehung und r = -1 bedeutet eine perfekte negative Beziehung. Auf diesen Punkt werde ich später im Unterabschnitt Interpretation einer Korrelation noch etwas näher eingehen. Zuvor wollen wir uns jedoch ansehen, wie Korrelationen in jamovi berechnet werden.
Berechnen von Korrelationen in jamovi
Das Berechnen von Korrelationen in jamovi erfolgt durch Klicken auf die Schaltfläche Regression → Correlation Matrix. Übertragen Sie alle vier kontinuierlichen Variablen in das Feld auf der rechten Seite, um die Ausgabe in Abb. 110 zu erhalten.
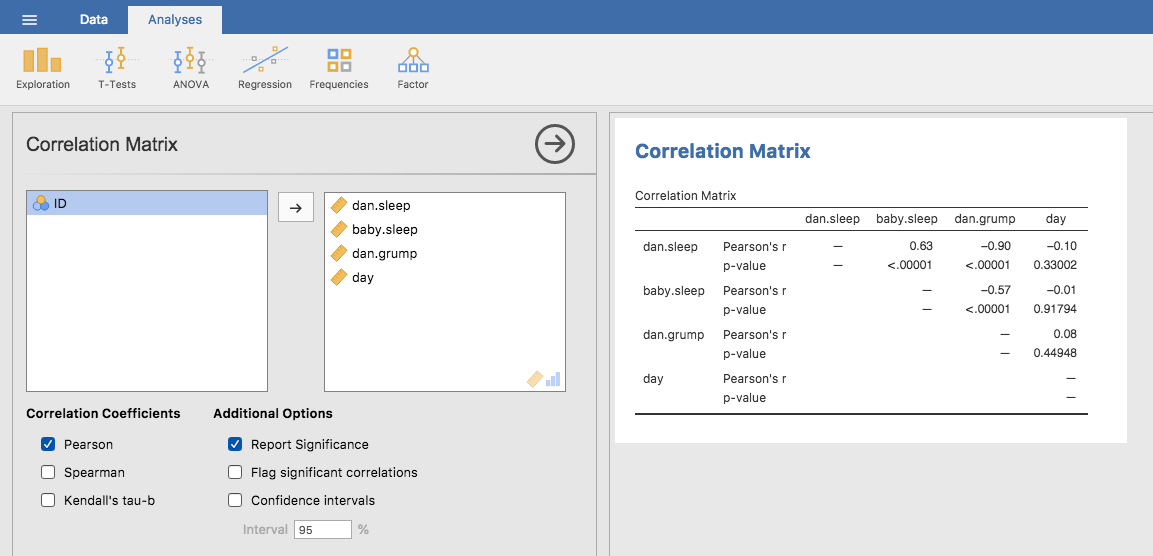
Abb. 110 jamovi-Screenshot mit den Korrelationen zwischen den Variablen im Datensatz parenthood
Interpretieren einer Korrelation
Natürlich gibt es im wirklichen Leben nicht viele Korrelationen von 1. Wie sollten Sie also eine Korrelation von, sagen wir, r = 0,4 interpretieren? Die ehrliche Antwort ist, dass es wirklich davon abhängt, wofür Sie die Daten verwenden wollen und wie stark die Korrelationen in Ihrem Arbeitsbereich typischerweise sind. Ein befreundeter Ingenieur behauptete einmal, dass jede Korrelation unter 0,95 völlig unbrauchbar ist (ich glaube, er hat übertrieben, selbst für den Ingenieurbereich). Andererseits gibt es selbst in der Psychologie Fälle, in denen man wirklich so starke Korrelationen erwarten sollte. So ist zum Beispiel einer der Benchmark-Datensätze, mit denen Theorien darüber getestet werden, wie Menschen Ähnlichkeiten beurteilen, so sauber, dass jede Theorie, die nicht mindestens eine Korrelation von 0,9 erreicht, als nicht erfolgreich gilt. Wenn man jedoch nach (sagen wir) elementaren Korrelaten der Intelligenz sucht (z. B. Inspektionszeit, Reaktionszeit), ist man sehr gut dran, wenn man eine Korrelation von über 0,3 erreicht. Kurz gesagt, die Interpretation einer Korrelation hängt stark vom Kontext ab. Die groben Richtwerte in Tab. 14 sind jedoch ein guter Ausgangspunkt.
Korrelation |
Stärke |
Richtung |
|---|---|---|
-1,0 bis -0,9 |
Sehr stark |
Negativ |
-0,9 bis -0,7 |
Stark |
Negativ |
-0,7 bis -0,4 |
Mäßig |
Negativ |
-0,4 bis -0,2 |
Schwach |
Negativ |
-0,2 bis 0,0 |
Unbedeutend |
Negativ |
0,0 bis 0,2 |
Unbedeutend |
Positiv |
0,2 bis 0,4 |
Schwach |
Positiv |
0,4 bis 0,7 |
Mäßig |
Positiv |
0,7 bis 0,9 |
Stark |
Positiv |
0,9 bis 1,0 |
Sehr stark |
Positiv |
Abb. 111 Das Anscombe-Quartett: Alle vier Variablenpaare weisen eine Pearson-Korrelation von r = 0,816 auf, unterscheiden sich aber qualitativ deutlich voneinander.
Man kann nicht oft genug betonen, dass man sich immer das Streudiagramm ansehen sollte, bevor man seine Daten interpretiert. Eine Korrelation bedeutet möglicherweise nicht das, was Sie denken. Das klassische Beispiel hierfür ist das „Anscombe-Quartett“ (Anscombe, 1973), eine Sammlung von vier Variablenpaaren, jeweils X und Y. Für alle vier Variablenpaare beträgt der Mittelwert für X = 9 und der Mittelwert für Y = 7,5. Die Standardabweichung ist für alle X-Variablen fast identisch, ebenso wie die für die Y Variablen. Und in jedem Fall beträgt die Korrelation zwischen X und Y * r* = 0,816`. Sie können dies selbst überprüfen, indem Sie den Datensatz anscombe benutzen.
Man sollte meinen, dass diese vier Datensätze einander ziemlich ähnlich sehen. Das tun sie aber nicht. Wenn wir die Streudiagramme X gegen Y für alle vier Variablenpaare zeichnen, wie in Abb. 111 gezeigt, sehen wir, dass sich alle vier deutlich voneinander unterscheiden. Die Lektion hier, die so viele Leute im wirklichen Leben zu vergessen scheinen, ist Ihre Rohdaten immer grafisch darzustellen (Kapitel Diagramme erstellen).
Rangkorrelationen nach Spearman
Der Pearson-Korrelationskoeffizient ist in vielerlei Hinsicht nützlich, hat aber auch seine Schwächen. Ein Problem fällt besonders auf: Er misst die Stärke der linearen Beziehung zwischen zwei Variablen. Mit anderen Worten, es ist ein Maß dafür, inwieweit die Daten alle auf eine einzige, perfekt gerade Linie fallen. Oft ist dies eine ziemlich gute Annäherung an das, was wir meinen, wenn wir von „Beziehung“ sprechen, und daher ist das Berechnen einer Pearson-Korrelation oft eine gute Idee. Manchmal ist dies jedoch nicht der Fall.
Eine sehr häufige Situation, in der die Pearson-Korrelation nicht ganz das Richtige ist, ergibt sich, wenn ein Anstieg einer Variablen X sich tatsächlich in einem Anstieg einer anderen Variablen Y widerspiegelt, aber die Art der Beziehung nicht unbedingt linear ist. Ein Beispiel hierfür wäre die Beziehung zwischen Aufwand und Belohnung beim Lernen für eine Prüfung. Wenn Sie sich überhaupt nicht anstrengen (X), um ein Fach zu lernen, sollten Sie 0 % als Note erwarten (Y). Ein wenig Anstrengung wird jedoch eine massive Verbesserung bewirken. Wenn Sie einfach nur zu den Vorlesungen kommen, lernen Sie schon eine ganze Menge, und wenn Sie einfach nur zum Unterricht erscheinen und ein paar Dinge aufschreiben, könnte Ihre Note auf 35 % steigen, und das alles ohne große Anstrengung. Am anderen Ende der Skala hat man jedoch nicht denselben Effekt. Wie jeder weiß, braucht es viel mehr Aufwand, um eine Note von 90 % zu erreichen, als für eine Note von 55 %. Das bedeutet, dass bei Daten, die sich mit Lernaufwand und Noten befassen, die Wahrscheinlichkeit groß ist, dass Pearson-Korrelationen irreführend sind.
Betrachten Sie zur Veranschaulichung die in Abb. 112 gezeigten Daten, die für 10 Studenten das Verhältnis zwischen dem Arbeitseinsatz für einen Kurs (in h) und der Note zeigen. Das Kuriose an diesem (fiktiven) Datensatz ist, dass eine Erhöhung des Aufwands immer die Note erhöht. Das kann sehr viel oder wenig sein, aber eine Erhöhung des Arbeitsaufwands führt nie zu einer Verschlechterung der Note. Wenn wir eine gewöhnliche Pearson-Korrelation berechnen, zeigt sich eine starke Beziehung zwischen dem Arbeitseinsatz und der Note, mit einem Korrelationskoeffizienten von 0,91. Dies entspricht jedoch nicht der Beobachtung, dass eine Erhöhung der geleisteten Arbeitsstunden immer zu einer Verbesserung der Note führt. In gewissem Sinne möchten wir sagen können, dass die Korrelation perfekt ist, aber wir haben eine etwas andere Vorstellung davon, was eine „Beziehung“ ist. Was wir suchen, ist etwas, das die Tatsache festhält, dass es hier eine perfekte ordinale Beziehung gibt. Das heißt, wenn Student 1 mehr Stunden arbeitet als Student 2, dann können wir garantieren, dass Student 1 die bessere Note erhält. Das sagt eine Korrelation von r = 0,91 aber überhaupt nicht aus.
Abb. 112 Die Beziehung zwischen den geleisteten Arbeitsstunden und der erhaltenen Note für einen fiktiven Datensatz mit 10 Studenten (jeder Kreis entspricht einem Studenten). Die gestrichelte Linie in der Mitte zeigt die lineare Beziehung zwischen den beiden Variablen mit einer starken Pearson-Korrelation von r = 0,91. Interessant ist jedoch, dass es tatsächlich eine perfekte monotone Beziehung zwischen den beiden Variablen gibt. Wie die durchgezogene Linie zeigt, steigt in diesem Beispiel mit zunehmender Zahl der geleisteten Arbeitsstunden immer auch die erhaltene Note. Dies spiegelt sich in einer Spearman-Korrelation von ρ = 1,00 wider. Bei einem so kleinen Datensatz ist es jedoch eine offene Frage, welche der Korrelationen die tatsächliche Beziehung besser beschreibt.
Wie sollten wir das angehen? Eigentlich ist es ganz einfach. Wenn wir nach ordinalen Beziehungen suchen, müssen wir die Daten nur so behandeln, als wären sie ordinalskaliert ! Anstatt also den Arbeitseinsatz in Form von „Arbeitsstunden“ zu messen, sollten wir alle 10 Studenten entsprechend der Rangfolge ihrer Arbeitsstunden einordnen. Das heißt, Student 1 hat von allen am wenigsten gearbeitet (2 Stunden) und erhält daher den niedrigsten Rang (Rang = 1). Student 4 war etwas fleißiger, hat aber während des gesamten Semesters nur 6 Stunden Arbeit geleistet, und erhält daher den nächsthöheren Rang (Rang = 2). Beachten Sie, dass ich „Rang = 1“ im Sinne von „niedriger Rang“ verwende. In der Alltagssprache sprechen wir manchmal von „Rang = 1“, um den „höchsten Rang“ und nicht den „niedrigsten Rang“ zu meinen. Seien Sie also vorsichtig, Sie können eine Rangfolge „vom kleinsten Wert zum größten Wert“ (d. h. klein ist gleich Rang 1) oder „vom größten Wert zum kleinsten Wert“ (d. h. groß ist gleich Rang 1) erstellen. In diesem Fall rangiere ich vom kleinsten zum größten Wert, aber da man sehr leicht vergessen kann, wie man die Rangfolge einstellt, muss man sich schon ein wenig Mühe geben, sich daran zu erinnern!
Schauen wir uns also unsere Studenten an, wenn wir sie in Bezug auf Aufwand und Belohnung von der schlechtesten bis zur besten Leistung einstufen:
Rang (geleistete Arbeitsstunden) |
Rang (erhaltene Note) |
|
|---|---|---|
Student 1 |
1 |
1 |
Student 2 |
10 |
10 |
Student 3 |
6 |
6 |
Student 4 |
2 |
2 |
Student 5 |
3 |
3 |
Student 6 |
5 |
5 |
Student 7 |
4 |
4 |
Student 8 |
8 |
8 |
Student 9 |
7 |
7 |
Student 10 |
9 |
9 |
Die Ränge sind identisch. Der Student, der sich am meisten angestrengt hat, hat die beste Note bekommen, der Student mit der geringsten Anstrengung hat die schlechteste Note bekommen usw. Wie die obige Tabelle zeigt, sind die Ränge jeweils identisch. Wenn wir sie nun zueinander in Beziehung setzen, erhalten wir eine perfekte Beziehung, mit einer Korrelation von 1,0.
Was wir soeben neu erfunden haben, ist Spearmans Rangfolgekorrelation, die üblicherweise als ρ bezeichnet wird, um sie von der Pearson-Korrelation r zu unterscheiden. Wir können Spearmans ρ mit jamovi berechnen, indem wir einfach die Checkbox Spearman innerhalb der Optionen von Correlation Matrix aktivieren.