Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft
Schätzen eines linearen Regressionsmodells
Abb. 117 Darstellung der Residuen mit der am besten passenden Regressionsgerade (links) und einer schlechten Regressionsgerade (rechts). Die Residuen sind bei der guten Regressionsgerade viel kleiner. Auch hier ist dies keine Überraschung, da die gute Linie genau durch die Mitte der Daten verläuft.
Jetzt erstellen wir unsere Diagramme noch einmal, aber dieses Mal füge ich einige Linien hinzu, um die Größe der Residuen für alle Beobachtungen zu zeigen. Wenn die Regressionsgerade gut gewählt ist, sehen unsere Residuen (die Längen der durchgezogenen schwarzen Linien) alle ziemlich klein aus, wie in Abb. 117 (links) zu sehen ist, aber wenn die Regressionsgerade schlecht gewählt ist, sind die Residuen viel größer, wie man in Abb. 117 (rechts) sehen kann. Vielleicht ist das, was wir in einem Regressionsmodell „wollen“, kleine Residuen. Ja, das scheint wirklich Sinn zu machen. Ich würde sogar so weit gehen zu sagen, dass die am besten passende Regressionsgerade diejenige ist, welche die kleinsten Residuen aufweist. Oder, noch besser, da Statistiker anscheinend gerne Quadrate von allem nehmen, warum sollte man das nicht sagen: Die geschätzten Regressionskoeffizienten, \(\hat{b}_0\) und \(\hat{b}_1\), sind diejenigen, die die Summe der quadrierten Residuen minimieren. Wir könnten das entweder schreiben als
oder als
Das klingt sogar noch besser. Und da ich es so eingerückt habe, bedeutet das wahrscheinlich, dass dies die richtige Antwort ist. Und da dies die richtige Antwort ist, lohnt es sich wahrscheinlich, die Tatsache zu erwähnen, dass unsere Regressionskoeffizienten Schätzungen sind (wir versuchen, die Parameter zu schätzen, die eine Population beschreiben!). Deshalb habe ich die kleinen Hüte hinzugefügt, so dass wir \(\hat{b}_0\) und \(\hat{b}_1\) erhalten, anstatt b0 und b1. Abschließend sollte ich noch anmerken, dass es mehr als eine Möglichkeit gibt, ein Regressionsmodell zu schätzen. Der technischere Name für dieses Schätzverfahren ist ordinary least squares (OLS) regression (Kleinstquadrate-Kriterium oder Minimieren der quadrierten Abweichungen).
An diesem Punkt haben wir nun eine konkrete Definition dafür, was als unsere „beste“ Wahl von Regressionskoeffizienten gilt, \(\hat{b}_0\) und \(\hat{b}_1\). Wenn unsere optimalen Regressionskoeffizienten diejenigen sind, die die Summe der quadrierten Residuen minimieren, dann stellt sich natürlich die Frage, wie wir diese wunderbaren Zahlen finden. Die eigentliche Antwort auf diese Frage ist kompliziert und hilft Ihnen nicht, um die Logik der Regression zu verstehen.[1] Daher verwenden wir gleich jamovi, um die ganze schwere Arbeit zu erledigen, anstatt Ihnen zuerst den langen, mühsamen und schrittweisen Weg zu zeigen und dann die wunderbare Abkürzung zu „enthüllen“, die jamovi bietet.
Lineare Regression in jamovi
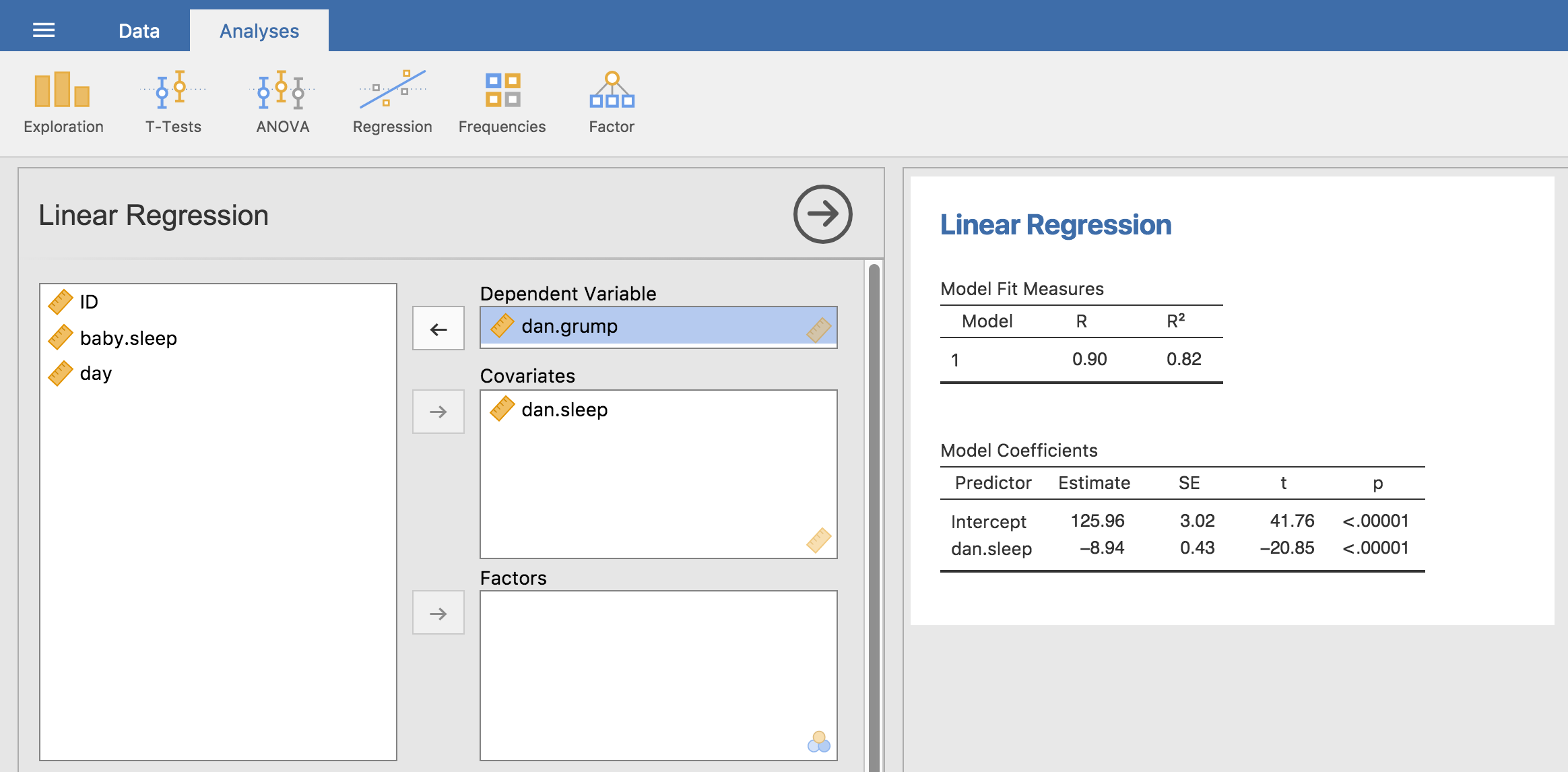
Abb. 118 jamovi-Screenshot mit einer einfachen linearen Regressionsanalyse
Um eine lineare Regression unter Verwendung des Datensatzes parenthood durchzuführen, öffnen Sie die Analyse Regression - Linear Regression in jamovi. Verschieben Sie dann dani.grump in die Dependent Variable und dani.sleep in das Variablenfeld Covariates. Dadurch ergeben sich die in Abb. 118 gezeigten Ergebnisse, mit einem Interzept \(\hat{b}_0\) = 125,96 und einer Steigung \(\hat{b}_1\) = -8,94. Mit anderen Worten, die am besten passende Regressionsgerade, die ich in Abb. 116 eingezeichnet habe, hat die folgende Formel:
Interpretation des geschätzten Modells
Das Wichtigste, was man verstehen muss, ist, wie man diese Koeffizienten interpretieren kann. Beginnen wir mit \(\hat{b}_1\), der Steigung. Wenn wir uns an die Definition der Steigung erinnern, bedeutet ein Regressionskoeffizient von \(\hat{b}_1\) = -8,94, dass, wenn ich Xi um 1 erhöhe, ich Yi um 8,94 vermindern werde. Das heißt, dass jede zusätzliche Stunde Schlaf, die ich gewinne, meine Stimmung verbessert und meine schlechte Laune um 8,94 Punkte verringert. Was ist mit dem Schnittpunkt? Nun, da \(\hat{b}_0\) dem „erwarteten Wert von Yi entspricht, wenn Xi gleich 0 ist“, ist das ziemlich einfach. Das bedeutet, dass, wenn ich null Stunden Schlaf bekomme (Xi = 0), meine schlechte Laune einen unglaublich hohen Wert erreichen wird (Yi = 125,96). Das sollte man besser vermeiden, denke ich.