Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft
Durchführen von Hypothesentests für Regressionsmodelle
Bisher haben wir darüber gesprochen, was ein Regressionsmodell ist, wie die Koeffizienten eines Regressionsmodells geschätzt werden und wie wir die Leistung des Modells quantifizieren (der letzte Punkt ist übrigens unser Maß für die Effektstärke). Der nächste Punkt, über den wir sprechen müssen, sind Hypothesentests. Es gibt zwei verschiedene (aber verwandte) Arten von Hypothesentests, über die wir sprechen müssen: solche, bei denen wir testen, ob das Regressionsmodell insgesamt signifikant besser abschneidet als ein Nullmodell, und solche, bei denen wir testen, ob ein bestimmter Regressionskoeffizient sich signifikant von Null unterscheidet.
Testen des gesamten Modells
Nehmen wir an, Sie haben Ihr Regressionsmodell geschätzt. Der erste Hypothesentest, den Sie versuchen könnten, ist die Nullhypothese, dass es keine Beziehung zwischen den Prädiktoren und dem Ergebnis gibt, und die Alternativhypothese, dass die Daten genau so verteilt sind, wie es das Regressionsmodell vorhersagt.
Formal entspricht unser „Nullmodell“ dem recht trivialen „Regressionsmodell“, bei dem wir keine Prädiktoren und nur den Interzept-Term b0 einbeziehen:
Unser „Alternativmodell“ wird mit der üblichen Formel für ein multiples Regressionsmodell mit K Prädiktoren beschrieben:
Wie können wir diese beiden Hypothesen gegeneinander testen? Der Trick besteht darin, zu verstehen, dass es möglich ist, die totale Quadratsumme SStot in die Quadratsumme der Residuen SSres und die durch das Regressionsmodell erklärte Quadratsumme SSmod aufzuteilen (und da die Quadratsumme nichts anderes ist als die Varianz multipliziert mit N bzw. N - 1 hätte ich genauso gut Varianz an Stelle von Quadratsumme schreiben können). Ich überspringe die technischen Details, da wir dazu später kommen, wenn wir uns die ANOVA in Kapitel Vergleich mehrerer Mittelwerte (einfaktorielle ANOVA) ansehen. Aber beachten Sie einfach, dass
Und wir können die Quadratsummen in mittlere quadrierte Abweichungen umwandeln, indem wir sie durch die Freiheitsgrade teilen.
Wie viele Freiheitsgrade haben wir also? Wie zu erwarten, ist der df des Modells eng mit der Anzahl der Prädiktoren verbunden, die wir einbezogen haben. Tatsächlich stellt sich heraus, dass dfmod = K. Für die Residuen sind die gesamten Freiheitsgrade dfres = N - K - 1.
Da wir nun unsere mittleren Quadratwerte haben, können wir eine F-Statistik wie folgt berechnen
und die damit verbundenen Freiheitsgrade sind K und N - K - 1.
Wir werden mehr über die F-Statistik in Kapitel Vergleich mehrerer Mittelwerte (einfaktorielle ANOVA) erfahren, aber für den Moment reicht es, wenn wir wissen, dass wir große F-Werte als Hinweis darauf interpretieren können, dass die Nullhypothese im Vergleich zur Alternativhypothese schlecht abschneidet. In Kürze werde ich Ihnen zeigen, wie Sie den Test in jamovi auf einfache Weise durchführen können, aber sehen wir uns zunächst die Tests für die einzelnen Regressionskoeffizienten an.
Tests für einzelne Koeffizienten
Der F-Test, den wir gerade eingeführt haben, ist nützlich, um zu überprüfen, ob das Modell als Ganzes besser als der Zufall funktioniert. Wenn Ihr Regressionsmodell kein signifikantes Ergebnis für den F-Test liefert, dann haben Sie wahrscheinlich kein sehr gutes Regressionsmodell (oder Sie haben wahrscheinlich eher keine sehr guten Daten). Das Nichtbestehen dieses Tests ist zwar ein ziemlich starker Indikator dafür, dass das Modell Probleme hat, aber das Bestehen des Tests (d. h. die Zurückweisung der Nullhypothese bzw. des Nullmodells) bedeutet nicht zwanghsläufig, dass das Modell gut ist! Sie fragen Sie sich vielleicht, warum das so ist? Die Antwort darauf finden Sie, wenn Sie sich die Koeffizienten des multiplen Regressionsmodells ansehen, das wir bereits unter Tab. 15 im Abschnitt Multiple lineare Regression betrachtet haben, wo die Koeffizienten 125,966 (für das Interzept), -8,950 (für dani.sleep) und 0,011 (für baby.sleep) betragen. Es fällt auf, dass der geschätzte Regressionskoeffizient für die Variable baby.sleep winzig ist, im Vergleich zu dem Wert, den wir für dani.sleep erhalten. Ich finde dies besonders aufschlussreich, in Anbetracht der Tatsache, dass diese beiden Variablen absolut auf der gleichen Skala liegen (sie werden beide als „geschlafene Stunden“ gemessen). In der Tat beginne ich zu vermuten, dass es wirklich nur auf die Menge an Schlaf ankommt, die ich bekomme, wenn es darum geht, meine schlechte Laune vorherzusagen.
Wir können einen Hypothesentest wiederverwenden, den wir bereits besprochen haben, den t-Test. Der Test, an dem wir interessiert sind, hat die Nullhypothese, dass der wahre Regressionskoeffizient Null ist (b = 0), die gegen die Alternativhypothese, dass er es nicht ist (b ≠ 0), getestet werden soll. Das heißt:
Wie können wir das testen? Wenn der zentrale Grenzwertsatz uns wohlgesonnen ist, können wir vermuten, dass die Stichprobenverteilung von \(\hat{b}\), dem geschätzten Regressionskoeffizienten, eine Normalverteilung mit einem Mittelwert ist, der auf b zentriert ist. Das würde bedeuten, wenn die Nullhypothese wahr wäre, hätte die Stichprobenverteilung von \(\hat{b}\) einen Mittelwert von Null und eine unbekannte Standardabweichung. Wenn wir einen guten Schätzwert für den Standardfehler des Regressionskoeffizienten \(SE(\hat{b})\) finden können, dann können wir die Hypothese testen. Das ist genau die Situation, für die wir in Kapitel Vergleich zweier Mittelwerte den t-Test bei einer Stichprobe eingeführt haben. Definieren wir also eine t-Statistik wie folgt:
Ich überspringe die Gründe dafür, aber unsere Freiheitsgrade sind in diesem Fall df = N - K - 1. Irritierenderweise ist die Schätzung des Standardfehlers des Regressionskoeffizienten, \(SE(\hat{b})\), nicht so einfach zu berechnen wie der Standardfehler des Mittelwertes, den wir für die einfacheren t-Tests in Kapitel Vergleich zweier Mittelwerte verwendet haben. Tatsächlich ist die Formel etwas hässlich und nicht sehr hilfreich.[1] Für unsere Zwecke reicht es aus, darauf hinzuweisen, dass der Standardfehler des geschätzten Regressionskoeffizienten sowohl von den Prädiktor- als auch von der Ergebnisvariablen abhängt und empfindlich auf Verletzungen der Annahme der Varianzhomogenität reagiert (die in Kürze besprochen wird).
In jedem Fall kann diese t-Statistik auf die gleiche Weise interpretiert werden wie die t-Statistik, die wir in Kapitel Vergleich zweier Mittelwerte besprochen haben. Angenommen, Sie haben eine zweiseitige Alternative (d.h. es ist Ihnen egal, ob b > 0 oder b < 0), dann sind es hohe (Absolut-)Werte von t (d.h. hohe Werte mit entweder negativem oder ohne, d.h. positivem, Vorzeichen), die darauf hindeuten, dass Sie die Nullhypothese ablehnen können.
Durchführen der Hypothesentests in jamovi
Um alle Statistiken zu berechnen, über die wir bisher gesprochen haben, müssen Sie lediglich sicherstellen, dass alle relevanten Optionen in jamovi gesetzt sind, und dann die Regression ausführen. Wenn wir das tun, wie in Abb. 120 gezeigt, erhalten wir eine ganze Reihe nützlicher Ausgaben.
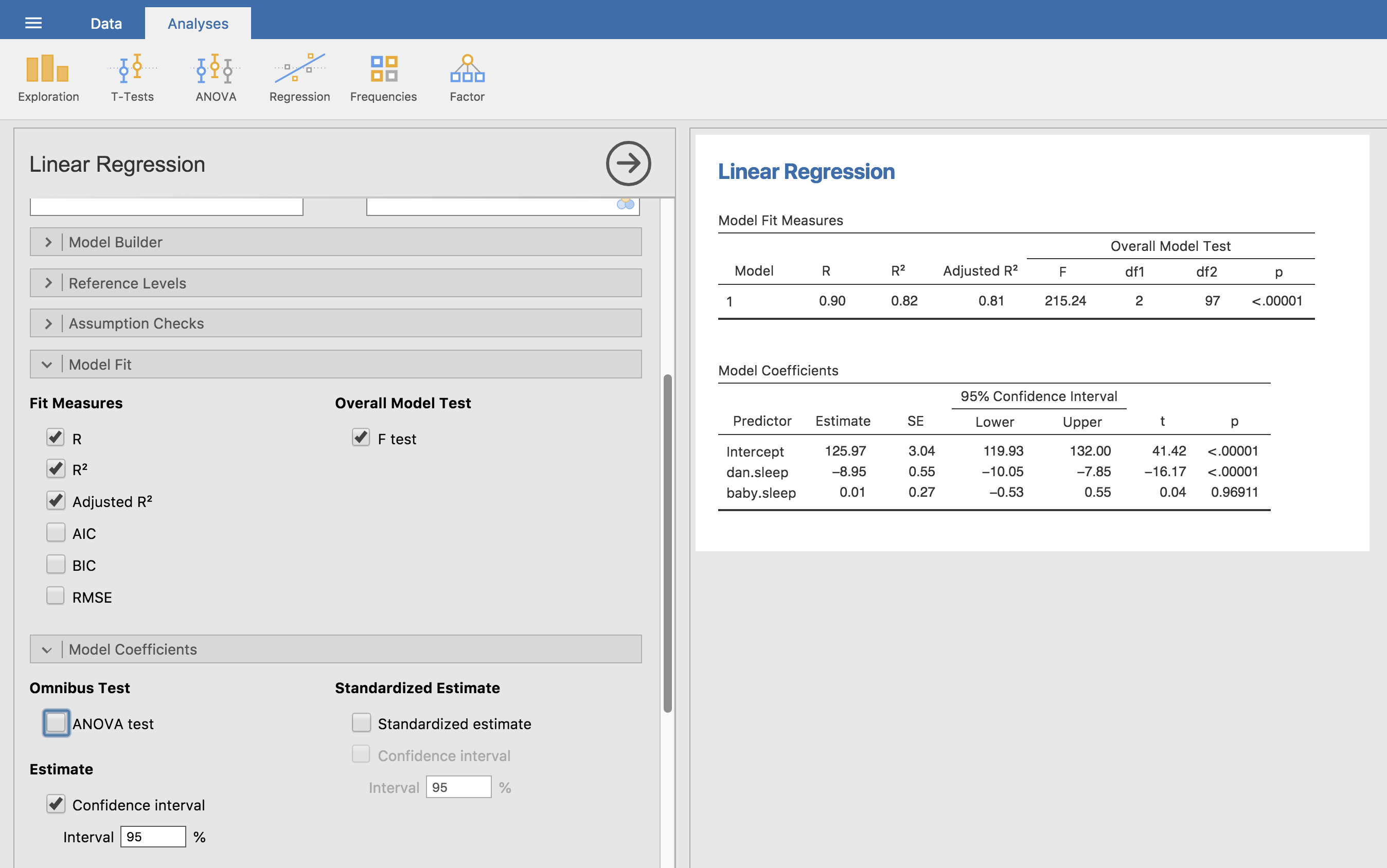
Abb. 120 jamovi-Screenshot, der eine multiple lineare Regressionsanalyse zeigt, bei der einige wichtige Ausgabeoptionen gesetzt wurden.
Die Model Coefficients am Ende der jamovi-Analyseergebnisse, die in Abb. 120 dargestellt sind, enthält die Koeffizienten des Regressionsmodells. Jede Zeile in dieser Tabelle bezieht sich auf einen der Koeffizienten des Regressionsmodells. Die erste Zeile ist der Interzept-Term, und die weiteren Zeilen befassen sich mit den einzelnen Prädiktoren. Die Spalten geben Ihnen alle relevanten Informationen. Die erste Spalte ist die aktuelle Schätzung von b (z. B. 125,97 für das Interzept und -8,95 für den Prädiktor dani.sleep). Die zweite Spalte ist die Schätzung des Standardfehlers :math:hatsigma_b`. Die dritte und vierte Spalte enthalten die unteren und oberen Werte für das 95%-Konfidenzintervall um die Schätzung von b (mehr dazu später). Die fünfte Spalte enthält die t-Statistik, und es ist erwähnenswert, dass dieser Wert in dieser Tabelle immer \(t= \hat{b}/ SE(\hat{b})\) ist. In der letzten Spalte schließlich finden Sie den p-Wert für jeden dieser Tests.[2]
Das Einzige, was in der Koeffiziententabelle nicht aufgeführt ist, sind die Freiheitsgrade, die im t-Test verwendet werden. Diese sind immer N - K - 1 ist und in der Tabelle mit Model Fit Measures weiter oben in der Ausgabe aufgeführt. Aus dieser Tabelle geht hervor, dass das Modell signifikant besser abschneidet, als man zufällig erwarten würde (F(2,97) = 215.24, p < 0.001), was nicht allzu überraschend ist: der R² = 0.81 Wert zeigt an, dass das Regressionsmodell 81 % der Variabilität der Ergebnisgröße erklärt (und 82 % für das bereinigte R²). Wenn wir uns jedoch die t-Tests für jeden der einzelnen Koeffizienten ansehen, haben wir deutliche Hinweise darauf, dass die Variable baby.sleep keinen signifikanten Effekt hat. Die gesamte Arbeit in diesem Modell wird von der Variable dani.sleep erledigt. Zusammengenommen deuten diese Ergebnisse darauf hin, dass dieses Regressionsmodell eigentlich das falsche Modell für die Daten ist. Es wäre wahrscheinlich besser, den Prädiktor baby.sleep ganz wegzulassen. Mit anderen Worten: Das einfache Regressionsmodell, mit dem wir begonnen haben, ist das bessere Modell.