Autor des Abschnitts: Danielle J. Navarro and David R. Foxcroft

Maße der Variabilität

Die Statistiken, die wir bisher besprochen haben, beziehen sich alle auf die zentrale Tendenz. Das heißt, sie alle sagen aus, welche Werte in den Daten „in der Mitte“ liegen oder „beliebt“ sind. Die zentrale Tendenz ist jedoch nicht die einzige Art der zusammenfassenden Statistik, die wir berechnen wollen. Der zweite Aspekt, der uns interessiert, ist ein Maß für die Variabilität der Daten. Das heißt, wie „gestreut“ sind die Daten? Wie „weit“ entfernt vom Mittelwert oder Median liegen die beobachteten Werte tendenziell? Nehmen wir zunächst an, dass es sich bei den Daten um eine Intervall- oder Verhältnisskala handelt. Wir verwenden weiterhin die afl.margins-Variable. Anhand dieser Daten werden wir verschiedene Streuungsmaße erörtern, die jeweils unterschiedliche Stärken und Schwächen aufweisen.

Spannweite (range)

Der Wertebereich einer Variablen ist einfach beschrieben. Es handelt sich um den größten Wert, minus den kleinsten Wert. Für die Variable ist der Maximalwert 116 und der Minimalwert 0. Obwohl der Wertebereich die einfachste Art ist, um „Variabilität“ zu quantifizieren, ist er auch eine der schlechtesten. Aus unserer Diskussion über den Mittelwert wissen wir, dass unser zusammenfassendes Maß robust sein soll. Wenn der Datensatz einen oder zwei extreme Werte enthält, möchten wir, dass unsere Statistik durch diese Fälle nicht übermäßig beeinflusst wird. Zum Beispiel durch eine Variable mit sehr extremen Werten (Ausreißern)

-100, 2, 3, 4, 5, 6, 7, 8, 9, 10

wird klar, dass der Wertebereich nicht stabil ist. Diese Variable hat einen Bereich von 110, aber wenn der Ausreißer entfernt würde, hätten wir einen Bereich von nur 8.

Interquartilsabstand

Der Interquartilabstand (IQR) ist wie der Bereich, aber anstelle der Differenz zwischen dem größten und dem kleinsten Wert wird die Differenz zwischen dem 25. Falls Sie noch nicht wissen, was ein Perzentil ist: Das 10. Perzentil eines Datensatzes ist die kleinste Zahl x, bei der 10 % der Daten kleiner sind als x. Die Idee ist uns bereits begegnet. Der Median eines Datensatzes ist sein 50. Perzentil! In jamovi können Sie ganz einfach das 25., 50. und 75. Perzentil angeben, indem Sie die Checkbox Quartiles``unter ``Exploration → Descriptives → Statistics aktivieren.

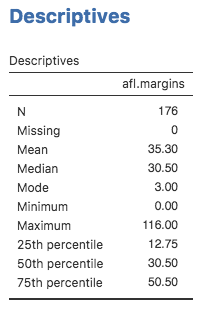
Abb. 12 jamovi-Screenshot mit den Quartilen der Variable afl.margins

Es überrascht nicht, dass das 50. Perzentil in Abb. 12 dem Medianwert entspricht. Wenn man bedenkt, dass 50,50 - 12,75 = 37,75 ist, kann man sehen, dass der Interquartilabstand für die AFL-Gewinnspannen 2010 37,75 beträgt. Während es offensichtlich ist, wie die Spannweite zu interpretieren ist, ist es etwas weniger offensichtlich, wie man den IQR interpretiert. Der einfachste Weg, sich das vorzustellen, ist folgender: Der Interquartilabstand ist der Bereich, der von der „mittleren Hälfte“ der Daten abgedeckt wird. Das heißt, ein Viertel der Daten liegt unter dem 25. Perzentil und ein Viertel der Daten über dem 75. Perzentil, so dass die „mittlere Hälfte“ der Daten dazwischen liegt. Und der IQR ist der Bereich, der von dieser mittleren Hälfte abgedeckt wird.

Mittlere absolute Abweichung

Die beiden Maße, die wir bisher betrachtet haben, die Spannweite und der Interquartilabstand, beruhen beide auf der Idee, dass wir die Streuung der Daten messen können, indem wir uns die Perzentile der Daten ansehen. Dies ist jedoch nicht die einzige Möglichkeit, das Problem zu betrachten. Ein anderer Ansatz besteht darin, einen aussagekräftigen Bezugspunkt zu wählen (in der Regel den Mittelwert oder den Median) und dann die „typischen“ Abweichungen von diesem Bezugspunkt anzugeben. Was verstehen wir unter „typischer“ Abweichung? In der Regel ist dies der Mittelwert oder der Medianwert dieser Abweichungen. In der Praxis führt dies zu zwei verschiedenen Maßen: die „mittlere absolute Abweichung“ (vom Mittelwert) und die „mittlere absolute Abweichung“ (vom Median). Nach dem, was ich gelesen habe, scheint das auf dem Median basierende Maß in der Statistik verwendet zu werden und auch das bessere von beiden zu sein. Um ehrlich zu sein, glaube ich aber nicht, dass es in der Psychologie häufig verwendet wird. Das auf dem Mittelwert basierende Maß taucht jedoch gelegentlich in der Psychologie auf. In diesem Abschnitt werde ich über das erste Maß sprechen, auf das zweite komme ich später zurück.

Da der vorige Absatz etwas abstrakt geklungen haben mag, wollen wir die mittlere absolute Abweichung vom Mittelwert schrittweise durchgehen. Das Nützliche an dieser Kennzahl ist, dass der Name genau angibt, wie sie zu berechnen ist. Betrachten wir unsere AFL-Gewinnspannen-Daten und nehmen wir wieder einmal an, dass es insgesamt nur 5 Spiele mit Gewinnspannen von 56, 31, 56, 8 und 32 gibt. Da unsere Berechnungen auf einer Untersuchung der Abweichung von einem Bezugspunkt (in diesem Fall dem Mittelwert) beruhen, müssen wir zunächst den Mittelwert X̄ berechnen. Für diese fünf Beobachtungen beträgt unser Mittelwert X̄ = 36,6. Der nächste Schritt besteht darin, jede unserer Beobachtungen X_i in einen Abweichungswert umzuwandeln. Dazu berechnen wir die Differenz zwischen der Beobachtung X_i und dem Mittelwert X̄. Das heißt, der Abweichungswert ist definiert als X_i - X̄. Für die erste Beobachtung in unserer Stichprobe ist dies gleich 56 - 36,6 = 19,4. Okay, das ist einfach genug. Der nächste Schritt besteht darin, diese Abweichungen in absolute Abweichungen umzuwandeln, und zwar indem wir alle negativen Werte in positive umwandeln. Mathematisch gesehen würden wir den absoluten Wert von -3 als |-3| bezeichnen, und so sagen wir, dass |-3| = 3`. Wir verwenden hier den absoluten Wert, weil es uns nicht wirklich interessiert, ob der Wert höher oder niedriger als der Mittelwert ist, sondern nur, wie nah er am Mittelwert liegt. Um diesen Vorgang so deutlich wie möglich zu machen, zeigt die folgende Tabelle diese Berechnungen für alle fünf Beobachtungen:

Beschreibung:	welches Spiel	Wert	Abweichung vom Mittelwert	absolute Differenz
Notation:	i	Xi	Xi - X̄	| Xi - X̄ |
	1	56	19.4	19.4
	2	31	-5.6	5.6
	3	56	19.4	19.4
	4	8	-28.6	28.6
	5	32	-4.6	4.6

Nachdem wir nun für jede Beobachtung im Datensatz den absoluten Abweichungswert berechnet haben, müssen wir nur noch den Mittelwert dieser Werte berechnen. Lassen Sie uns das tun:

\[\frac{19.4 + 5.6 + 19.4 + 28.6 + 4.6}{5} = 15.52\]

Und schon sind wir fertig. Die mittlere absolute Abweichung für diese fünf Ergebnisse beträgt 15,52 Punkte.

Aber auch wenn unsere Berechnungen für dieses kleine Beispiel abgeschlossen sind, müssen wir noch über einige Dinge sprechen. Zunächst sollten wir wirklich versuchen, eine richtige mathematische Formel aufzuschreiben. Dazu brauche ich aber eine mathematische Notation für die mittlere absolute Abweichung. Irritierenderweise haben die „mittlere absolute Abweichung (vom Mittelwert)“ und die „mittlere absolute Abweichung (vom Median)“ die gleiche Bezeichnung und das gleiche Akronym (MAD in Englisch), was zu einer gewissen Mehrdeutigkeit führt, so dass ich mir besser etwas anderes für die mittlere absolute Abweichung vom Mittelwert ausdenken sollte. Ich werde stattdessen AAD verwenden, kurz für „average absolute deviation“. Da wir nun eine eindeutige Notation haben, hier die Formel, die beschreibt, was wir gerade berechnet haben:

\[AAD(X) = \frac{1}{N} \sum_{i = 1}^N |X_i - \bar{X}|\]

Varianz

Das Maß der durchschnittlichen absoluten Abweichung hat zwar seine Berechtigung, ist aber nicht das beste Maß für die Variabilität, das man verwenden kann. Aus rein mathematischer Sicht gibt es einige gute Gründe, quadrierte Abweichungen den absoluten Abweichungen vorzuziehen. Wenn wir das tun, erhalten wir ein Maß, das Varianz genannt wird, das eine Menge wirklich netter statistischer Eigenschaften hat, die ich für’s Erste ignorieren werde.[1] Sie hat gleichzeitig einen massiven psychologischen Makel, aus dem ich gleich eine große Sache machen werde. Die Varianz eines Datensatzes X wird manchmal als Var(X) geschrieben, aber üblicherweise wird sie als s² bezeichnet (der Grund dafür wird in Kürze klarer werden).

Die Formel, mit der wir die Varianz einer Reihe von Beobachtungen berechnen, lautet wie folgt:

\[\mbox{Var}(X) = \frac{1}{N} \sum_{i=1}^N \left( X_i - \bar{X} \right)^2\]

Wie Sie sehen, handelt es sich im Grunde um dieselbe Formel, die wir zur Berechnung der durchschnittlichen absoluten Abweichung verwendet haben, nur dass wir an Stelle von „absoluten Abweichungen“ die „quadrierten Abweichungen“ verwenden. Aus diesem Grund wird die Varianz manchmal auch als „mittlere quadrierte Abweichung“ bezeichnet.

Nachdem wir nun die Grundidee verstanden haben, wollen wir uns ein konkretes Beispiel ansehen. Nehmen wir wieder die ersten fünf AFL-Spiele als Datengrundlage. Wenn wir den gleichen Ansatz wie beim letzten Mal verfolgen, erhalten wir die folgende Tabelle:

Beschreibung:	welches Spiel	Wert	Abweichung vom Mittelwert	quadrierte Abweichung
Notation:	i	Xi	Xi - X̄	(Xi - X̄)²
	1	56	19.4	376.36
	2	31	-5.6	31.36
	3	56	19.4	376.36
	4	8	-28.6	817.96
	5	32	-4.6	21.16

Diese letzte Spalte enthält alle unsere quadrierten Abweichungen, so dass wir nur noch den Mittelwert bilden müssen. Wenn wir das von Hand, d.h. mit einem Taschenrechner, machen, erhalten wir eine Varianz von 324,64. Aufregend, nicht wahr? Lassen wir die brennende Frage, die ihr euch wahrscheinlich alle stellt (nämlich: Was zum Teufel bedeutet eine Varianz von 324,64?), erst einmal beiseite und gehen stattdessen etwas genauer darauf ein, wie man die Berechnungen in jamovi durchführt, denn dabei kommt etwas sehr Merkwürdiges zum Vorschein. Starten Sie eine neue jamovi-Sitzung, indem Sie auf die Hauptmenü-Schaltfläche (☰; in der oberen linken Ecke) klicken und New wählen. Geben Sie nun die ersten fünf Werte aus der aflsmall_margins-Datendatei in Spalte A ein (56, 31, 56, 8, 32). Ändern Sie den Variablentyp in Continuous und setzen Sie die Checkbox Variance unter Descriptives, und Sie erhalten die gleichen Werte für die Varianz wie die, welche wir von Hand berechnet haben (324.64). Nein, warten Sie, Sie erhalten eine völlig andere Antwort (405.80) - siehe Abb. 13. Das ist einfach seltsam. Ist jamovi kaputt? Ist das ein Tippfehler? Bin ich ein Idiot?

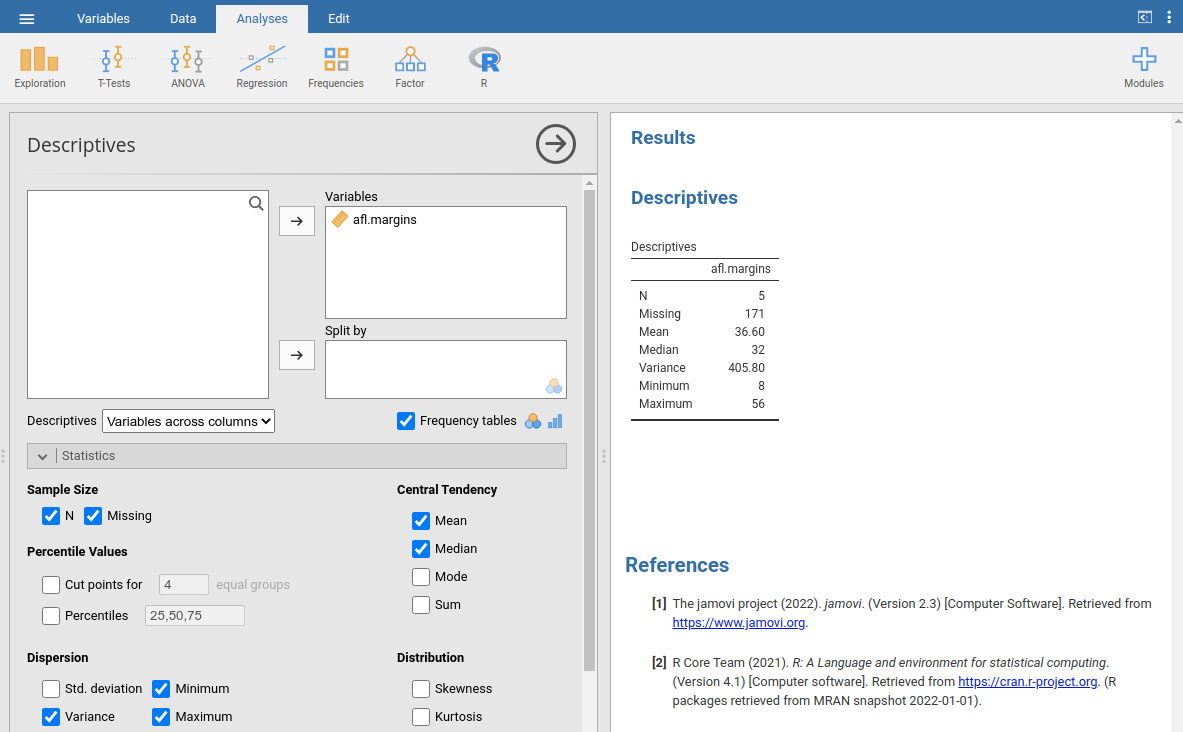
Abb. 13 jamovi-Screenshot mit der Varianz für die ersten 5 Werte der Variablen afl.margins

Die Antwort lautet: Nein.[2] Es ist kein Tippfehler, und auch jamovi macht keinen Fehler. Tatsächlich ist es sehr einfach zu erklären, was jamovi hier tut, aber etwas schwieriger zu erklären, warum jamovi es tut. Beginnen wir also mit dem „Was“. Was jamovi tut, ist die Auswertung einer etwas anderen Formel als der, die ich Ihnen oben gezeigt habe. Anstatt den Mittelwert der quadrierten Abweichungen zu bilden, wofür man durch die Anzahl der Datenpunkte N dividieren muss, hat sich jamovi dafür entschieden, durch N - 1 zu dividieren.

Mit anderen Worten, die Formel, die jamovi verwendet, ist diese:

\[\frac{1}{N - 1} \sum_{i=1}^N \left( X_i - \bar{X} \right)^2\]

Das ist also das was. Die eigentliche Frage ist, warum jamovi durch N - 1 und nicht durch N dividiert. Schließlich soll die Varianz die mittlere quadrierte Abweichung sein, richtig? Sollten wir also nicht durch N, die tatsächliche Anzahl der Beobachtungen in der Stichprobe, dividieren? Nun, ja, das sollten wir. Wie wir jedoch in Kapitel Schätzen unbekannter Größen anhand einer Stichprobe erörtern, gibt es einen feinen Unterschied zwischen der „Beschreibung einer Stichprobe“ und dem „Erstellen von Vermutungen über die Grundgesamtheit, aus der die Stichprobe stammt“. Bis zu diesem Punkt war es in Unterschied ohne Unterschied. Unabhängig davon, ob man eine Stichprobe beschreibt oder Rückschlüsse auf die Grundgesamtheit zieht, wird der Mittelwert auf genau dieselbe Weise berechnet. Das gilt aber nicht für die Varianz, die Standardabweichung oder viele andere Maße. Bei dem, was ich Ihnen anfangs erklärt habe (d. h. den tatsächlichen Mittelwert nehmen und durch N teilen), wird davon ausgegangen, dass Sie buchstäblich beabsichtigen, die Varianz der Stichprobe zu berechnen. In den meisten Fällen sind Sie jedoch nicht sonderlich an der Stichprobe an sich interessiert. Die Stichprobe dient vielmehr dazu, Ihnen etwas über die Welt zu sagen. Wenn dies der Fall ist, bewegen Sie sich weg von der Berechnung einer „Stichprobenstatistik“ und hin zur Schätzung eines „Populationsparameters“. Aber ich greife mir selbst vor. Für den Moment wollen wir einfach darauf vertrauen, dass jamovi weiß, was es tut, und wir werden die Frage später wieder aufgreifen, wenn wir über das Schätzen sprechen.

Okay, eine letzte Sache. Dieser Abschnitt hat sich bisher ein bisschen wie ein Krimi gelesen. Ich habe Ihnen gezeigt, wie man die Varianz berechnet, ich habe die seltsame „N - 1“-Sache beschrieben, die jamovi macht, und ich habe angedeutet, warum sie da ist, aber ich habe die wichtigste Sache nicht erwähnt. Wie interpretieren Sie die Varianz? Deskriptive Statistiken sollen ja schließlich Dinge beschreiben, und im Moment ist die Varianz nur eine Kauderwelsch-Zahl. Der Grund, warum ich Ihnen keine menschenfreundliche Interpretation der Varianz gegeben habe, ist leider, dass es keine gibt. Dies ist das größte Problem mit der Varianz. Obwohl sie einige elegante mathematische Eigenschaften hat, die darauf hindeuten, dass sie wirklich eine fundamentale Größe zur Beschreibung von Variation ist, ist sie völlig nutzlos, wenn man mit einem Menschen kommunizieren will. Die Varianz ist in Bezug auf die ursprüngliche Variable völlig uninterpretierbar! Alle Zahlen wurden quadriert und haben keine Bedeutung mehr. Das ist ein großes Problem. Laut der Tabelle, die ich vorhin vorgestellt habe, war zum Beispiel die Marge in Spiel 1 „376,36 Punkte zum Quadrat höher als die durchschnittliche Marge“. Das ist genau so dumm, wie es klingt, und wenn wir eine Varianz von 324,64 berechnen, sind wir in der gleichen Situation. Ich habe viele Fußballspiele gesehen, und zu keinem Zeitpunkt hat jemand von „Punkten im Quadrat“ gesprochen. Es ist keine echte Maßeinheit, und da die Varianz in dieser Kauderwelsch-Einheit ausgedrückt wird, ist sie für einen Menschen völlig bedeutungslos.

Standardabweichung

Okay, nehmen wir an, dass Ihnen die Idee, die Varianz zu verwenden, aufgrund der schönen mathematischen Eigenschaften, über die ich nicht gesprochen habe, gefällt. Aber da Sie ein Mensch und kein Roboter sind, möchten Sie ein Maß haben, das in denselben Einheiten wie die Daten selbst ausgedrückt wird (d. h. Punkte, nicht Punkte zum Quadrat). Was sollten Sie tun? Die Lösung des Problems ist offensichtlich! Nehmen Sie die Quadratwurzel der Varianz, bekannt als die Standardabweichung, auch „Wurzel der mittleren quadrierten Abweichung“ (root mean squared deviation) genannt. Damit ist unser Problem ziemlich gut gelöst. Während niemand eine Ahnung hat, was „eine Varianz von 324,68 Punkten zum Quadrat“ wirklich bedeutet, ist es viel einfacher, „eine Standardabweichung von 18,01 Punkten“ zu verstehen, da sie in den ursprünglichen Einheiten angegeben ist. Es ist üblich, die Standardabweichung einer Datenstichprobe als s zu bezeichnen, obwohl gelegentlich auch „sd“, „SD“ oder „Std. abw.“ (std dev.) verwendet werden.

Da die Standardabweichung gleich der Quadratwurzel der Varianz ist, wird es Sie wahrscheinlich nicht überraschen, dass die Formel so lautet:

\[s = \sqrt{ \frac{1}{N} \sum_{i=1}^N \left( X_i - \bar{X} \right)^2 }\]

und in jamovi gibt es eine Checkbox für Std. deviation direkt über der Checkbox für Variance. Wenn Sie diese auswählen, erhalten Sie einen Wert von 26,07 für die Standardabweichung.

Wie Sie vielleicht schon aus unserer Diskussion über die Varianz erraten haben, weicht die tatsächliche Berechnung von jamovi etwas von der oben angegebenen Formel ab. Wie wir bei der Varianz gesehen haben, berechnet jamovi eine Version, die durch N - 1 und nicht durch N dividiert.

Aus Gründen, die sinnvoll sind, wenn wir in Kapitel Schätzen unbekannter Größen anhand einer Stichprobe auf dieses Thema zurückkommen, werde ich diese neue Größe als :math:hatsigma` (gelesen als: „Sigma-Dach“) bezeichnen, und die Formel dafür lautet:

\[\hat\sigma = \sqrt{ \frac{1}{N - 1} \sum_{i=1}^N \left( X_i - \bar{X} \right)^2 }\]

Die Interpretation von Standardabweichungen ist etwas komplexer. Da die Standardabweichung von der Varianz abgeleitet wird und die Varianz eine Größe ist, die für uns Menschen wenig bis gar keine Bedeutung hat, lässt sich die Standardabweichung nicht einfach interpretieren. Folglich verlassen sich die meisten von uns auf eine einfache Faustregel. Im Allgemeinen sollte man erwarten, dass 68 % der Daten innerhalb von 1 Standardabweichung, 95 % der Daten innerhalb von 2 Standardabweichungen und 99,7 % der Daten innerhalb von 3 Standardabweichungen um den Mittelwert liegen. Diese Regel funktioniert in den meisten Fällen recht gut, ist aber nicht exakt. Sie wird auf der Grundlage der Annahme berechnet, dass das Histogramm symmetrisch und „glockenförmig“ ist.[3] Wie Sie anhand des Histogramms der AFL-Gewinnmargen in Abb. 20 sehen können, trifft dies auf unsere Daten eher nicht zu! Trotzdem ist die Regel ungefähr richtig. Wie sich herausstellt, liegen 65,3 % der AFL-Gewinnspannen innerhalb einer Standardabweichung vom Mittelwert. Dies wird in Abb. 14 visuell dargestellt.

Abb. 14 Illustration der Standardabweichung für die AFL-Gewinnspannen. Die schattierten Balken im Histogramm zeigen, wie viele der Daten innerhalb einer Standardabweichung vom Mittelwert liegen. In diesem Fall liegen 65,3 % des Datensatzes innerhalb dieses Bereichs, was ziemlich gut mit der im Haupttext besprochenen „ungefähr 68 %“-Regel übereinstimmt.

Welches Maß sollten wir verwenden?

Wir haben einige Streuungsmaße erörtert: Spannweite, IQR, mittlere absolute Abweichung, Varianz und Standardabweichung, und ihre Stärken und Schwächen angedeutet. Hier ist eine kurze Zusammenfassung:

• Spannweite. Zeigt die gesamte Bandbreite der Daten an. Er ist aber sehr anfällig für Ausreißer und wird daher nicht oft verwendet, es sei denn, Sie haben gute Gründe, sich um die Extreme in den Daten zu kümmern.

• Interquartilabstand. Gibt an, wo sich die „mittlere Hälfte“ der Daten befindet. Er ist ziemlich robust und ergänzt den Median gut. Dies wird häufig verwendet.

• Mittlere absolute Abweichung. Sie gibt an, wie weit die Beobachtungen „im Durchschnitt“ vom Mittelwert entfernt sind. Sie ist sehr gut interpretierbar, hat aber ein paar kleinere Probleme (die hier nicht diskutiert werden), die sie für Statistiker weniger attraktiv machen als die Standardabweichung. Wird manchmal verwendet, aber nicht oft.

• Varianz. Gibt die durchschnittliche quadrierte Abweichung vom Mittelwert an. Sie ist mathematisch elegant und wahrscheinlich der „richtige“ Weg, um die Abweichung vom Mittelwert zu beschreiben, aber sie ist völlig uninterpretierbar, weil sie nicht dieselben Einheiten wie die Daten verwendet. Sie wird fast nie verwendet, außer als mathematisches Hilfsmittel, aber sie steckt unter der Haube zahlreicher statistischer Werkzeuge.

• Standardabweichung. Dies ist die Quadratwurzel der Varianz. Sie ist mathematisch recht elegant und wird in denselben Einheiten wie die Daten ausgedrückt, so dass sie recht gut interpretiert werden kann. In Situationen, in denen der Mittelwert das Maß für die zentrale Tendenz ist, ist dies der Standardwert. Dies ist bei weitem das beliebteste Maß für die Variation.

Kurz gesagt, der IQR und die Standardabweichung sind die beiden gebräuchlichsten Maße zur Angabe der Variabilität der Daten. Es gibt aber auch Situationen, in denen die anderen Maße verwendet werden. Ich habe sie alle in diesem Buch beschrieben, weil die Wahrscheinlichkeit groß ist, dass Sie auf die meisten von ihnen stoßen werden.

---

[1]

Nun, ich werde ganz kurz diejenige erwähnen, die ich für die coolste halte, und zwar für eine ganz bestimmte Definition von „cool“. Varianzen sind additiv. Das bedeutet Folgendes: Angenommen, ich habe zwei Variablen X und Y, deren Varianzen jeweils Var(X) und Var(Y) sind. Nun stelle ich mir vor, dass ich eine neue Variable Z definieren möchte, welche die Summe der beiden ist, Z = X + Y. Wie sich herausstellt, ist die Varianz von Z gleich Var(X) + Var(Y). Dies ist eine sehr nützliche Eigenschaft, aber sie gilt nicht für die anderen Maße, über die ich in diesem Abschnitt spreche.

[2]

Mit der möglichen Ausnahme der dritten Frage.

[3]

Streng genommen geht man davon aus, dass die Daten normalverteilt sind. Dies ist ein wichtiges Konzept, auf das wir in Kapitel Einführung in die Wahrscheinlichkeitsrechnung näher eingehen werden und das im weiteren Verlauf des Buches immer wieder auftauchen wird.