Section author: Danielle J. Navarro and David R. Foxcroft

Model checking

The main focus of this section is regression diagnostics, a term that refers to the art of checking that the assumptions of your regression model have been met, figuring out how to fix the model if the assumptions are violated, and generally to check that nothing “funny” is going on. I refer to this as the “art” of model checking with good reason. It’s not easy, and while there are a lot of fairly standardised tools that you can use to diagnose and maybe even cure the problems that ail your model (if there are any, that is!), you really do need to exercise a certain amount of judgement when doing this. It’s easy to get lost in all the details of checking this thing or that thing, and it’s quite exhausting to try to remember what all the different things are. This has the very nasty side effect that a lot of people get frustrated when trying to learn all the tools, so instead they decide not to do any model checking. This is a bit of a worry!

In this section I describe several different things you can do to check that your regression model is doing what it’s supposed to. It doesn’t cover the full space of things you could do, but it’s still much more detailed than what I see a lot of people doing in practice, and even I don’t usually cover all of this in my intro stats class either. However, I do think it’s important that you get a sense of what tools are at your disposal, so I’ll try to introduce a bunch of them here. Finally, I should note that this section draws quite heavily from Fox and Weisberg (2011), the book associated with the car package that is used to conduct regression analysis in R. The car package is notable for providing some excellent tools for regression diagnostics, and the book itself talks about them in an admirably clear fashion. I don’t want to sound too gushy about it, but I do think that Fox and Weisberg (2011) is well worth reading, even if some of the advanced diagnostic techniques are only available in R and not jamovi.

Three kinds of residuals

The majority of regression diagnostics revolve around looking at the residuals, and by now you’ve probably formed a sufficiently pessimistic theory of statistics to be able to guess that, precisely because of the fact that we care a lot about the residuals, there are several different kinds of residual that we might consider. In particular, the following three kinds of residuals are referred to in this section: “ordinary residuals”, “standardised residuals”, and “Studentised residuals”. There is a fourth kind that you’ll see referred to in some of the Figures, and that’s the “Pearson residual”. However, for the models that we’re talking about in this chapter, the Pearson residual is identical to the ordinary residual.

The first and simplest kind of residuals that we care about are ordinary residuals. These are the actual raw residuals that I’ve been talking about throughout this chapter so far. The ordinary residual is just the difference between the fitted value Ŷ_i and the observed value Y_i. I’ve been using the notation ε_i to refer to the i-th ordinary residual, and by gum I’m going to stick to it. With this in mind, we have the very simple equation:

ε_i = Y_i - Ŷ_i

This is of course what we saw earlier, and unless I specifically refer to some other kind of residual, this is the one I’m talking about. So there’s nothing new here. I just wanted to repeat myself. One drawback to using ordinary residuals is that they’re always on a different scale, depending on what the outcome variable is and how good the regression model is. That is, unless you’ve decided to run a regression model without an intercept term, the ordinary residuals will have mean 0 but the variance is different for every regression. In a lot of contexts, especially where you’re only interested in the pattern of the residuals and not their actual values, it’s convenient to estimate the standardised residuals, which are normalised in such a way as to have standard deviation 1.

The way we calculate these is to divide the ordinary residual by an estimate of the (population) standard deviation of these residuals. For technical reasons, mumble mumble, the formula for this is

ε_i’ = \(\frac{\epsilon_i}{\hat{\sigma} \sqrt{1-h_i}}\)

where \(\hat\sigma\) in this context is the estimated population standard deviation of the ordinary residuals, and h_i is the “hat value” of the i-th observation. I haven’t explained hat values to you yet (but have no fear,[1] it’s coming shortly), so this won’t make a lot of sense. For now, it’s enough to interpret the standardised residuals as if we’d converted the ordinary residuals to z-scores. In fact, that is more or less the truth, it’s just that we’re being a bit fancier.

The third kind of residuals are Studentised residuals (also called “jackknifed residuals”) and they’re even fancier than standardised residuals. Again, the idea is to take the ordinary residual and divide it by some quantity in order to estimate some standardised notion of the residual.

The formula for doing the calculations this time is subtly different

\[\epsilon_{i}^* = \frac{\epsilon_i}{\hat{\sigma}_{(-i)} \sqrt{1-h_i}}\]

Notice that our estimate of the standard deviation here is written \(\hat{\sigma}_{(-i)}\). What this corresponds to is the estimate of the residual standard deviation that you would have obtained if you just deleted the ith observation from the data set. This sounds like the sort of thing that would be a nightmare to calculate, since it seems to be saying that you have to run N new regression models (even a modern computer might grumble a bit at that, especially if you’ve got a large data set). Fortunately, some terribly clever person has shown that this standard deviation estimate is actually given by the following equation:

\[\hat\sigma_{(-i)} = \hat{\sigma} \ \sqrt{\frac{N-K-1 - {\epsilon_{i}^\prime}^2}{N-K-2}}\]

Isn’t that a pip?

Before moving on, I should point out that you don’t often need to obtain these residuals yourself, even though they are at the heart of almost all regression diagnostics. Most of the time the various options that provide the diagnostics, or assumption checks, will take care of these calculations for you. Even so, it’s always nice to know how to actually get hold of these things yourself in case you ever need to do something non-standard.

Three kinds of anomalous data

One danger that you can run into with linear regression models is that your analysis might be disproportionately sensitive to a smallish number of “unusual” or “anomalous” observations. I discussed this idea previously in subsection Using box plots to detect outliers in the context of discussing the outliers that get automatically identified by the Box plot option under Exploration → Descriptives, but this time we need to be much more precise. In the context of linear regression, there are three conceptually distinct ways in which an observation might be called “anomalous”. All three are interesting, but they have rather different implications for your analysis.

The first kind of unusual observation is an outlier. The definition of an outlier (in this context) is an observation that is very different from what the regression model predicts. An example is shown in Fig. 122. In practice, we operationalise this concept by saying that an outlier is an observation that has a very large Studentised residual, ε_i^*. Outliers are interesting: a big outlier might correspond to junk data, e.g., the variables might have been recorded incorrectly in the data set, or some other defect may be detectable. Note that you shouldn’t throw an observation away just because it’s an outlier. But the fact that it’s an outlier is often a cue to look more closely at that case and try to find out why it’s so different.

Fig. 122 Illustration of outliers: The dotted lines plot the regression line that would have been estimated without the anomalous observation included, and the corresponding residual (i.e., the Studentised residual). The solid line shows the regression line with the anomalous observation included. The outlier has an unusual value on the outcome (y axis location) but not the predictor (x axis location), and lies a long way from the regression line.

Fig. 123 Illustration of high leverage points: The anomalous observation in this case is unusual both in terms of the predictor (x axis) and the outcome (y axis), but this unusualness is highly consistent with the pattern of correlations that exists among the other observations. The observation falls very close to the regression line and does not distort it.

The second way in which an observation can be unusual is if it has high leverage, which happens when the observation is very different from all the other observations. This doesn’t necessarily have to correspond to a large residual. If the observation happens to be unusual on all variables in precisely the same way, it can actually lie very close to the regression line. An example of this is shown in Fig. 123. The leverage of an observation is operationalised in terms of its hat value, usually written h_i. The formula for the hat value is rather complicated,[2] but it interpretation is not: h_i is a measure of the extent to which the i-th observation is “in control” of where the regression line ends up going.

In general, if an observation lies far away from the other ones in terms of the predictor variables, it will have a large hat value (as a rough guide, high leverage is when the hat value is more than 2 - 3 times the average; and note that the sum of the hat values is constrained to be equal to K + 1). High leverage points are also worth looking at in more detail, but they’re much less likely to be a cause for concern unless they are also outliers.

Fig. 124 Illustration of high influence points: In this case, the anomalous observation is highly unusual on the predictor variable (x axis), and falls a long way from the regression line. As a consequence, the regression line is highly distorted, even though (in this case) the anomalous observation is entirely typical in terms of the outcome variable (y axis).

This brings us to our third measure of unusualness, the influence of an observation. A high influence observation is an outlier that has high leverage. That is, it is an observation that is very different to all the other ones in some respect, and also lies a long way from the regression line. This is illustrated in Fig. 124. Notice the contrast to the previous two figures. Outliers don’t move the regression line much and neither do high leverage points. But something that is both an outlier and has high leverage, well that has a big effect on the regression line. That’s why we call these points high influence, and it’s why they’re the biggest worry. We operationalise influence in terms of a measure known as Cook’s distance.

\[D_i = \frac{{\epsilon_i^*}^2 }{K+1} \times \frac{h_i}{1-h_i}\]

Notice that this is a multiplication of something that measures the outlier-ness of the observation (the bit on the left), and something that measures the leverage of the observation (the bit on the right).

In order to have a large Cook’s distance an observation must be a fairly substantial outlier and have high leverage. As a rough guide, Cook’s distance greater than 1 is often considered large (that’s what I typically use as a quick and dirty rule).

In jamovi, information about Cook’s distance can be calculated by clicking on the Cook’s Distance checkbox in the Assumption Checks → Data Summary options. When you do this, for the multiple regression model we have been using as an example in this chapter, you get the results as shown in Fig. 125.

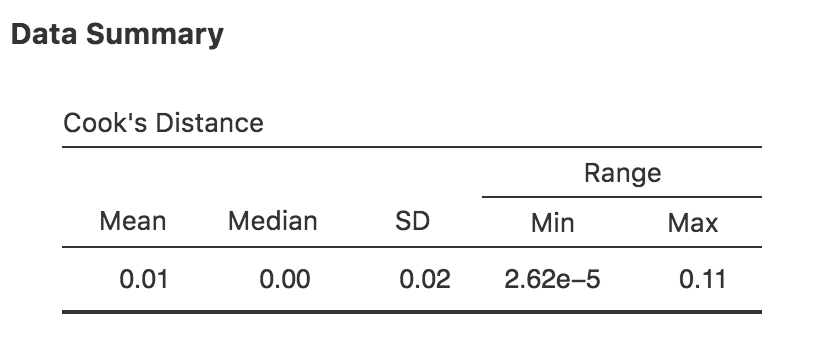
Fig. 125 jamovi output showing the table for the Cook’s distance statistics

You can see that, in this example, the mean Cook’s distance value is 0.01, and the range is from 0.00000262 to 0.11, so this is some way off the rule of thumb figure mentioned above that a Cook’s distance greater than 1 is considered large.

An obvious question to ask next is, if you do have large values of Cook’s distance what should you do? As always, there’s no hard and fast rule. Probably the first thing to do is to try running the regression with the outlier with the greatest Cook’s distance[3] excluded and see what happens to the model performance and to the regression coefficients. If they really are substantially different, it’s time to start digging into your data set and your notes that you no doubt were scribbling as your ran your study. Try to figure out why the point is so different. If you start to become convinced that this one data point is badly distorting your results then you might consider excluding it, but that’s less than ideal unless you have a solid explanation for why this particular case is qualitatively different from the others and therefore deserves to be handled separately.

Checking the normality of the residuals

Like many of the statistical tools we’ve discussed in this book, regression models rely on a normality assumption. In this case, we assume that the residuals are normally distributed. The first thing we can do is draw a QQ-plot via the Assumption Checks → Q-Q plot of residuals option.

The output is shown in Fig. 126, showing the standardised residuals plotted as a function of their theoretical quantiles according to the regression model.

Fig. 126 Plot of the theoretical quantiles according to the model, against the quantiles of the standardised residuals, produced in jamovi

Another thing we should check is the relationship between the fitted values and the residuals themselves. We can get jamovi to do this using the Residuals Plots option, which provides a scatterplot for each predictor variable, the outcome variable, and the fitted values against residuals, see Fig. 127. In these plots we are looking for a fairly uniform distribution of “dots”, with no clear bunching or patterning of the “dots”. Looking at these plots, there is nothing particularly worrying as the dots are fairly evenly spread across the whole plot. There may be a little bit of non-uniformity in the right panel, but it is not a strong deviation and probably not worth worrying about.

Fig. 127 Residuals plots produced in jamovi

If we were worried, then in a lot of cases the solution to this problem (and many others) is to transform one or more of the variables. We discussed the basics of variable transformation in the sections Transforming and recoding a variable and Mathematical functions and operations, but I do want to make special note of one additional possibility that I didn’t explain fully earlier: the Box-Cox transform.

The Box-Cox function is a fairly simple one and it’s very widely used.

\[f(x,\lambda) = \frac{x^\lambda - 1}{\lambda}\]

for all values of λ except λ = 0. When λ = 0 we just take the natural logarithm (i.e., ln(x)).

You can calculate it using the BOXCOX function in the Compute variables screen in jamovi.

Checking for collinearity

The last kind of regression diagnostic that I’m going to discuss in this chapter is the use of variance inflation factors (VIFs), which are useful for determining whether or not the predictors in your regression model are too highly correlated with each other. There is a variance inflation factor associated with each predictor X_k in the model.

The formula for the k-th VIF is:

VIF_k = 1 / (1 - R²_(-k))

where R²_(-k) refers to R-squared value you would get if you ran a regression using X_k as the outcome variable, and all the other X variables as the predictors. The idea here is that R²_(-k) is a very good measure of the extent to which X_k is correlated with all the other variables in the model.

The square root of the VIF is pretty interpretable. It tells you how much wider the confidence interval for the corresponding coefficient b_k is, relative to what you would have expected if the predictors are all nice and uncorrelated with one another. If you’ve only got two predictors, the VIF values are always going to be the same, as we can see if we click on the Collinearity checkbox in the Regression → Assumption Checks options in jamovi. For both dani.sleep and baby.sleep the VIF is 1.65. And since the square root of 1.65 is 1.28, we see that the correlation between our two predictors isn’t causing much of a problem.

To give a sense of how we could end up with a model that has bigger collinearity problems, suppose I were to run a much less interesting regression model, in which I tried to predict the day on which the data were collected, as a function of all the other variables in the data set. To see why this would be a bit of a problem, let’s have a look at the correlation matrix for all four variables:

             dani.sleep  baby.sleep  dani.grump         day
dani.sleep   1.00000000  0.62794934 -0.90338404 -0.09840768
baby.sleep   0.62794934  1.00000000 -0.56596373 -0.01043394
dani.grump  -0.90338404 -0.56596373  1.00000000  0.07647926
day         -0.09840768 -0.01043394  0.07647926  1.00000000

We have some fairly large correlations between some of our predictor variables! When we run the regression model and look at the VIF values, we see that the collinearity is causing a lot of uncertainty about the coefficients. First, run the regression, as in Fig. 128 and you can see from the VIF values that, yep, that’s some mighty fine collinearity there.

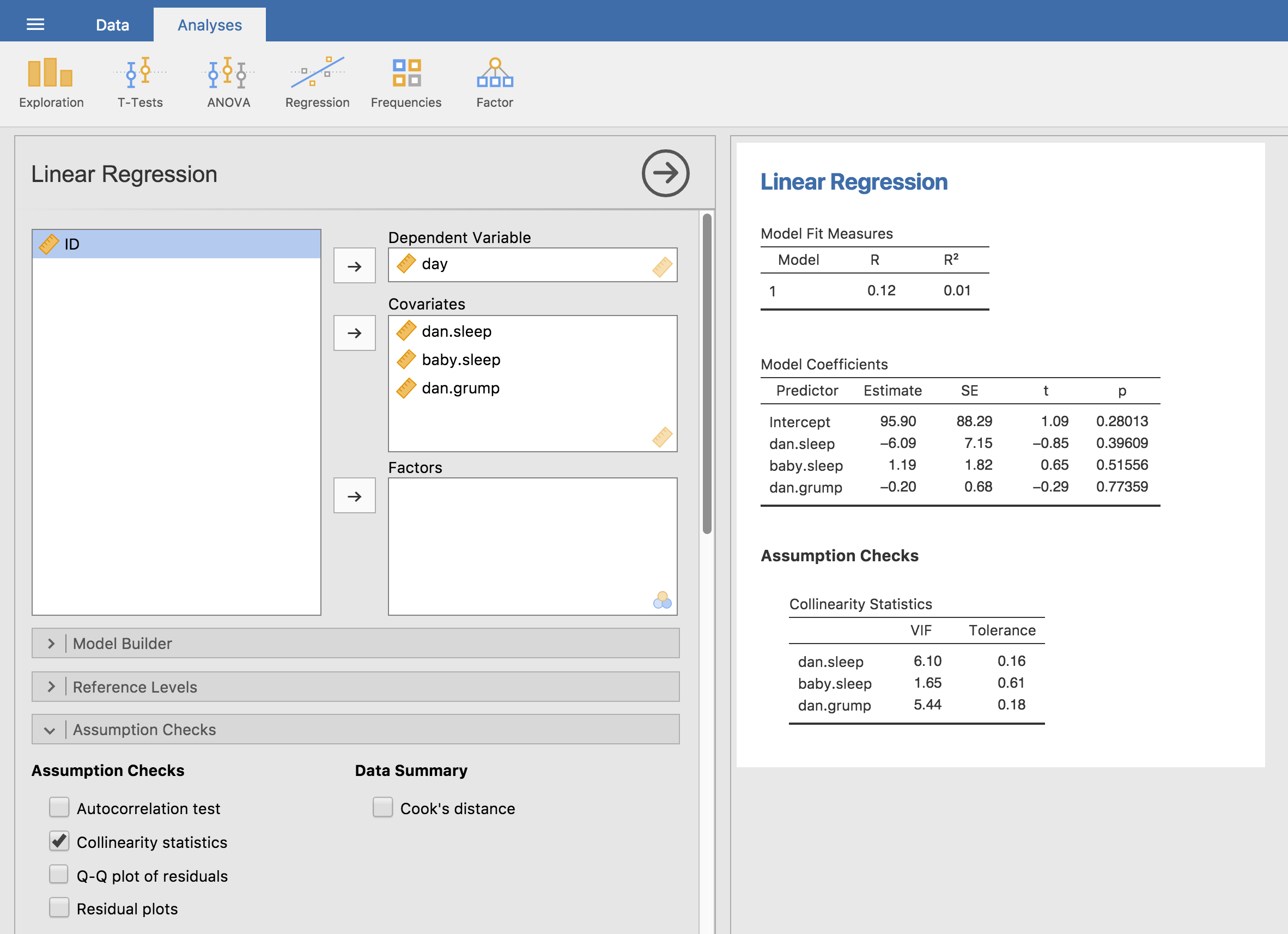
Fig. 128 Collinearity statistics for multiple regression, produced in jamovi

---

[1]	Or have no hope, as the case may be.

[2]

Again, for the linear algebra fanatics: the “hat matrix” is defined to be that matrix H that converts the vector of observed values y into a vector of fitted values ŷ, such that ŷ = Hy. The name comes from the fact that this is the matrix that “puts a hat on y”. The hat value of the i-th observation is the i-th diagonal element of this matrix (so technically I should be writing it as hii rather than hi). Oh, and in case you care, here’s how it’s calculated: H = X(X’X)-1 X’. Pretty, isn’t it?

[3]

In order to obtain the Cook’s distance for each participant, open the drop-down menu Save within the Linear Regression analysis options and set the check box Cook's distance. A new column containing Cook’s distances will be added at the end of your data set. Those values can then be used in connection with a filter to select participants.