Section author: Danielle J. Navarro and David R. Foxcroft

Correlations

In this section we’ll talk about how to describe the relationships between variables in the data. To do that, we want to talk mostly about the correlation between variables. But first, we need some data.

The data

Table 13 Descriptive statistics for the parenthood data set.

Variable	min	max	mean	median	std. dev	IQR
Dani’s grumpiness	41	91	63.71	62	10.05	14
Dani’s hours slept	4.84	9.00	6.97	7.03	1.02	1.45
Dani’s son’s hours slept	3.25	12.07	8.05	7.95	2.07	3.21

Let’s turn to a topic close to every parent’s heart: sleep. The data set we’ll use is fictitious, but based on real events. Suppose I’m curious to find out how much my infant son’s sleeping habits affect my mood. Let’s say that I can rate my grumpiness very precisely, on a scale from 0 (not at all grumpy) to 100 (grumpy as a very, very grumpy old man or woman). And lets also assume that I’ve been measuring my grumpiness, my sleeping patterns and my son’s sleeping patterns for 100 days. The data are stored in the parenthood data set, that contains four variables dani.sleep, baby.sleep, dani.grump and day.

Next, I’ll take a look at some basic descriptive statistics and, to give a graphical depiction of what each of the three interesting variables looks like, Fig. 106 plots histograms. One thing to note: just because jamovi can calculate dozens of different statistics doesn’t mean you should report all of them. If I were writing this up for a report, I’d probably pick out those statistics that are of most interest to me (and to my readership), and then put them into a nice, simple table like the one in Table 13.[1] Notice that when I put it into a table, I gave everything “human readable” names. This is always good practice. Notice also that I’m not getting enough sleep. This isn’t good practice, but other parents tell me that it’s pretty standard.

Fig. 106 Histograms for the three interesting variables in the parenthood data set

The strength and direction of a relationship

We can draw scatterplots to give us a general sense of how closely related two variables are. Ideally though, we might want to say a bit more about it than that. For instance, let’s compare the relationship between dani.sleep and dani.grump (Fig. 107, left) with that between baby.sleep and dani.grump (Fig. 107, right). When looking at these two plots side by side, it’s clear that the relationship is qualitatively the same in both cases: more sleep equals less grump! However, it’s also pretty obvious that the relationship between dani.sleep and dani.grump is stronger than the relationship between baby.sleep and dani.grump. The plot on the left is “neater” than the one on the right. What it feels like is that if you want to predict what my mood is, it’d help you a little bit to know how many hours my son slept, but it’d be more helpful to know how many hours I slept.

Fig. 107 Scatterplots showing the relationship between dani.sleep and dani.grump (left panel) and the relationship between baby.sleep and dani.grump (right panel).

In contrast, let’s consider the two scatterplots shown in Fig. 108. If we compare the scatterplot of baby.sleep vs. dani.grump (left) to the scatterplot of baby.sleep vs. dani.sleep (right), the overall strength of the relationship is the same, but the direction is different. That is, if my son sleeps more, I get more sleep (positive relationship, right hand side), but if he sleeps more then I get less grumpy (negative relationship, left hand side).

Fig. 108 Scatterplots showing the relationship between baby.sleep and dani.grump (left panel) and the relationship between baby.sleep and dani.sleep (right panel).

The correlation coefficient

We can make these ideas a bit more explicit by introducing the idea of a correlation coefficient (or, more specifically, Pearson’s correlation coefficient), which is traditionally denoted as r. The correlation coefficient between two variables X and Y (sometimes denoted r_XY), which we’ll define more precisely in the next section, is a measure that varies from -1 to 1. When r = -1 it means that we have a perfect negative relationship, and when r = 1 it means we have a perfect positive relationship. When r = 0, there’s no relationship at all. If you look at Fig. 109, you can see several plots showing what different correlations look like.

Fig. 109 Illustration of the effect of varying the strength and direction of a correlation. In the left hand column, the correlations are 0.00, 0.33, 0.67 and 1.00 In the right hand column, the correlations are 0.00, -0.33, -0.67 and -1.00.

The formula for the Pearson’s correlation coefficient can be written in several different ways. I think the simplest way to write down the formula is to break it into two steps. Firstly, let’s introduce the idea of a covariance. The covariance between two variables X and Y is a generalisation of the notion of the variance amd is a mathematically simple way of describing the relationship between two variables that isn’t terribly informative to humans

\[\mbox{Cov}(X,Y) = \frac{1}{N-1} \sum_{i=1}^N \left(X_i - \bar{X} \right) \left(Y_i - \bar{Y} \right)\]

Because we’re multiplying (i.e., taking the “product” of) a quantity that depends on X by a quantity that depends on Y and then averaging,[2] you can think of the formula for the covariance as an “average cross product” between X and Y.

The covariance has the nice property that, if X and Y are entirely unrelated, then the covariance is exactly zero. If the relationship between them is positive (in the sense shown in Fig. 109) then the covariance is also positive, and if the relationship is negative then the covariance is also negative. In other words, the covariance captures the basic qualitative idea of correlation. Unfortunately, the raw magnitude of the covariance isn’t easy to interpret as it depends on the units in which X and Y are expressed and, worse yet, the actual units that the covariance itself is expressed in are really weird. For instance, if X refers to the dani.sleep variable (units: hours) and Y refers to the dani.grump variable (units: grumps), then the units for their covariance are “hours × grumps”. And I have no freaking idea what that would even mean.

The Pearson correlation coefficient r fixes this interpretation problem by standardising the covariance, in pretty much the exact same way that the z-score standardises a raw score, by dividing by the standard deviation. However, because we have two variables that contribute to the covariance, the standardisation only works if we divide by both standard deviations.[3] In other words, the correlation between X and Y can be written as follows:

\[r_{XY} = \frac{\mbox{Cov}(X,Y)}{ \hat{\sigma}_X \ \hat{\sigma}_Y}\]

By standardising the covariance, not only do we keep all of the nice properties of the covariance discussed earlier, but the actual values of r are on a meaningful scale: r = 1 implies a perfect positive relationship and r = -1 implies a perfect negative relationship. I’ll expand a little more on this point later, in subsection Interpreting a correlation. But before I do, let’s look at how to calculate correlations in jamovi.

Calculating correlations in jamovi

Calculating correlations in jamovi can be done by clicking on the Regression → Correlation Matrix button. Transfer all four continuous variables across into the box on the right to get the output in Fig. 110.

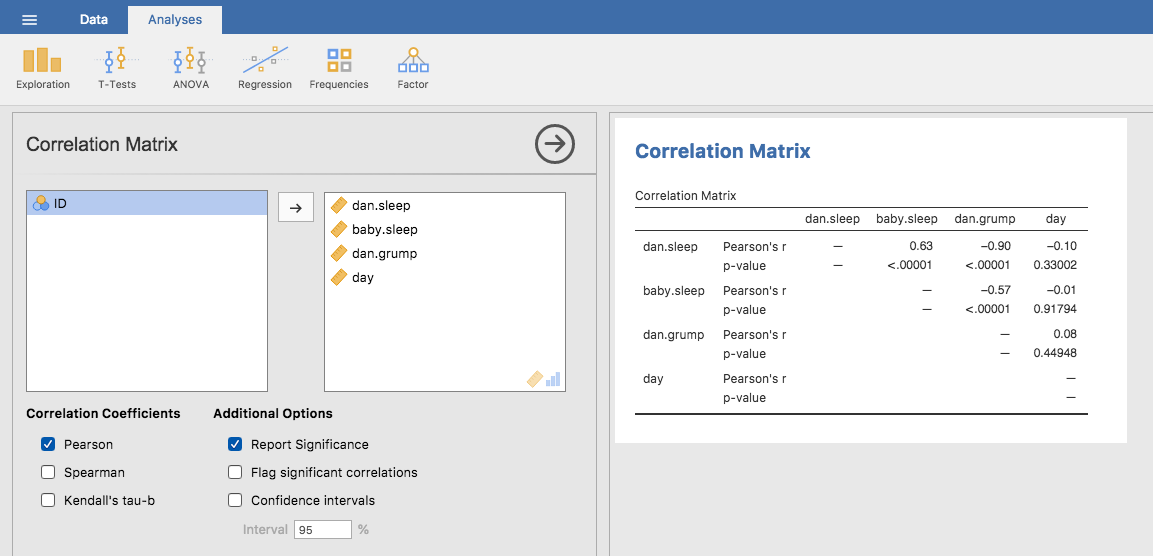
Fig. 110 jamovi screenshot showing correlations between variables in the parenthood data set

Interpreting a correlation

Naturally, in real life you don’t see many correlations of 1. So how should you interpret a correlation of, say, r = 0.4? The honest answer is that it really depends on what you want to use the data for, and on how strong the correlations in your field tend to be. A friend of mine in engineering once argued that any correlation less than 0.95 is completely useless (I think he was exaggerating, even for engineering). On the other hand, there are real cases, even in psychology, where you should really expect correlations that strong. For instance, one of the benchmark data sets used to test theories of how people judge similarities is so clean that any theory that can’t achieve a correlation of at least 0.9 really isn’t deemed to be successful. However, when looking for (say) elementary correlates of intelligence (e.g., inspection time, response time), if you get a correlation above 0.3 you’re doing very very well. In short, the interpretation of a correlation depends a lot on the context. That said, the rough guide in Table 14 is pretty typical.

Table 14 A rough guide to interpreting correlations. Note that I say a rough guide. There aren’t hard and fast rules for what counts as strong or weak relationships. It depends on the context.

Correlation	Strength	Direction
-1.0 to -0.9	Very strong	Negative
-0.9 to -0.7	Strong	Negative
-0.7 to -0.4	Moderate	Negative
-0.4 to -0.2	Weak	Negative
-0.2 to 0.0	Negligible	Negative
0.0 to 0.2	Negligible	Positive
0.2 to 0.4	Weak	Positive
0.4 to 0.7	Moderate	Positive
0.7 to 0.9	Strong	Positive
0.9 to 1.0	Very strong	Positive

Fig. 111 Anscombe’s quartet: All four of these data sets have a Pearson correlation of r = 0.816, but they are qualitatively different from one another.

However, something that can never be stressed enough is that you should always look at the scatterplot before attaching any interpretation to the data. A correlation might not mean what you think it means. The classic illustration of this is “Anscombe’s Quartet” (Anscombe, 1973), a collection of four data sets. Each data set has two variables, an X and a Y. For all four data sets the mean value for X is 9 and the mean for Y is 7.5. The standard deviations for all X variables are almost identical, as are those for the Y variables. And in each case the correlation between X and Y is r = 0.816`. You can verify this yourself, since I happen to have saved it as a dataset called anscombe.

You’d think that these four data sets would look pretty similar to one another. They do not. If we draw scatterplots of X against Y for all four variables, as shown in Fig. 111, we see that all four of these are spectacularly different to each other. The lesson here, which so very many people seem to forget in real life, is always graph your raw data (chapter Drawing graphs).

Spearman’s rank correlations

The Pearson correlation coefficient is useful for a lot of things, but it does have shortcomings. One issue in particular stands out: what it actually measures is the strength of the linear relationship between two variables. In other words, what it gives you is a measure of the extent to which the data all tend to fall on a single, perfectly straight line. Often, this is a pretty good approximation to what we mean when we say “relationship”, and so the Pearson correlation is a good thing to calculate. Sometimes though, it isn’t.

One very common situation where the Pearson correlation isn’t quite the right thing to use arises when an increase in one variable X really is reflected in an increase in another variable Y, but the nature of the relationship isn’t necessarily linear. An example of this might be the relationship between effort and reward when studying for an exam. If you put zero effort (X) into learning a subject then you should expect a grade of 0% (Y). However, a little bit of effort will cause a massive improvement. Just turning up to lectures means that you learn a fair bit, and if you just turn up to classes and scribble a few things down your grade might rise to 35%, all without a lot of effort. However, you just don’t get the same effect at the other end of the scale. As everyone knows, it takes a lot more effort to get a grade of 90% than it takes to get a grade of 55%. What this means is that, if I’ve got data looking at study effort and grades, there’s a pretty good chance that Pearson correlations will be misleading.

To illustrate, consider the data plotted in Fig. 112, showing the relationship between hours worked and grade received for 10 students taking some class. The curious thing about this (highly fictitious) data set is that increasing your effort always increases your grade. It might be by a lot or it might be by a little, but increasing effort will never decrease your grade. If we run a standard Pearson correlation, it shows a strong relationship between hours worked and grade received, with a correlation coefficient of 0.91. However, this doesn’t actually capture the observation that increasing hours worked always increases the grade. There’s a sense here in which we want to be able to say that the correlation is perfect but for a somewhat different notion of what a “relationship” is. What we’re looking for is something that captures the fact that there is a perfect ordinal relationship here. That is, if student 1 works more hours than student 2, then we can guarantee that student 1 will get the better grade. That’s not what a correlation of r = 0.91 says at all.

Fig. 112 The relationship between hours worked and grade received for a toy data set consisting of only 10 students (each circle corresponds to one student). The dashed line through the middle shows the linear relationship between the two variables. This produces a strong Pearson correlation of r = 0.91. However, the interesting thing to note here is that there’s actually a perfect monotonic relationship between the two variables. In this toy example, increasing the hours worked always increases the grade received, as illustrated by the solid line. This is reflected in a Spearman correlation of ρ = 1.00. With such a small data set, however, it’s an open question as to which version better describes the actual relationship involved.

How should we address this? Actually, it’s really easy. If we’re looking for ordinal relationships all we have to do is treat the data as if it were ordinal scale ! So, instead of measuring effort in terms of “hours worked”, lets rank all 10 of our students in order of hours worked. That is, student 1 did the least work out of anyone (2 hours) so they get the lowest rank (rank = 1). Student 4 was the next laziest, putting in only 6 hours of work over the whole semester, so they get the next lowest rank (rank = 2). Notice that I’m using “rank =1” to mean “low rank”. Sometimes in everyday language we talk about “rank = 1” to mean “top rank” rather than “bottom rank”. So be careful, you can rank “from smallest value to largest value” (i.e., small equals rank 1) or you can rank “from largest value to smallest value” (i.e., large equals rank 1). In this case, I’m ranking from smallest to largest, but as it’s really easy to forget which way you set things up you have to put a bit of effort into remembering!

Okay, so let’s have a look at our students when we rank them from worst to best in terms of effort and reward:

	rank (hours worked)	rank (grade received)
student 1	1	1
student 2	10	10
student 3	6	6
student 4	2	2
student 5	3	3
student 6	5	5
student 7	4	4
student 8	8	8
student 9	7	7
student 10	9	9

Hmm. These are identical. The student who put in the most effort got the best grade, the student with the least effort got the worst grade, etc. As the table above shows, these two rankings are identical, so if we now correlate them we get a perfect relationship, with a correlation of 1.0.

What we’ve just re-invented is Spearman’s rank order correlation, usually denoted ρ to distinguish it from the Pearson correlation r. We can calculate Spearman’s ρ using jamovi simply by clicking the Spearman check box in the Correlation Matrix options panel.

---

[1]	Actually, even that table is more than I’d bother with. In practice, most people pick one measure of central tendency, and one measure of variability only.

[2]	Just like we saw with the variance and the standard deviation, in practice we divide by N - 1 rather than N.

[3]	This is an oversimplification, but it’ll do for our purposes.