Section author: Danielle J. Navarro and David R. Foxcroft

One-sided tests

When introducing the theory of null hypothesis tests, I mentioned that there are some situations when it’s appropriate to specify a one-sided test (see section The difference between one-sided and two-sided tests). So far all of the t-tests have been two-sided tests. For instance, when we specified a one sample t-test for the grades in Dr Zeppo’s class the null hypothesis was that the true mean was 67.5%. The alternative hypothesis was that the true mean was greater than or less than 67.5%. Suppose we were only interested in finding out if the true mean is greater than 67.5%, and have no interest whatsoever in testing to find out if the true mean is lower than 67.5%. If so, our null hypothesis would be that the true mean is 67.5% or less, and the alternative hypothesis would be that the true mean is greater than 67.5%. In jamovi, for the One Sample T-Test analysis, you can specify this by clicking on the > Test Value option, under Hypothesis. When you have done this, you will get the results as shown in Fig. 98.

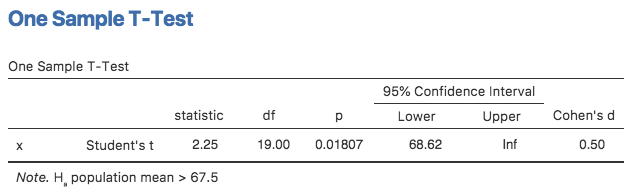
Fig. 98 jamovi results showing a One Sample T-Test where the actual hypothesis is one-sided, i.e. that the true mean is greater than 67.5%.

Notice that there are a few changes from the output that we saw last time. Most important is the fact that the actual hypothesis has changed, to reflect the different test. The second thing to note is that although the t-statistic and degrees of freedom have not changed, the p-value has. This is because the one-sided test has a different rejection region from the two-sided test. If you’ve forgotten why this is and what it means, you may find it helpful to read back over chapter Hypothesis testing, and section The difference between one-sided and two-sided tests in particular. The third thing to note is that the confidence interval is different too: it now reports a “one-sided” confidence interval rather than a two-sided one. In a two-sided confidence interval we’re trying to find numbers a and b such that we’re confident that, if we were to repeat the study many times, then 95% of the time the mean would lie between a and b. In a one-sided confidence interval, we’re trying to find a single number a such that we’re confident that 95% of the time the true mean would be greater than a (or less than a if you selected Measure 1 < Measure 2 in the Hypothesis section).

So that’s how to do a one-sided one sample t-test. However, all versions of the t-test can be one-sided. For an independent samples t-test, you could have a one-sided test if you’re only interested in testing to see if group A has higher scores than group B, but have no interest in finding out if group B has higher scores than group A. Let’s suppose that, for Dr Harpo’s class, you wanted to see if Anastasia’s students had higher grades than Bernadette’s. For this analysis, in the Hypothesis options, specify that Group 1 > Group2. You should get the results shown in Fig. 99.

Fig. 99 jamovi results showing an Independent Samples T-Test where the actual hypothesis is one-sided, i.e. that Anastasia’s students had higher grades than Bernadette’s.

Again, the output changes in a predictable way. The definition of the alternative hypothesis has changed, the p-value has changed, and it now reports a one-sided confidence interval rather than a two-sided one.

What about the paired samples t-test? Suppose we wanted to test the hypothesis that grades go up from test 1 to test 2 in Dr Zeppo’s class, and are not prepared to consider the idea that the grades go down. In jamovi you would do this by specifying, under the Hypotheses option, that grade_test2 (Measure 1 in jamovi, because we copied this first into the paired variables box) > grade_test1 (Measure 2 in jamovi). You should get the results shown in Fig. 100.

Fig. 100 jamovi results showing a Paired Samples T-Test where the actual hypothesis is one-sided, i.e. that grade test2 (Measure 1) is larger than grade test1 (Measure 2).

Yet again, the output changes in a predictable way. The hypothesis has changed, the p-value has changed, and the confidence interval is now one-sided.