Section author: Danielle J. Navarro and David R. Foxcroft
The Fisher exact test¶
What should you do if your cell counts are too small, but you’d still like to
test the null hypothesis that the two variables are independent? One answer
would be “collect more data”, but that’s far too glib. There are a lot of
situations in which it would be either infeasible or unethical do that. If so,
statisticians have a kind of moral obligation to provide scientists with
better tests. In this instance, Fisher (1922a) kindly
provided the right answer to the question. To illustrate the basic idea let’s
suppose that we’re analysing data from a field experiment looking at the
emotional status of people who have been accused of Witchcraft, some of whom
are currently being burned at the stake.[1] Unfortunately for the scientist
(but rather fortunately for the general populace), it’s actually quite hard to
find people in the process of being set on fire, so the cell counts are
awfully small in some cases. A contingency table of the salem data set
illustrates the point:
on.fire
happy FALSE TRUE
FALSE 3 3
TRUE 10 0
Looking at this data, you’d be hard pressed not to suspect that people not on fire are more likely to be happy than people on fire. However, the χ²-test makes this very hard to test because of the small sample size. So, speaking as someone who doesn’t want to be set on fire, I’d really like to be able to get a better answer than this. This is where Fisher’s exact test (Fisher, 1922a) comes in very handy.
The Fisher exact test works somewhat differently to the χ²-test (or in fact any of the other hypothesis tests that I talk about in this book) insofar as it doesn’t have a test statistic, but it calculates the p-value “directly”. I’ll explain the basics of how the test works for a 2 × 2 contingency table. As before, let’s have some notation:
| Happy | Sad | Total | |
|---|---|---|---|
| Set on fire | O11 | O12 | R1 |
| Not set on fire | O21 | O22 | R2 |
| Total | C1 | C2 | N |
In order to construct the test Fisher treats both the row and column totals (R1, R2, C1 and C2) as known, fixed quantities and then calculates the probability that we would have obtained the observed frequencies that we did (O11, O12, O21 and O22) given those totals. In the notation that we developed in chapter Introduction to probability this is written:
and as you might imagine, it’s a slightly tricky exercise to figure out what this probability is. But it turns out that this probability is described by a distribution known as the hypergeometric distribution. What we have to do to calculate our p-value is calculate the probability of observing this particular table or a table that is “more extreme”.[2] Back in the 1920s, computing this sum was daunting even in the simplest of situations, but these days it’s pretty easy as long as the tables aren’t too big and the sample size isn’t too large. The conceptually tricky issue is to figure out what it means to say that one contingency table is more “extreme” than another. The easiest solution is to say that the table with the lowest probability is the most extreme. This then gives us the p-value.
You can specify this test in jamovi from a check box in the Statistics
options of the Contingency Tables analysis. When you do this with the
salem data set, the Fisher's exact test statistic is shown in the
results. The main thing we’re interested in here is the p-value, which in
this case is small enough (p = 0.036) to justify rejecting the null
hypothesis that people on fire are just as happy as people not on fire
(see Fig. 79).
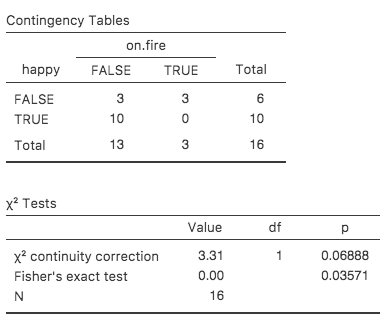
Fig. 79 Fisher's exact test output in jamovi. Ignore the Value and just
refer to the p-value
| [1] | This example is based on a joke article published in the Journal of Irreproducible Results. |
| [2] | Not surprisingly, the Fisher exact test is motivated by Fisher’s interpretation of a p-value, not Neyman’s! See section The p-value of a test. |