Section author: Danielle J. Navarro and David R. Foxcroft

Factorial ANOVA 3: unbalanced designs

Factorial ANOVA is a very handy thing to know about. It’s been one of the standard tools used to analyse experimental data for many decades, and you’ll find that you can’t read more than two or three papers in psychology without running into an ANOVA in there somewhere. However, there’s one huge difference between the ANOVAs that you’ll see in a lot of real scientific articles and the ANOVAs that I’ve described so far. In in real life we’re rarely lucky enough to have perfectly balanced designs. For one reason or another, it’s typical to end up with more observations in some cells than in others. Or, to put it another way, we have an unbalanced design.

Unbalanced designs need to be treated with a lot more care than balanced designs, and the statistical theory that underpins them is a lot messier. It might be a consequence of this messiness, or it might be a shortage of time, but my experience has been that undergraduate research methods classes in psychology have a nasty tendency to ignore this issue completely. A lot of stats textbooks tend to gloss over it too. The net result of this, I think, is that a lot of active researchers in the field don’t actually know that there’s several different “types” of unbalanced ANOVAs, and they produce quite different answers. In fact, reading the psychological literature, I’m kind of amazed at the fact that most people who report the results of an unbalanced factorial ANOVA don’t actually give you enough details to reproduce the analysis. I secretly suspect that most people don’t even realise that their statistical software package is making a whole lot of substantive data analysis decisions on their behalf. It’s actually a little terrifying when you think about it. So, if you want to avoid handing control of your data analysis to stupid software, read on.

The coffee data

As usual, it will help us to work with some data. The coffee data set contains a hypothetical data set that produces an unbalanced 3 × 2 ANOVA. Suppose we were interested in finding out whether or not the tendency of people to babble when they have too much coffee is purely an effect of the coffee itself, or whether there’s some effect of the milk and sugar that people add to the coffee. Suppose we took 18 people and gave them some coffee to drink. The amount of coffee, i.e., the caffeine, was held constant, and we varied whether or not milk was added, so milk is a binary factor with two levels, yes and no. We also varied the kind of sugar involved. The coffee might contain real sugar or it might contain fake sugar (i.e., artificial sweetener) or it might contain none at all, so the sugar variable is a three level factor. Our outcome variable babble is a continuous variable that presumably refers to some psychologically sensible measure of the extent to which someone is “babbling”. The details don’t really matter for our purpose. Take a look at the data in the jamovi spreadsheet view, as in Fig. 169.

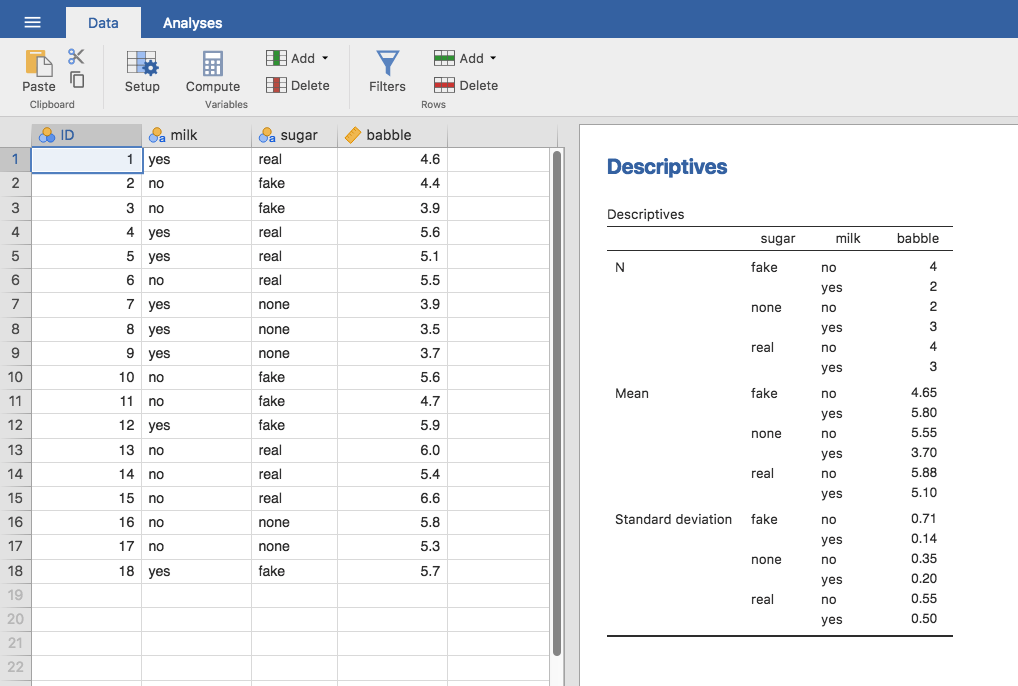
Fig. 169 The coffee data set in jamovi, showing descriptive statistics aggregated by the different levels of the factors sugar and milk

Looking at the table of means in Fig. 169 we get a strong impression that there are differences between the groups. This is especially true when we compare these means to the standard deviations for the babble variable. Across groups, this standard deviation varies from 0.14 to 0.71, which is fairly small relative to the differences in group means.[1] Whilst this at first may seem like a straightforward factorial ANOVA, a problem arises when we look at how many observations we have in each group. See the different Ns for different groups shown in Fig. 169. This violates one of our original assumptions, namely that the number of people in each group is the same. We haven’t really discussed how to handle this situation.

“Standard ANOVA” does not exist for unbalanced designs

Unbalanced designs lead us to the somewhat unsettling discovery that there isn’t really any one thing that we might refer to as a standard ANOVA. In fact, it turns out that there are three fundamentally different ways[2] in which you might want to run an ANOVA in an unbalanced design. If you have a balanced design all three versions produce identical results, with the sums of squares, F-values, etc., all conforming to the formulas that I gave at the start of the chapter. However, when your design is unbalanced they don’t give the same answers. Furthermore, they are not all equally appropriate to every situation. Some methods will be more appropriate to your situation than others. Given all this, it’s important to understand what the different types of ANOVA are and how they differ from one another.

The first kind of ANOVA is conventionally referred to as Type 1 sum of squares. I’m sure you can guess what the other two are called. The “sum of squares” part of the name was introduced by the SAS statistical software package and has become standard nomenclature, but it’s a bit misleading in some ways. I think the logic for referring to them as different types of sum of squares is that, when you look at the ANOVA tables that they produce, the key difference in the numbers is the SS values. The degrees of freedom don’t change, the MS values are still defined as SS divided by df, etc. However, what the terminology gets wrong is that it hides the reason why the SS values are different from one another. To that end, it’s a lot more helpful to think of the three different kinds of ANOVA as three different hypothesis testing strategies. These different strategies lead to different SS values, to be sure, but it’s the strategy that is the important thing here, not the SS values themselves. Recall from section ANOVA as a linear model, that any particular F-test is best thought of as a comparison between two linear models. So, when you’re looking at an ANOVA table, it helps to remember that each of those F-tests corresponds to a pair of models that are being compared. Of course, this leads naturally to the question of which pair of models is being compared. This is the fundamental difference between ANOVA Types 1, 2 and 3: each one corresponds to a different way of choosing the model pairs for the tests.

Type 1 sum of squares

The Type 1 method is sometimes referred to as the “sequential” sum of squares, because it involves a process of adding terms to the model one at a time. Consider, for instance, the coffee data. Suppose we want to run the full 3 × 2 factorial ANOVA, including interaction terms. The full model contains the outcome variable babble, the predictor variables sugar and milk, and the interaction term sugar * milk. This can be written as babble ~ sugar + milk + sugar * milk. The Type 1 strategy builds this model up sequentially, starting from the simplest possible model and gradually adding terms.

The simplest possible model for the data would be one in which neither milk nor sugar is assumed to have any effect on babbling. The only term that would be included in such a model is the intercept, written as babble ~ 1. This is our initial null hypothesis. The next simplest model for the data would be one in which only one of the two main effects is included. In the coffee data, there are two different possible choices here, because we could choose to add milk first or to add sugar first. The order actually turns out to matter, as we’ll see later, but for now let’s just make a choice arbitrarily and pick sugar. So, the second model in our sequence of models is babble ~ sugar, and it forms the alternative hypothesis for our first test. We now have our first hypothesis test:

Null model:	babble ~ 1
Alternative model:	babble ~ sugar

This comparison forms our hypothesis test of the main effect of sugar. The next step in our model building exercise is to add the other main effect term, so the next model in our sequence is babble ~ sugar + milk. The second hypothesis test is then formed by comparing the following pair of models:

Null model:	babble ~ sugar
Alternative model:	babble ~ sugar + milk

This comparison forms our hypothesis test of the main effect of milk. In one sense, this approach is very elegant: the alternative hypothesis from the first test forms the null hypothesis for the second one. It is in this sense that the Type 1 method is strictly sequential. Every test builds directly on the results of the last one. However, in another sense it’s very inelegant, because there’s a strong asymmetry between the two tests. The test of the main effect of sugar (the first test) completely ignores milk, whereas the test of the main effect of milk (the second test) does take sugar into account. In any case, the fourth model in our sequence is now the full model, babble ~ sugar + milk + sugar * milk, and the corresponding hypothesis test is:

Null model:	babble ~ sugar + milk
Alternative model:	babble ~ sugar + milk + sugar * milk

Type 3 sum of squares is the default hypothesis testing method used by jamovi ANOVA, so to run a Type 1 sum of squares analysis we have to select Type 1 in the Sum of squares selection box in the jamovi ANOVA → Model options. This gives us the ANOVA table shown in Fig. 170.

Fig. 170 ANOVA results table using Type 1 sum of squares in jamovi (with the coffee data set and a saturated model with the factors sugar, milk, and their interaction; factor sugar is entered first).

The big problem with using Type 1 sum of squares is the fact that it really does depend on the order in which you enter the variables. Yet, in many situations the researcher has no reason to prefer one ordering over another. This is presumably the case for our milk and sugar problem. Should we add milk first or sugar first? It feels exactly as arbitrary as a data analysis question as it does as a coffee-making question. There may in fact be some people with firm opinions about ordering, but it’s hard to imagine a principled answer to the question. Yet, look what happens when we change the ordering, as in Fig. 171.

Fig. 171 ANOVA results table using Type 1 sum of squares in jamovi (with the coffee data set and a saturated model with the factors milk, sugar, and their interaction; factor milk is entered first).

The p-values for both main effect terms have changed, and fairly dramatically. Among other things, the effect of milk has become significant (though one should avoid drawing any strong conclusions about this, as I’ve mentioned previously). Which of these two ANOVAs should one report? It’s not immediately obvious.

When you look at the hypothesis tests that are used to define the “first” main effect and the “second” one, it’s clear that they’re qualitatively different from one another. In our initial example, we saw that the test for the main effect of sugar completely ignores milk, whereas the test of the main effect of milk does take sugar into account. As such, the Type 1 testing strategy really does treat the first main effect as if it had a kind of theoretical primacy over the second one. In my experience there is very rarely if ever any theoretically primacy of this kind that would justify treating any two main effects asymmetrically.

The consequence of all this is that Type 1 tests are very rarely of much interest, and so we should move on to discuss Type 2 tests and Type 3 tests.

Type 3 sum of squares

Having just finished talking about Type 1 tests, you might think that the natural thing to do next would be to talk about Type 2 tests. However, I think it’s actually a bit more natural to discuss Type 3 tests (which are simple and the default in jamovi ANOVA) before talking about Type 2 tests (which are trickier). The basic idea behind Type 3 tests is extremely simple. Regardless of which term you’re trying to evaluate, run the F-test in which the alternative hypothesis corresponds to the full ANOVA model as specified by the user, and the null model just deletes that one term that you’re testing. For instance, in the example from the coffee data set, in which our full model was babble ~ sugar + milk + sugar * milk, the test for a main effect of sugar would correspond to a comparison between the following two models:

Null model:	babble ~ milk + sugar * milk
Alternative model:	babble ~ sugar + milk + sugar * milk

Similarly the main effect of milk is evaluated by testing the full model against a null model that removes the milk term, like so:

Null model:	babble ~ sugar + sugar * milk
Alternative model:	babble ~ sugar + milk + sugar * milk

Finally, the interaction term sugar * milk is evaluated in exactly the same way. Once again, we test the full model against a null model that removes the sugar * milk interaction term, like so:

Null model:	babble ~ sugar + milk
Alternative model:	babble ~ sugar + milk + sugar * milk

The basic idea generalises to higher order ANOVAs. For instance, suppose that we were trying to run an ANOVA with three factors, A, B and C, and we wanted to consider all possible main effects and all possible interactions, including the three way interaction A*B*C. The table below shows you what the Type 3 tests look like for this situation:

Term being tested is	Null model is outcome ~ …	Alternative model is outcome ~ …
A	B + C + A * B + A * C + B * C + A * B * C	A + B + C + A * B + A * C + B * C + A * B * C
B	A + C + A * B + A * C + B * C + A * B * C	A + B + C + A * B + A * C + B * C + A * B * C
C	A + B + A * B + A * C + B * C + A * B * C	A + B + C + A * B + A * C + B * C + A * B * C
A * B	A + B + C + A * C + B * C + A * B * C	A + B + C + A * B + A * C + B * C + A * B * C
A * C	A + B + C + A * B + B * C + A * B * C	A + B + C + A * B + A * C + B * C + A * B * C
B * C	A + B + C + A * B + A * C + A * B * C	A + B + C + A * B + A * C + B * C + A * B * C
A * B * C	A + B + C + A * B + A * C + B * C	A + B + C + A * B + A * C + B * C + A * B * C

As ugly as that table looks, it’s pretty simple. In all cases, the alternative hypothesis corresponds to the full model which contains three main effect terms (e.g. A), three two-way interactions (e.g. A * B) and one three-way interaction (i.e., A * B * C). The null model always contains 6 of these 7 terms, and the missing one is the one whose significance we’re trying to test.

At first pass, Type 3 tests seem like a nice idea. Firstly, we’ve removed the asymmetry that caused us to have problems when running Type 1 tests. And because we’re now treating all terms the same way, the results of the hypothesis tests do not depend on the order in which we specify them. This is definitely a good thing. However, there is a big problem when interpreting the results of the tests, especially for main effect terms. Consider the coffee data. Suppose it turns out that the main effect of milk is not significant according to the Type 3 tests. What this is telling us is that babble ~ sugar + sugar * milk is a better model for the data than the full model. But what does that even mean? If the interaction term sugar * milk was also non-significant, we’d be tempted to conclude that the data are telling us that the only thing that matters is sugar. But suppose we have a significant interaction term, but a non-significant main effect of milk. In this case, are we to assume that there really is an “effect of sugar”, an “interaction between milk and sugar”, but no “effect of milk”? That seems crazy. The right answer simply must be that it’s meaningless[3] to talk about the main effect if the interaction is significant. In general, this seems to be what most statisticians advise us to do, and I think that’s the right advice. But if it really is meaningless to talk about non-significant main effects in the presence of a significant interaction, then it’s not at all obvious why Type 3 tests should allow the null hypothesis to rely on a model that includes the interaction but omits one of the main effects that make it up. When characterised in this fashion, the null hypotheses really don’t make much sense at all.

Later on, we’ll see that Type 3 tests can be redeemed in some contexts, but first let’s take a look at the ANOVA results table using Type 3 sum of squares, see Fig. 172.

Fig. 172 ANOVA results table using Type 3 sum of squares in jamovi (with the coffee data set and a saturated model with the factors sugar, milk, and their interaction).

But be aware, one of the perverse features of the Type 3 testing strategy is that typically the results turn out to depend on the contrasts that you use to encode your factors (see section Different ways to specify contrasts if you’ve forgotten what the different types of contrasts are).[4]

Okay, so if the p-values that typically come out of Type 3 analyses (but not in jamovi) are so sensitive to the choice of contrasts, does that mean that Type 3 tests are essentially arbitrary and not to be trusted? To some extent that’s true, and when we turn to a discussion of Type 2 tests we’ll see that Type 2 analyses avoid this arbitrariness entirely, but I think that’s too strong a conclusion. Firstly, it’s important to recognise that some choices of contrasts will always produce the same answers (ah, so this is what is happening in jamovi). Of particular importance is the fact that if the columns of our contrast matrix are all constrained to sum to zero, then the Type 3 analysis will always give the same answers.

Type 2 sum of squares

Okay, so we’ve seen Type 1 and 3 tests now, and both are pretty straightforward. Type 1 tests are performed by gradually adding terms one at a time, whereas Type 3 tests are performed by taking the full model and looking to see what happens when you remove each term. However, both can have some limitations. Type 1 tests are dependent on the order in which you enter the terms, and Type 3 tests are dependent on how you code up your contrasts. Type 2 tests are a little harder to describe, but they avoid both of these problems, and as a result they are a little easier to interpret.

Type 2 tests are broadly similar to Type 3 tests. Start with a “full” model, and test a particular term by deleting it from that model. However, Type 2 tests are based on the marginality principle which states that you should not omit a lower order term from your model if there are any higher order ones that depend on it. So, for instance, if your model contains the two-way interaction A * B (a 2nd order term), then it really ought to contain the main effects A and B (1st order terms). Similarly, if it contains a three-way interaction term A * B * C, then the model must also include the main effects A, B and C as well as the simpler interactions A * B, A * C and B * C. Type 3 tests routinely violate the marginality principle. For instance, consider the test of the main effect of A in the context of a three-way ANOVA that includes all possible interaction terms. According to Type 3 tests, our null and alternative models are:

Null model:	outcome ~ B + C + A * B + A * C + B * C + A * B * C
Alternative model:	outcome ~ A + B + C + A * B + A * C + B*C + A * B * C

Notice that the null hypothesis omits A, but includes A * B, A * C and A * B * C as part of the model. This, according to the Type 2 tests, is not a good choice of null hypothesis. What we should do instead, if we want to test the null hypothesis that A is not relevant to our outcome, is to specify the null hypothesis that is the most complicated model that does not rely on A in any form, even as an interaction. The alternative hypothesis corresponds to this null model plus a main effect term of A. This is a lot closer to what most people would intuitively think of as a “main effect of A”, and it yields the following as our Type 2 test of the main effect of A:[5]

Null model:	outcome ~ B + C + B * C
Alternative model:	outcome ~ A + B + C + B * C

Anyway, just to give you a sense of how the Type 2 tests play out, here’s the full table of tests that would be applied in a three-way factorial ANOVA:

Term being tested is	Null model is outcome ~ …	Alternative model is outcome ~ …
A	B + C + B * C	A + B + C + B * C
B	A + C + A * C	A + B + C + A * C
C	A + B + A * B	A + B + C + A * B
A * B	A + A * C + B * C	A + B + C + A * B + A * C + B * C
A * C	A + B + C + A * B + B * C	A + B + C + A * B + A * C + B * C
B * C	A + B + C + A * B + A * C	A + B + C + A * B + A * C + B * C
A * B * C	A + B + C + A * B + A * C + B * C	A + B + C + A * B + A * C + B * C + A * B * C

In the context of the two way ANOVA that we’ve been using in the coffee data, the hypothesis tests are even simpler. The main effect of sugar corresponds to an F-test comparing these two models:

Null model:	babble ~ milk
Alternative model:	babble ~ sugar + milk

The test for the main effect of milk is

Null model:	babble ~ sugar
Alternative model:	babble ~ sugar + milk

Finally, the test for the interaction sugar * milk is:

Null model:	babble ~ sugar + milk
Alternative model:	babble ~ sugar + milk + sugar * milk

Running the tests are again straightforward. Just select Type 2 in the Sum of squares selection box in the jamovi ANOVA → Model options, This gives us the ANOVA table shown in Fig. 173.

Fig. 173 ANOVA results table using Type 2 sum of squares in jamovi (with the coffee data set and a saturated model with the factors sugar, milk, and their interaction).

Type 2 tests have some clear advantages over Type 1 and Type 3 tests. They don’t depend on the order in which you specify factors (unlike Type 1), and they don’t depend on the contrasts that you use to specify your factors (unlike Type 3). And although opinions may differ on this last point, and it will definitely depend on what you’re trying to do with your data, I do think that the hypothesis tests that they specify are more likely to correspond to something that you actually care about. As a consequence, I find that it’s usually easier to interpret the results of a Type 2 test than the results of a Type 1 or Type 3 test. For this reason my tentative advice is that, if you can’t think of any obvious model comparisons that directly map onto your research questions but you still want to run an ANOVA in an unbalanced design, Type 2 tests are probably a better choice than Type 1 or Type 3.[6]

Effect sizes (and non-additive sums of squares)

jamovi also provides the effect sizes η² and partial η² when you select these options, as in Fig. 173. However, when you’ve got an unbalanced design there’s a bit of extra complexity involved.

If you remember back to our very early discussions of ANOVA, one of the key ideas behind the sums of squares calculations is that if we add up all the SS terms associated with the effects in the model, and add that to the residual SS, they’re supposed to add up to the total sum of squares. And, on top of that, the whole idea behind η² is that, because you’re dividing one of the SS terms by the total SS value, an η² value can be interpreted as the proportion of variance accounted for by a particular term. But this is not so straightforward in unbalanced designs because some of the variance goes “missing”.

This seems a bit odd at first, but here’s why. When you have unbalanced designs your factors become correlated with one another, and it becomes difficult to tell the difference between the effect of Factor A and the effect of Factor B. In the extreme case, suppose that we’d run a 2 × 2 design in which the number of participants in each group had been as follows:

	sugar	no sugar
milk	100	0
no milk	0	100

Here we have a spectacularly unbalanced design: 100 people have milk and sugar, 100 people have no milk and no sugar, and that’s all. There are 0 people with milk and no sugar, and 0 people with sugar but no milk. Now suppose that, when we collected the data, it turned out there is a large (and statistically significant) difference between the “milk and sugar” group and the “no-milk and no-sugar” group. Is this a main effect of sugar? A main effect of milk? Or an interaction? It’s impossible to tell, because the presence of sugar has a perfect association with the presence of milk. Now suppose the design had been a little more balanced:

	sugar	no sugar
milk	100	5
no milk	5	100

This time around, it’s technically possible to distinguish between the effect of milk and the effect of sugar, because we have a few people that have one but not the other. However, it will still be pretty difficult to do so, because the association between sugar and milk is still extremely strong, and there are so few observations in two of the groups. Again, we’re very likely to be in the situation where we know that the predictor variables (milk and sugar) are related to the outcome (babbling), but we don’t know if the nature of that relationship is a main effect of one or the other predictor, or the interaction.

This uncertainty is the reason for the missing variance. The “missing” variance corresponds to variation in the outcome variable that is clearly attributable to the predictors, but we don’t know which of the effects in the model is responsible. When you calculate Type 1 sum of squares, no variance ever goes missing. The sequential nature of Type 1 sum of squares means that the ANOVA automatically attributes this variance to whichever effects are entered first. However, the Type 2 and Type 3 tests are more conservative. Variance that cannot be clearly attributed to a specific effect doesn’t get attributed to any of them, and it goes missing.

---

[1]	This discrepancy in standard deviations might (and should) make you wonder if we have a violation of the homogeneity of variance assumption. I’ll leave it as an exercise for the reader to double check this using the Levene test option.

[2]

Actually, this is a bit of a lie. ANOVAs can vary in other ways besides the ones I’ve discussed in this book. For instance, I’ve completely ignored the difference between fixed-effect models in which the levels of a factor are “fixed” by the experimenter or the world, and random-effect models in which the levels are random samples from a larger population of possible levels (this book only covers fixed-effect models). Don’t make the mistake of thinking that this book, or any other one, will tell you “everything you need to know” about statistics, any more than a single book could possibly tell you everything you need to know about psychology, physics or philosophy. Life is too complicated for that to ever be true. This isn’t a cause for despair, though. Most researchers get by with a basic working knowledge of ANOVA that doesn’t go any further than this book does. I just want you to keep in mind that this book is only the beginning of a very long story, not the whole story.

[3]	Or, at the very least, rarely of interest.

[4]	However, in jamovi the results for Type 3 sum of squares ANOVA are the same regardless of the contrast selected, so jamovi is obviously doing something different!

[5]

Note, of course, that this does depend on the model that the user specified. If the original ANOVA model doesn’t contain an interaction term for B * C, then obviously it won’t appear in either the null or the alternative. But that’s true for Types 1, 2 and 3. They never include any terms that you didn’t include, but they make different choices about how to construct tests for the ones that you did include.

[6]

I find it amusing to note that the default in R is Type 1 and the default in SPSS and jamovi is Type 3. Neither of these appeals to me all that much. Relatedly, I find it depressing that almost nobody in the psychological literature ever bothers to report which Type of tests they ran, much less the order of variables (for Type 1) or the contrasts used (for Type 3). Often they don’t report what software they used either. The only way I can ever make any sense of what people typically report is to try to guess from auxiliary cues which software they were using, and to assume that they never changed the default settings. Please don’t do this! Now that you know about these issues make sure you indicate what software you used, and if you’re reporting ANOVA results for unbalanced data, then specify what Type of tests you ran, specify order information if you’ve done Type 1 tests and specify contrasts if you’ve done Type 3 tests. Or, even better, do hypotheses tests that correspond to things you really care about and then report those!