Section author: Danielle J. Navarro and David R. Foxcroft
ANOVA as a linear model¶
One of the most important things to understand about ANOVA and regression is that they’re basically the same thing. On the surface of it, you maybe wouldn’t think this is true. After all, the way that I’ve described them so far suggests that ANOVA is primarily concerned with testing for group differences, and regression is primarily concerned with understanding the correlations between variables. And, as far as it goes that’s perfectly true. But when you look under the hood, so to speak, the underlying mechanics of ANOVA and regression are awfully similar. In fact, if you think about it, you’ve already seen evidence of this. ANOVA and regression both rely heavily on sums of squares (SS), both make use of F-tests, and so on. Looking back, it’s hard to escape the feeling that chapters Correlation and linear regression and Comparing several means (one-way ANOVA) were a bit repetitive.
The reason for this is that ANOVA and regression are both kinds of linear models. In the case of regression, this is kind of obvious. The regression equation that we use to define the relationship between predictors and outcomes is the equation for a straight line, so it’s quite obviously a linear model, with the equation
where Yp is the outcome value for the p-th observation (e.g., p-th person), X1p is the value of the first predictor for the p-th observation, X2p is the value of the second predictor for the p-th observation, the b0, b1, and b2 terms are our regression coefficients, and ϵp is the p-th residual. If we ignore the residuals ϵp and just focus on the regression line itself, we get the following formula:
where Ŷp is the value of Y that the regression line predicts for person p, as opposed to the actually-observed value Yp. The thing that isn’t immediately obvious is that we can write ANOVA as a linear model as well. However, it’s actually pretty straightforward to do this. Let’s start with a really simple example, rewriting a 2 × 2 factorial ANOVA as a linear model.
Some data¶
To make things concrete, let’s suppose that our outcome variable is the
grade that a student receives in my class, a ratio-scale variable
corresponding to a mark from 0% to 100%. There are two predictor
variables of interest: whether or not the student turned up to lectures
(the attend variable) and whether or not the student actually read
the textbook (the reading variable). We’ll say that attend = 1
if the student attended class, and attend = 0 if they did not.
Similarly, we’ll say that reading = 1 if the student read the
textbook, and reading = 0 if they did not.
Okay, so far that’s simple enough. The next thing we need to do is to
wrap some maths around this (sorry!). For the purposes of this example,
let Yp denote the grade of the p-th student in the
class. This is not quite the same notation that we used earlier in this
chapter. Previously, we’ve used the notation Yrci to refer to
the i-th person in the r-th group for predictor 1 (the
row factor) and the c-th group for predictor 2 (the column
factor). This extended notation was really handy for describing how the
SS values are calculated, but it’s a pain in the current context, so
I’ll switch notation here. Now, the Yp notation is visually
simpler than Yrci, but it has the shortcoming that it doesn’t
actually keep track of the group memberships! That is, if I told you
that Y0,0,3 = 35, you’d immediately know that we’re talking
about a student (the 3rd such student, in fact) who didn’t attend the
lectures (i.e., attend = 0) and didn’t read the textbook (i.e.
reading = 0), and who ended up failing the class (grade = 35).
But if I tell you that Yp = 35, all you know is that the
p-th student didn’t get a good grade. We’ve lost some key
information here. Of course, it doesn’t take a lot of thought to figure
out how to fix this. What we’ll do instead is introduce two new
variables X1p and X2p that keep track of this
information. In the case of our hypothetical student, we know that
X1p = 0 (i.e., attend = 0) and X2p = 0 (i.e.,
reading = 0). So the data might look like this:
| person, p | grade, Yp | attendance, X1p | reading, X2p |
|---|---|---|---|
| 1 | 90 | 1 | 1 |
| 2 | 87 | 1 | 1 |
| 3 | 75 | 0 | 1 |
| 4 | 60 | 1 | 0 |
| 5 | 35 | 0 | 0 |
| 6 | 50 | 0 | 0 |
| 7 | 65 | 1 | 0 |
| 8 | 70 | 0 | 1 |
This isn’t anything particularly special, of course. It’s exactly the format in
which we expect to see our data! See the rtfm data set. We can use the
jamovi analysis Descriptives to confirm that this data set corresponds to a
balanced design, with 2 observations for each combination of attend and
reading. In the same way we can also calculate the mean grade for each
combination. This is shown in Fig. 159. Looking at the
mean scores, one gets the strong impression that reading the text and attending
the class both matter a lot.
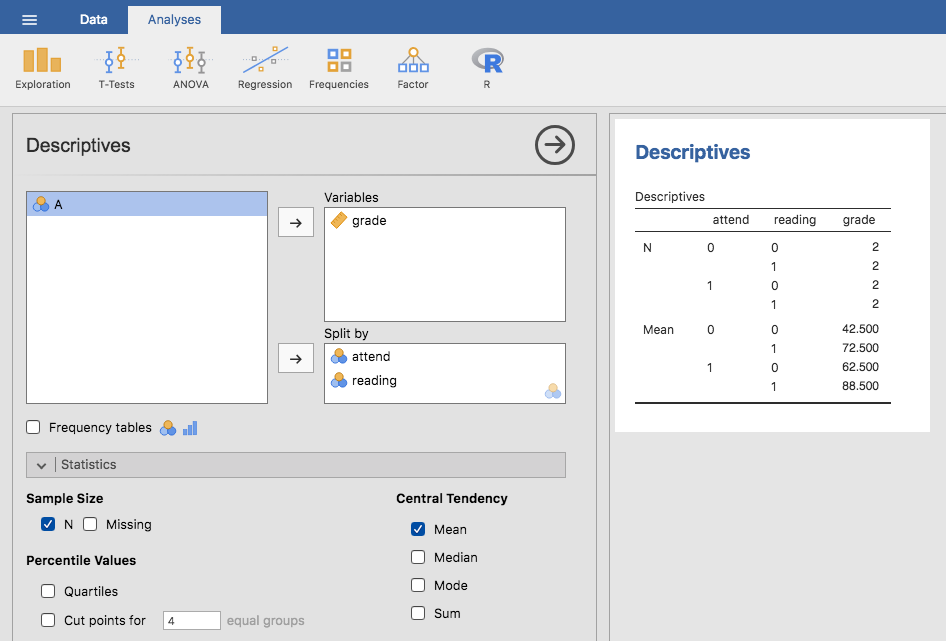
Fig. 159 jamovi descriptives for the rtfm dataset
ANOVA with binary factors as a regression model¶
Okay, let’s get back to talking about the mathematics. We now have our data expressed in terms of three numeric variables: the continuous variable Y and the two binary variables X1 and X2. What I want you to recognise is that our 2 × 2 factorial ANOVA is exactly equivalent to the regression model:
This is, of course, the exact same equation that I used earlier to describe a
two-predictor regression model! The only difference is that X1 and
X2 are now binary variables (i.e., values can only be 0 or 1),
whereas in a regression analysis we expect that X1 and X2
will be continuous. There’s a couple of ways I could try to convince you of
this. One possibility would be to do a lengthy mathematical exercise proving
that the two are identical. However, I’m going to go out on a limb and guess
that most of the readership of this book will find that annoying rather than
helpful. Instead, I’ll explain the basic ideas and then rely on jamovi to show
that ANOVA analyses and regression analyses aren’t just similar, they’re
identical for all intents and purposes. Let’s start by running this as an
ANOVA. To do this, we’ll use the rtfm data set, and
Fig. 160 shows what we get when we run the analysis in
jamovi.
Fig. 160 ANOVA of the rtfm data set in jamovi: Model with two factors attend
and reading but without the interaction term for these two factors
So, by reading the key numbers off the ANOVA table and the mean scores that we presented earlier, we can see that the students obtained a higher grade if they attended class (F(1,5) = 21.6, p = 0.0056) and if they read the textbook: F(1,5) = 52.3,*p* = 0.0008. Let’s make a note of those p-values and those F-statistics.
Now let’s think about the same analysis from a linear regression perspective.
In the rtfm data set, we have encoded attend and reading as if they
were numeric predictors. In this case, this is perfectly acceptable. There
really is a sense in which a student who turns up to class (i.e.
attend = 1) has in fact done “more attendance” than a student who does not
(i.e. attend = 0). So it’s not at all unreasonable to include it as a
predictor in a regression model. It’s a little unusual, because the predictor
only takes on two possible values, but it doesn’t violate any of the
assumptions of linear regression. And it’s easy to interpret. If the regression
coefficient for attend is greater than 0 it means that students that attend
lectures get higher grades. If it’s less than zero then students attending
lectures get lower grades. The same is true for our reading variable.
Wait a second though. Why is this true? It’s something that is intuitively
obvious to everyone who has taken a few stats classes and is comfortable with
the maths, but it isn’t clear to everyone else at first pass. To see why this
is true, it helps to look closely at a few specific students. Let’s start by
considering the 6th and 7th students in our data set (i.e. p = 6 and p = 7).
Neither one has read the textbook, so in both cases we can set reading = 0.
Or, to say the same thing in our mathematical notation, we observe
X2,6 = 0 and X2,7 = 0. However, student number 7 did turn
up to lectures (i.e., attend = 1, X1,7 = 1) whereas student
number 6 did not (i.e., attend = 0, X1,6 = 0). Now let’s look at
what happens when we insert these numbers into the general formula for our
regression line. For student number 6, the regression predicts that:
So we’re expecting that this student will obtain a grade corresponding to the value of the intercept term b0. What about student 7? This time when we insert the numbers into the formula for the regression line, we obtain the following:
Because this student attended class, the predicted grade is equal to the
intercept term b0 plus the coefficient associated with the
attend variable, b1. So, if b1 is greater than zero,
we’re expecting that the students who turn up to lectures will get higher
grades than those students who don’t. If this coefficient is negative we’re
expecting the opposite: students who turn up at class end up performing much
worse. In fact, we can push this a little bit further. What about student
number 1, who turned up to class (X1,1 = 1) and read the textbook
(X2,1 = 1)? If we plug these numbers into the regression we get:
So if we assume that attending class helps you get a good grade (i.e., b1 > 0) and if we assume that reading the textbook also helps you get a good grade (i.e., b2 > 0), then our expectation is that student 1 will get a grade that that is higher than student 6 and student 7.
And at this point you won’t be at all suprised to learn that the regression model predicts that student 3, who read the book but didn’t attend lectures, will obtain a grade of b2 + b0. I won’t bore you with yet another regression formula. Instead, what I’ll do is show you the following table of expected grades:
| read the textbook? | |||
|---|---|---|---|
| no | yes | ||
| attended? | no | b0 | b0 + b2 |
| yes | b0 + b1 | b0 + b1 + b2 | |
As you can see, the intercept term b0 acts like a kind of “baseline” grade that you would expect from those students who don’t take the time to attend class or read the textbook. Similarly, b1 represents the boost that you’re expected to get if you come to class, and b2 represents the boost that comes from reading the textbook. In fact, if this were an ANOVA you might very well want to characterise b1 as the main effect of attendance, and b2 as the main effect of reading! In fact, for a simple 2 × 2 ANOVA that’s exactly how it plays out.
Okay, now that we’re really starting to see why ANOVA and regression are
basically the same thing, let’s actually run our regression using the rtfm
data set and the jamovi regression analysis to convince ourselves that this is
really true. Running the regression in the usual way gives the results shown in
Fig. 161.
Fig. 161 Regression analysis for the rtfm data set in jamovi: Model with two
factors attend and reading but without the interaction term for
these two factors
There’s a few interesting things to note here. First, notice that the intercept term is 43.5 which is close to the “group” mean of 42.5 observed for those two students who didn’t read the text or attend class. Second, notice that we have the regression coefficient of b1 = 18.0 for the attendance variable, suggesting that those students that attended class scored 18% higher than those who didn’t. So our expectation would be that those students who turned up to class but didn’t read the textbook would obtain a grade of b0 + b1, which is equal to 43.5 + 18.0 = 61.5. You can verify for yourself that the same thing happens when we look at the students that read the textbook.
Actually, we can push a little further in establishing the equivalence of our
ANOVA and our regression. Look at the p-values associated with the attend
variable and the reading variable in the regression output. They’re
identical to the ones we encountered earlier when running the ANOVA. This might
seem a little surprising, since the test used when running our regression model
calculates a t-statistic and the ANOVA calculates an F-statistic. However,
if you can remember all the way back to chapter
Introduction to probability, I mentioned that there’s a relationship
between the t-distribution and the F-distribution. If you have some
quantity that is distributed according to a t-distribution with k degrees of
freedom and you square it, then this new squared quantity follows an
F-distribution whose degrees of freedom are 1 and k. We can check this with
respect to the t-statistics in our regression model. For the attend
variable we get a t-value of 4.65. If we square this number we end up
with 21.6, which matches the corresponding F-statistic in our ANOVA.
Finally, one last thing you should know. Because jamovi understands the fact
that ANOVA and regression are both examples of linear models, it lets you
extract the classic ANOVA table from your regression model using the Linear
Regression - Model Coefficients - Omnibus Test - ANOVA test, and
this will give you the table shown in Fig. 162.
Fig. 162 Results table showing the Omnibus ANOVA Test from the jamovi regression
analysis using the rtfm dataset
How to encode non binary factors as contrasts¶
At this point, I’ve shown you how we can view a 2 × 2 ANOVA into a linear
model. And it’s pretty easy to see how this generalises to a 2 × 2 × 2 ANOVA or
a 2 × 2 × 2 × 2 ANOVA. It’s the same thing, really. You just add a new binary
variable for each of your factors. Where it begins to get trickier is when we
consider factors that have more than two levels. Consider, for instance, the 3
× 2 ANOVA that we ran earlier in this chapter using the clinicaltrial data
set. How can we convert the three-level drug factor into a
numerical form that is appropriate for a regression?
The answer to this question is pretty simple, actually. All we have to do is
realise that a three-level factor can be redescribed as two binary variables.
Suppose, for instance, I were to create a new binary variable called
druganxifree. Whenever the drug variable is equal to anxifree we
set druganxifree = 1. Otherwise, we set druganxifree = 0. This variable
sets up a contrast, in this case between anxifree and the other two
drugs. By itself, of course, the druganxifree contrast isn’t enough to
fully capture all of the information in our drug variable. We need a second
contrast, one that allows us to distinguish between joyzepam and the
placebo. To do this, we can create a second binary contrast, called
drugjoyzepam, which equals 1 if the drug is joyzepam and 0 if it is
not. Taken together, these two contrasts allows us to perfectly discriminate
between all three possible levels of drug. The table below illustrates
this:
drug |
druganxifree |
drugjoyzepam |
placebo |
0 | 0 |
anxifree |
1 | 0 |
joyzepam |
0 | 1 |
If the drug administered to a patient is a placebo then both of the
two contrast variables will equal 0. If the drug is anxifree then the
druganxifree variable will equal 1, and drugjoyzepam will be 0. The
reverse is true for joyzepam: drugjoyzepam is 1 and druganxifree
is 0.
Creating contrast variables is not too difficult to do using the jamovi
Compute command to create a new variable. For example, to create the
druganxifree variable, write this logical expression in the formula box:
IF(drug == 'anxifree', 1, 0). Similarly, to create the new variable
drugjoyzepam use this logical expression:
IF(drug == 'joyzepam', 1, 0). Likewise for CBTtherapy:
IF(therapy == 'CBT', 1, 0). You can see these new variables, and the
corresponding logical expressions, in the clinicaltrial2 data set.
We have now recoded our three-level factor in terms of two binary variables, and we’ve already seen that ANOVA and regression behave the same way for binary variables. However, there are some additional complexities that arise in this case, which we’ll discuss in the next section.
The equivalence between ANOVA and regression for non-binary factors¶
Now we have two different versions of the same data set. Our original data in
which the drug variable from the clinicaltrial data set is expressed as
a single three-level factor, and the clinicaltrial2 data set in which it is
expanded into two binary contrasts. Once again, the thing that we want to
demonstrate is that our original 3 × 2 factorial ANOVA is equivalent to a
regression model applied to the contrast variables. Let’s start by re-running
the ANOVA, with results shown in Fig. 163.
Fig. 163 jamovi ANOVA results for the clinicaltrial dataset: Unsaturated model
with the two main effects for drug and therapy but without an
interaction component for these two factors
Obviously, there are no surprises here. That’s the exact same ANOVA that we ran
earlier. Next, let’s run a regression using druganxifree, drugjoyzepam
and CBTtherapy as the predictors. The results are shown in
Fig. 164.
Fig. 164 jamovi regression results for the clinicaltrial data set: Model with the
generated contrast variables druganxifree and drugjoyzepam
Hmm. This isn’t the same output that we got last time. Not surprisingly, the
regression output prints out the results for each of the three predictors
separately, just like it did every other time we conducted a regression
analysis. On the one hand we can see that the p-value for the CBTtherapy
variable is exactly the same as the one for the therapy factor in
our original ANOVA, so we can be reassured that the regression model is doing
the same thing as the ANOVA did. On the other hand, this regression model is
testing the
druganxifree contrast and the drugjoyzepam contrast
separately, as if they were two completely unrelated variables. It’s not
surprising of course, because the poor regression analysis has no way of
knowing that drugjoyzepam and druganxifree are actually the two
different contrasts that we used to encode our three-level drug factor. As
far as it knows, drugjoyzepam and druganxifree are no more related to
one another than drugjoyzepam and therapyCBT. However, you and I know
better. At this stage we’re not at all interested in determining whether these
two contrasts are individually significant. We just want to know if there’s an
“overall” effect of drug. That is, what we want jamovi to do is to run
some kind of “model comparison” test, one in which the two “drug-related”
contrasts are lumped together for the purpose of the test. Sound familiar? All
we need to do is specify our null model, which in this case would include the
CBTtherapy predictor, and omit both of the drug-related variables, as in
Fig. 165.
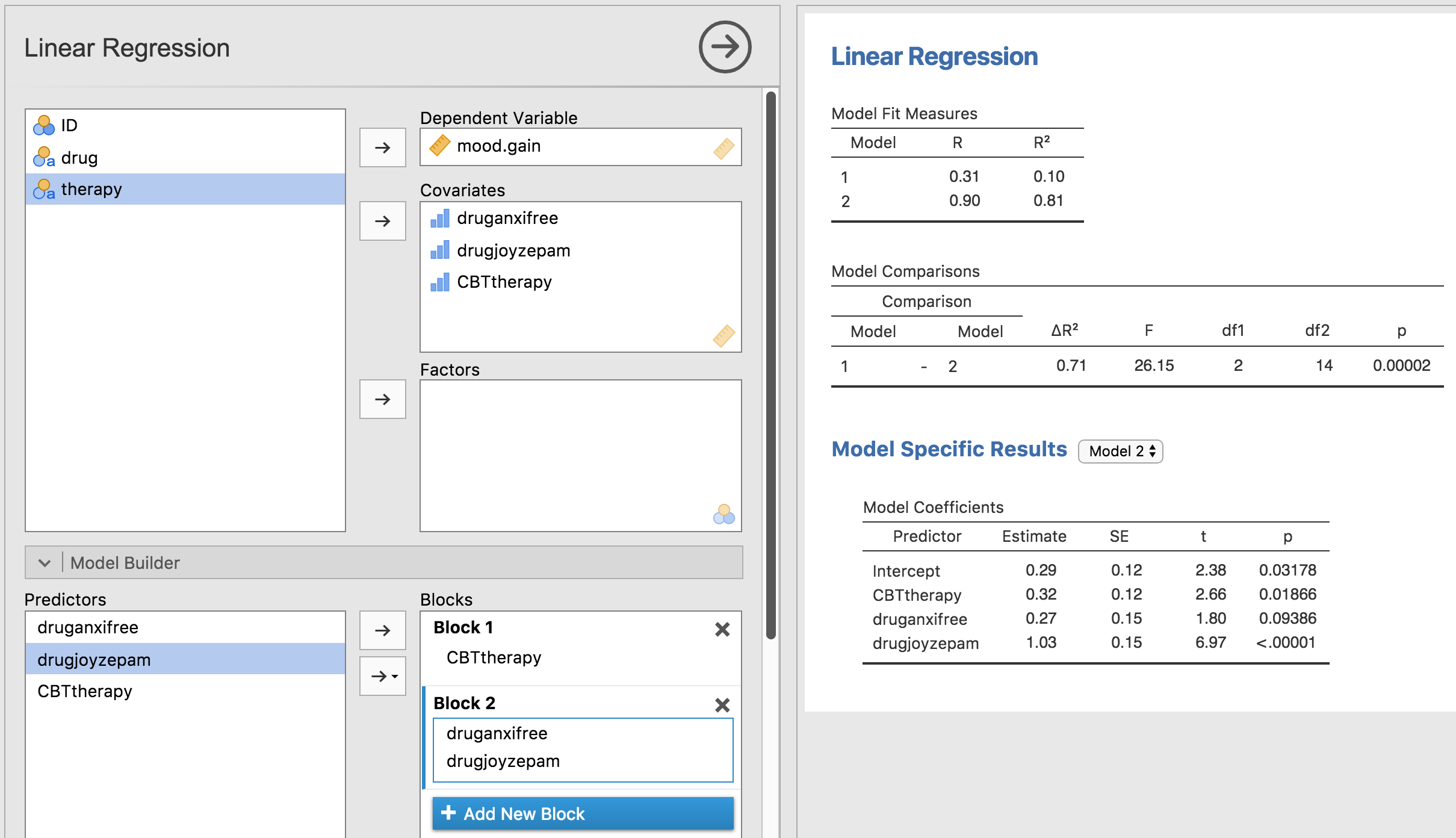
Fig. 165 Model comparison in jamovi regression: Null model (Model 1) vs. model using the generated contrast variables (Model 2)
Ah, that’s better. Our F-statistic is 26.15, the degrees of freedom are 2 and
14, and the p-value is 0.00002. The numbers are identical to the ones we
obtained for the main effect of drug in our original ANOVA. Once again we
see that ANOVA and regression are essentially the same. They are both linear
models, and the underlying statistical machinery for ANOVA is identical to the
machinery used in regression. The importance of this fact should not be
understated. Throughout the rest of this chapter we’re going to rely heavily on
this idea.
Although we went through all the faff of computing new variables in jamovi for
the contrasts druganxifree and drugjoyzepam, just to show that ANOVA
and regression are essentially the same, in the jamovi linear regression
analysis there is actually a nifty shortcut to get these contrasts, see
Fig. 166. What jamovi is doing here is allowing you to enter
the predictor variables that are factors as, wait for it… factors! Smart, eh.
You can also specify which group to use as the reference level, via the
Reference Levels option. We’ve changed this to placebo and
no.therapy, respectively, because this makes most sense.
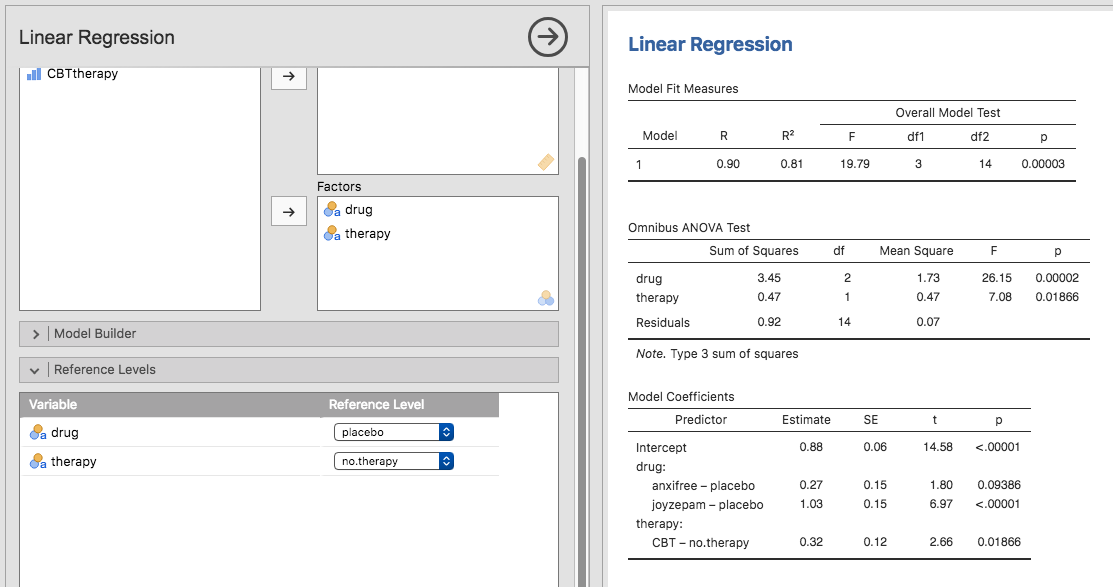
Fig. 166 Regression analysis with factors and contrasts in jamovi, including omnibus ANOVA test results
If you also click on the ANOVA test checkbox under the Model
Coefficients → Omnibus Test option, we see that the F-statistic is
26.15, the degrees of freedom are 2 and 14, and the p-value is 0.00002 (see
Fig. 166). The numbers are identical to the ones we obtained
for the main effect of drug in our original ANOVA. Once again, we see that
ANOVA and regression are essentially the same. They are both linear models, and
the underlying statistical machinery for ANOVA is identical to the machinery
used in regression.
Degrees of freedom as parameter counting!¶
At long last, I can finally give a definition of degrees of freedom that
I am happy with. Degrees of freedom are defined in terms of the number
of parameters that have to be estimated in a model. For a regression
model or an ANOVA, the number of parameters corresponds to the number of
regression coefficients (i.e. b-values), including the
intercept. Keeping in mind that any F-test is always a
comparison between two models and the first df is the difference
in the number of parameters. For example, in the model comparison above,
the null model (mood.gain ~ therapyCBT) has two parameters: there’s
one regression coefficient for the therapyCBT variable, and a second
one for the intercept. The alternative model
(mood.gain ~ druganxifree + drugjoyzepam + therapyCBT) has four
parameters: one regression coefficient for each of the three contrasts,
and one more for the intercept. So the degrees of freedom associated
with the difference between these two models is df1 = 4 - 2 = 2.
What about the case when there doesn’t seem to be a null model? For
instance, you might be thinking of the F-test that shows up when
you select F Test under the Linear Regression - Model
Fit options. I originally described that as a test of the regression
model as a whole. However, that is still a comparison between two
models. The null model is the trivial model that only includes 1
regression coefficient, for the intercept term. The alternative model
contains K + 1 regression coefficients, one for each of the K
predictor variables and one more for the intercept. So the
df-value that you see in this F-test is equal to
df1 = K + 1 - 1 = K.
What about the second df-value that appears in the F-test? This always refers to the degrees of freedom associated with the residuals. It is possible to think of this in terms of parameters too, but in a slightly counter-intuitive way. Think of it like this. Suppose that the total number of observations across the study as a whole is N. If you wanted to perfectly describe each of these N values, you need to do so using, well… N numbers. When you build a regression model, what you’re really doing is specifying that some of the numbers need to perfectly describe the data. If your model has K predictors and an intercept, then you’ve specified K + 1 numbers. So, without bothering to figure out exactly how this would be done, how many more numbers do you think are going to be needed to transform a K + 1 parameter regression model into a perfect re-description of the raw data? If you found yourself thinking that (K + 1) + (N - K - 1) = N, and so the answer would have to be N - K - 1, well done! That’s exactly right. In principle you can imagine an absurdly complicated regression model that includes a parameter for every single data point, and it would of course provide a perfect description of the data. This model would contain N parameters in total, but we’re interested in the difference between the number of parameters required to describe this full model (i.e. N) and the number of parameters used by the simpler regression model that you’re actually interested in (i.e., K + 1), and so the second degrees of freedom in the F-test is df2 = N - K - 1, where K is the number of predictors (in a regression model) or the number of contrasts (in an ANOVA). In the example I gave above, there are N = 18 observations in the data set and K + 1 = 4 regression coefficients associated with the ANOVA model, so the degrees of freedom for the residuals is df2 = 18 - 4 = 14.