Section author: Danielle J. Navarro and David R. Foxcroft
Assumptions of the one-way ANOVA¶
Like any statistical test, analysis of variance relies on some assumptions about the data, specifically the residuals. There are three key assumptions that you need to be aware of: normality, homogeneity of variance and independence.
If you remember back to subsection The model for the data and the meaning of *F* which I hope you at least skimmed even if you didn’t read the whole thing, I described the statistical models underpinning ANOVA in this way:
In these equations µ refers to a single grand population mean which is the same for all groups, and µk is the population mean for the k-th group. Up to this point we’ve been mostly interested in whether our data are best described in terms of a single grand mean (the null hypothesis) or in terms of different group-specific means (the alternative hypothesis). This makes sense, of course, as that’s actually the important research question! However, all of our testing procedures have, implicitly, relied on a specific assumption about the residuals, ϵik, namely that
ϵik ~ Normal(0, σ²)
None of the maths works properly without this bit. Or, to be precise, you can still do all the calculations and you’ll end up with an F-statistic, but you have no guarantee that this F-statistic actually measures what you think it’s measuring, and so any conclusions that you might draw on the basis of the F test might be wrong.
So, how do we check whether the assumption about the residuals is accurate? Well, as I indicated above, there are three distinct claims buried in this one statement, and we’ll consider them separately.
- Homogeneity of variance. Notice that we’ve only got the one value for the population standard deviation (i.e., σ), rather than allowing each group to have it’s own value (i.e., σk). This is referred to as the homogeneity of variance (sometimes called homoscedasticity) assumption. ANOVA assumes that the population standard deviation is the same for all groups. We’ll talk about this extensively in subsection Checking the homogeneity of variance assumption.
- Normality. The residuals are assumed to be normally distributed. As we saw in subsection Checking the normality of a sample, we can assess this by looking at QQ-plots (or running a Shapiro-Wilk test). I’ll talk about this more in an ANOVA context in subsection Checking the normality assumption.
- Independence. The independence assumption is a little trickier. What it basically means is that, knowing one residual tells you nothing about any other residual. All of the ϵik values are assumed to have been generated without any “regard for” or “relationship to” any of the other ones. There’s not an obvious or simple way to test for this, but there are some situations that are clear violations of this. For instance, if you have a repeated-measures design, where each participant in your study appears in more than one condition, then independence doesn’t hold. There’s a special relationship between some observations, namely those that correspond to the same person! When that happens, you need to use something like repeated measures ANOVA (see section Repeated measures one-way ANOVA).
Checking the homogeneity of variance assumption¶
There’s more than one way to skin a cat, as the saying goes, and more than one way to test the homogeneity of variance assumption, too (though for some reason no-one made a saying out of that). The most commonly used test for this that I’ve seen in the literature is the Levene test (Levene, 1960), and the closely related Brown-Forsythe test (Brown & Forsythe, 1974).
Regardless of whether you’re doing the standard Levene test or the Brown-Forsythe test, the test statistic, which is sometimes denoted F but also sometimes written as W, is calculated in exactly the same way that the F-statistic for the regular ANOVA is calculated, just using a Zik rather than Yik. With that in mind, we can go on to look at how to run the test in jamovi.
The Levene test is shockingly simple. Suppose we have our outcome variable Yik. All we do is define a new variable, which I’ll call Zik, corresponding to the absolute deviation from the group mean
Okay, what good does this do us? Well, let’s take a moment to think about what Zik actually is and what we’re trying to test. The value of Zik is a measure of how the i-th observation in the k-th group deviates from its group mean. And our null hypothesis is that all groups have the same variance, i.e., the same overall deviations from the group means! So the null hypothesis in a Levene test is that the population means of Z are identical for all groups. Hmm. So what we need now is a statistical test of the null hypothesis that all group means are identical. Where have we seen that before? Oh right, that’s what ANOVA is, and so all that the Levene test does is run an ANOVA on the new variable Zik.
What about the Brown-Forsythe test? Does that do anything particularly different? Nope. The only change from the Levene test is that it constructs the transformed variable Z in a slightly different way, using deviations from the group medians rather than deviations from the group means. That is, for the Brown-Forsythe test
where mediank(Y) is the median for group k.
Running the Levene-test in jamovi¶
Okay, so how do we run the Levene test? Simple really - under the ANOVA →
Assumption Checks option, just click on the Homogeneity tests
checkbox. If we look at the output, shown in Fig. 134, we see that
the test is non-significant (F{2,15} = 1.45, p = 0.266), so it looks like
the homogeneity of variance assumption is fine. However, looks can be
deceptive! If your sample size is pretty big, then the Levene test could show
up a significant effect (i.e., p < 0.05) even when the homogeneity of
variance assumption is not violated to an extent which troubles the
robustness of ANOVA. This was the point George Box was making in the
quote above. Similarly, if your sample size is quite small, then the
homogeneity of variance assumption might not be satisfied and yet a
Levene test could be non-significant (i.e. p > 0.05). What this
means is that, alongside any statistical test of the assumption being
met, you should always plot the standard deviation around the means for
each group / category in the analysis… just to see if they look fairly
similar (i.e. homogeneity of variance) or not.

Fig. 134 Levene test output for One-Way ANOVA in jamovi
Removing the homogeneity of variance assumption¶
In our example, the homogeneity of variance assumption turned out to be a
pretty safe one: the Levene test came back non-significant (notwithstanding
that we should also look at the plot of standard deviations), so we probably
don’t need to worry. However, in real life we aren’t always that lucky. How do
we save our ANOVA when the homogeneity of variance assumption is violated? If
you recall from our discussion of t-tests, we’ve seen this problem before.
The Student t-test assumes equal variances, so the solution was to use the
Welch t-test, which does not. In fact, Welch (1951) also
showed how we can solve this problem for ANOVA too (the Welch One-way
test). It’s implemented in jamovi using the One-Way ANOVA analysis. This
is a specific analysis approach just for one-way ANOVA, and to run the Welch
one-way ANOVA for our example, we would re-run the analysis as previously, but
this time use the jamovi ANOVA → One Way ANOVA analysis command, and
check the option Don't assume equal (Welch’s) (see Fig. 135).
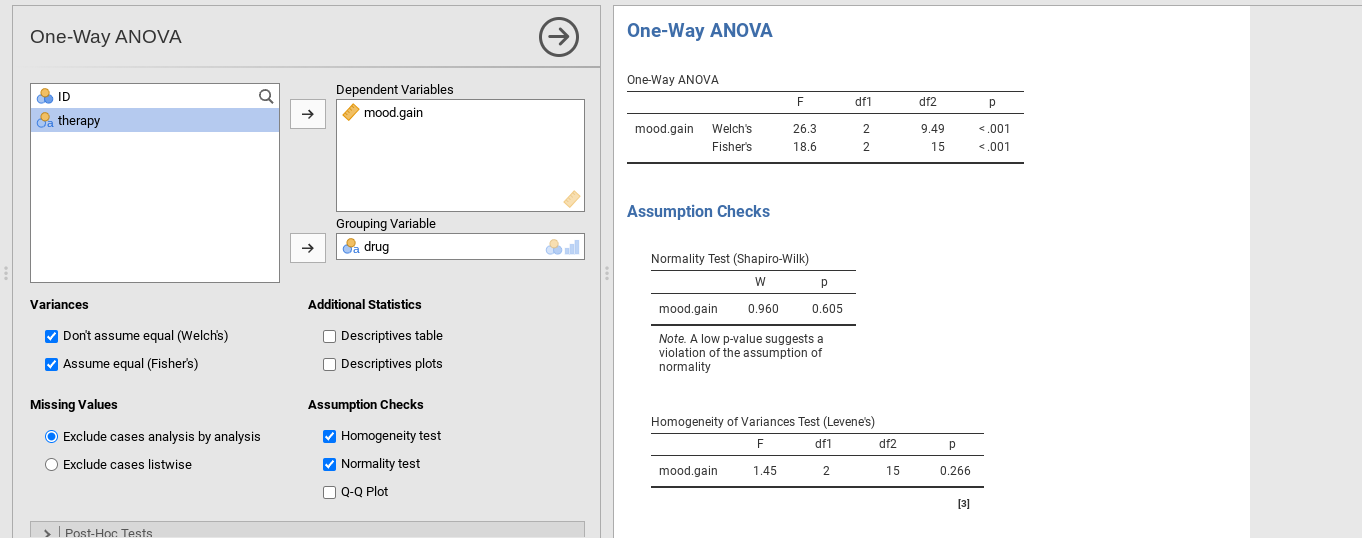
Fig. 135 Welch’s test as part of the One-Way ANOVA analysis in jamovi
To understand what’s happening here, let’s compare these numbers with those
obtained earlier in section Running an ANOVA in jamovi, namely: F(2,15) = 18.611,
p = 0.00009. As shown in Fig. 135, these values are also
displayed in the One-Way ANOVA table (in the row starting with
Fisher's) if the option Assume equal (Fisher's) was chosen.
Okay, so originally our ANOVA gave us the result F(2,15) = 18.6, whereas the Welch one-way test gave us F(2,9.49) = 26.32. In other words, the Welch test has reduced the within-groups degrees of freedom from 15 to 9.49, and the F-value has increased from 18.6 to 26.32.
Checking the normality assumption¶
Testing the normality assumption is relatively straightforward. We covered most of what you need to know in section Checking the normality of a sample. The only thing we really need to do is draw a QQ plot and, in addition if it is available, run the Shapiro-Wilk test. The QQ plot is shown in Fig. 136 and it looks pretty normal to me. If the Shapiro-Wilk test is not significant (i.e. p > 0.05) then this indicates that the assumption of normality is not violated. However, as with Levene’s test, if the sample size is large then a significant Shapiro-Wilk test may in fact be a false positive, where the assumption of normality is not violated in any substantive problematic sense for the analysis. And, similarly, a very small sample can produce false negatives. That’s why a visual inspection of the QQ plot is important.
Alongside inspecting the QQ plot for any deviations from normality, the Shapiro-Wilk test for our data does show a non-significant effect, with p = 0.6053 (see Fig. 135). This therefore supports the QQ plot assessment; both checks find no indication that normality is violated.
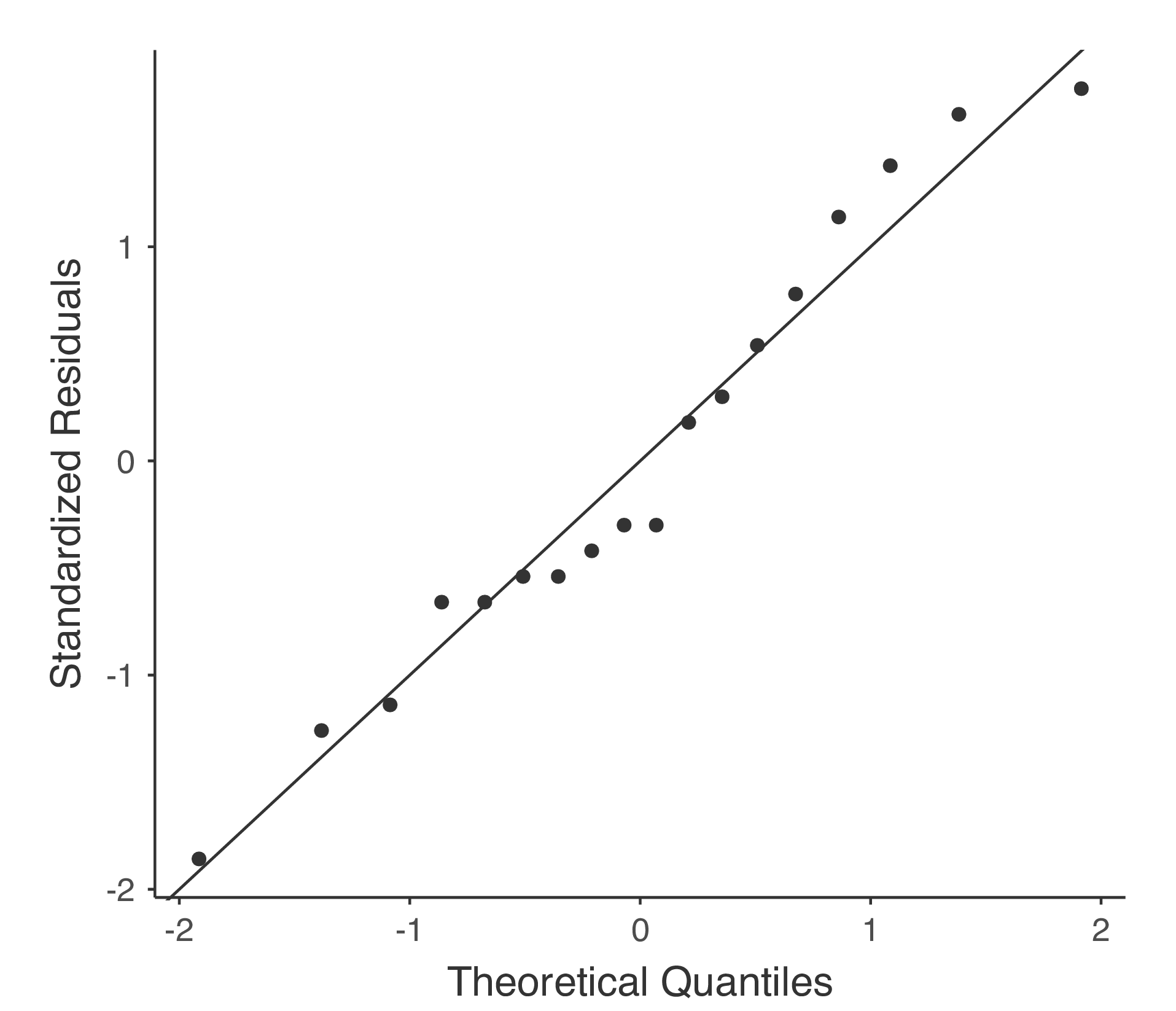
Fig. 136 QQ-plot produced from jamovi One-Way ANOVA options
Removing the normality assumption¶
Now that we’ve seen how to check for normality, we are led naturally to ask what we can do to address violations of normality. In the context of a One-way ANOVA, the easiest solution is probably to switch to a non-parametric test (i.e., one that doesn’t rely on any particular assumption about the kind of distribution involved). We’ve seen non-parametric tests before, in section Testing non-normal data with Wilcoxon tests. When you only have two groups, the Mann-Whitney or the Wilcoxon test provides the non-parametric alternative that you need. When you’ve got three or more groups, you can use the Kruskal-Wallis rank sum test (Kruskal & Wallis, 1952). So that’s the test we’ll talk about next.
The Kruskal-Wallis test is surprisingly similar to ANOVA, in some ways. In ANOVA we started with Yik, the value of the outcome variable for the i-th person in the k-th group. For the Kruskal-Wallis test what we’ll do is rank order all of these Yik values and conduct our analysis on the ranked data.
So let’s let Rik refer to the ranking given to the i-th member of the k-th group. Now, let’s calculate R̄k, the average rank given to observations in the k-th group:
and let’s also calculate R̄, the grand mean rank
Now that we’ve done this, we can calculate the squared deviations from the grand mean rank R̄. When we do this for the individual scores, i.e., if we calculate (Rik – R̄)², what we have is a “nonparametric” measure of how far the ik-th observation deviates from the grand mean rank. When we calculate the squared deviation of the group means from the grand means, i.e., if we calculate (R̄k – R̄)², then what we have is a nonparametric measure of how much the group deviates from the grand mean rank. With this in mind, we’ll follow the same logic that we did with ANOVA and define our ranked sums of squares measures, much like we did earlier. First, we have our “total ranked sums of squares”
and we can define the “between groups ranked sums of squares” like this
So, if the null hypothesis is true and there are no true group differences at all, you’d expect the between group rank sums RSSb to be very small, much smaller than the total rank sums RSStot. Qualitatively this is very much the same as what we found when we went about constructing the ANOVA F-statistic, but for technical reasons the Kruskal-Wallis test statistic, usually denoted K, is constructed in a slightly different way,
and if the null hypothesis is true, then the sampling distribution of K is approximately χ² with G - 1 degrees of freedom (where G is the number of groups). The larger the value of K, the less consistent the data are with the null hypothesis, so this is a one-sided test. We reject H0 when K is sufficiently large.
The description in the previous section illustrates the logic behind the Kruskal-Wallis test. At a conceptual level, this is the right way to think about how the test works. However, from a purely mathematical perspective it’s needlessly complicated. I won’t show you the derivation, but you can use a bit of algebraic jiggery-pokery [1] to show that the equation for K can be rewritten as
It’s this last equation that you sometimes see given for K. This is way easier to calculate than the version I described in the previous section, but it’s just that it’s totally meaningless to actual humans. It’s probably best to think of K the way I described it earlier, as an analogue of ANOVA based on ranks. But keep in mind that the test statistic that gets calculated ends up with a rather different look to it than the one we used for our original ANOVA.
But wait, there’s more! Dear lord, why is there always more? The story
I’ve told so far is only actually true when there are no ties in the raw
data. That is, if there are no two observations that have exactly the
same value. If there are ties, then we have to introduce a correction
factor to these calculations. At this point I’m assuming that even the
most diligent reader has stopped caring (or at least formed the opinion
that the tie-correction factor is something that doesn’t require their
immediate attention). So I’ll very quickly tell you how it’s calculated,
and omit the tedious details about why it’s done this way. Suppose we
construct a frequency table for the raw data, and let fj be the
number of observations that have the j-th unique value. This
might sound a bit abstract, so here’s a concrete example from the
frequency table of mood.gain from the clinicaltrial data set:
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.8 | 0.9 | 1.1 | 1.2 | 1.3 | 1.4 | 1.7 | 1.8 |
| 1 | 1 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 2 | 2 | 1 | 1 |
Looking at this table, notice that the third entry in the frequency
table has a value of 2. Since this corresponds to a
mood.gain of 0.3, this table is telling us that two people’s mood
increased by 0.3. More to the point, in the mathematical notation I
introduced above, this is telling us that f3 = 2. Yay. So, now
that we know this, the tie correction factor (TCF) is:
The tie-corrected value of the Kruskal-Wallis statistic is obtained by dividing the value of K by this quantity. It is this tie-corrected version that jamovi calculates. And at long last, we’re actually finished with the theory of the Kruskal-Wallis test. I’m sure you’re all terribly relieved that I’ve cured you of the existential anxiety that naturally arises when you realise that you don’t know how to calculate the tie-correction factor for the Kruskal-Wallis test. Right?
How to run the Kruskal-Wallis test in jamovi¶
Despite the horror that we’ve gone through in trying to understand what the
Kruskal-Wallis test actually does, it turns out that running the test is pretty
painless, since jamovi has an analysis as part of the ANOVA analysis set called
Non-Parametric - One-Way ANOVA (Kruskall-Wallis). Most of the time
you’ll have data like the clinicaltrial data set, in which you have your
outcome variable mood.gain and a grouping variable drug. If so, you can
just go ahead and run the analysis in jamovi. What this gives us is a
Kruskal-Wallis χ² = 12.076, df = 2, p-value = 0.00239, as in
Fig. 137.
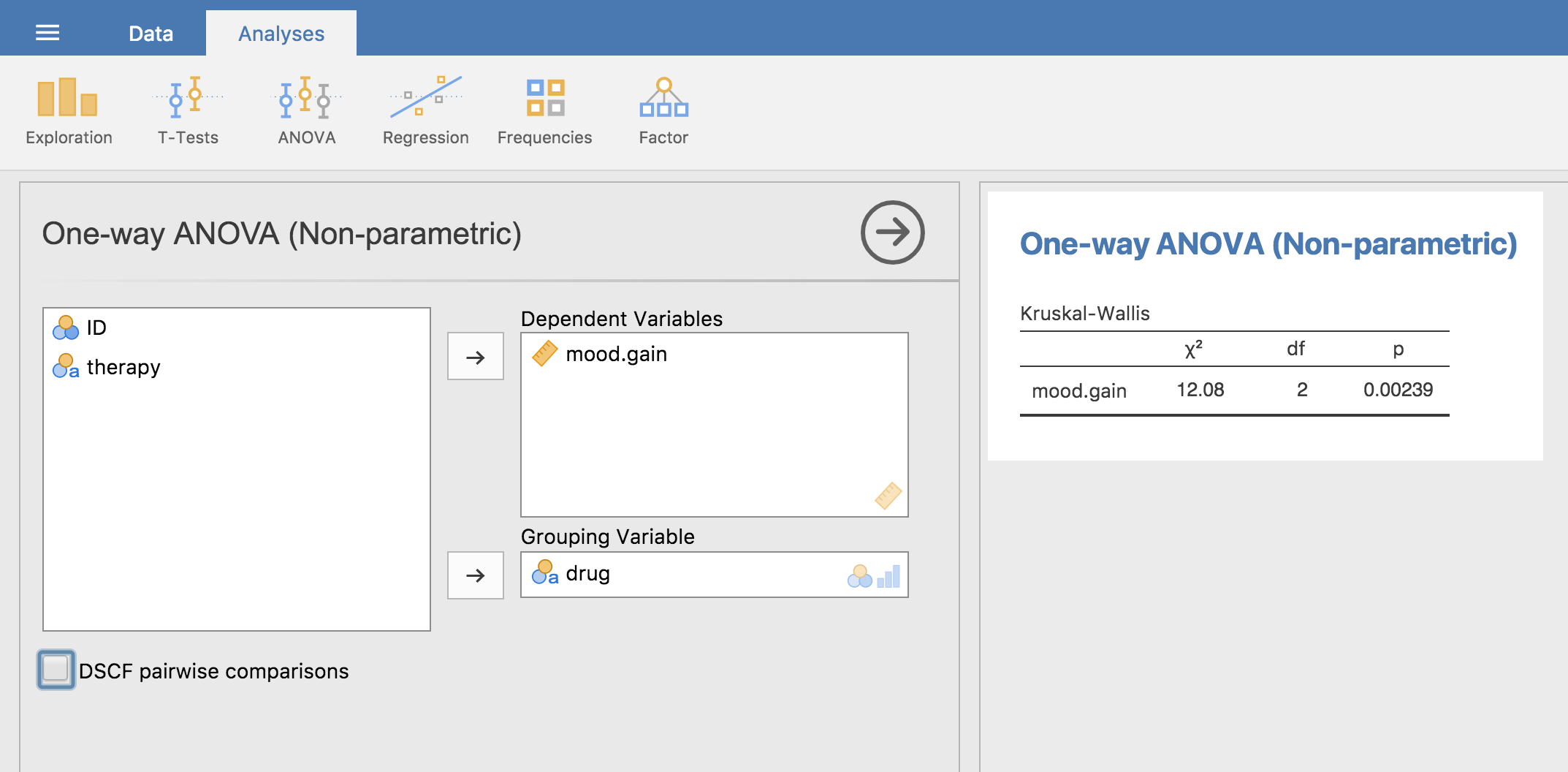
Fig. 137 Non-parametric One-Way ANOVA (Kruskal-Wallis) in jamovi
| [1] | A technical term. |