Section author: Danielle J. Navarro and David R. Foxcroft
The law of large numbers¶
In the previous section I showed you the results of one fictitious IQ experiment with a sample size of N = 100. The results were somewhat encouraging as the true population mean is 100 and the sample mean of 98.5 is a pretty reasonable approximation to it. In many scientific studies that level of precision is perfectly acceptable, but in other situations you need to be a lot more precise. If we want our sample statistics to be much closer to the population parameters, what can we do about it?
The obvious answer is to collect more data. Suppose that we ran a much
larger experiment, this time measuring the IQs of 10,000 people. We can
simulate the results of this experiment using jamovi. The IQsim data
set is a jamovi data file. In this file I have generated 10,000 random
numbers sampled from a normal distribution for a population with
mean = 100 and sd = 15. This was done by computing a new
variable using the = NORM(100,15) function. A histogram and density
plot shows that this larger sample is a much better approximation to the
true population distribution than the smaller one. This is reflected in
the sample statistics. The mean IQ for the larger sample turns out to be
99.68 and the standard deviation is 14.90. These values are now very
close to the true population, as Fig. 59 demonstrates.
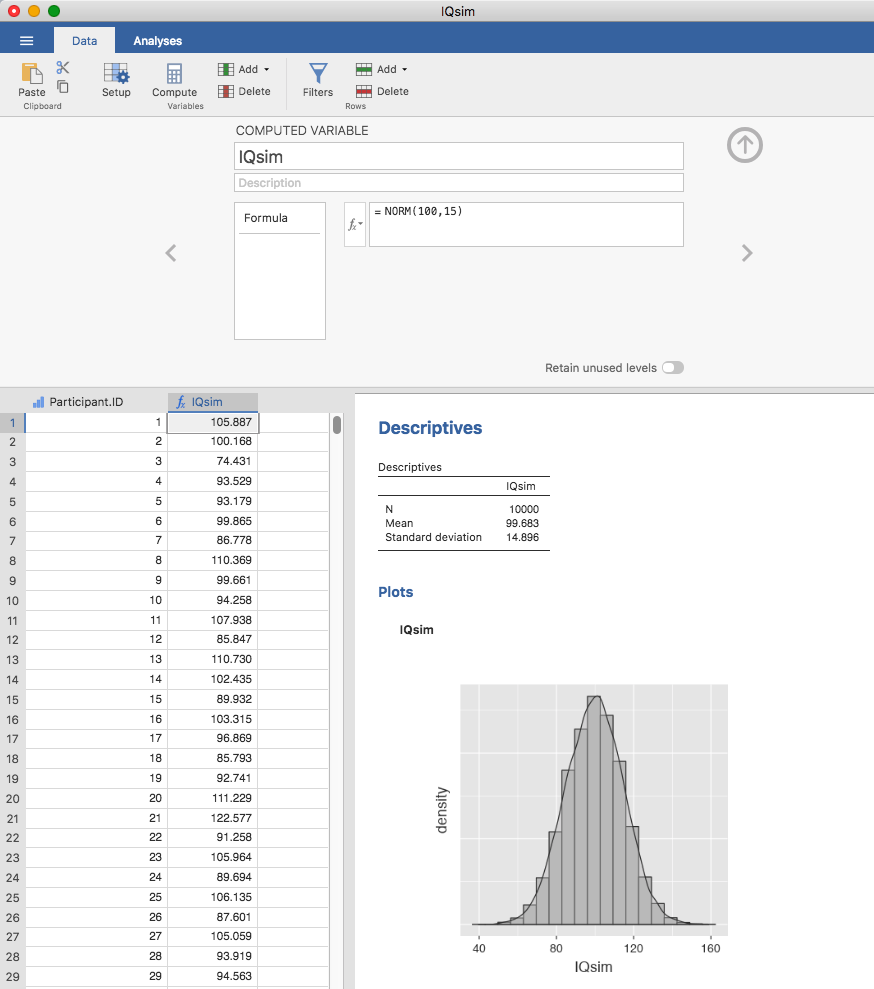
Fig. 59 Random sample drawn from a normal distribution using jamovi
I feel a bit silly saying this, but the thing I want you to take away from this is that large samples generally give you better information. I feel silly saying it because it’s so bloody obvious that it shouldn’t need to be said. In fact, it’s such an obvious point that when Jacob Bernoulli, one of the founders of probability theory, formalised this idea back in 1713 he was kind of a jerk about it. Here’s how he described the fact that we all share this intuition:
For even the most stupid of men, by some instinct of nature, by himself and without any instruction (which is a remarkable thing), is convinced that the more observations have been made, the less danger there is of wandering from one’s goal (Stigler, 1986).
Okay, so the passage comes across as a bit condescending (not to mention sexist), but his main point is correct. It really does feel obvious that more data will give you better answers. The question is, why is this so? Not surprisingly, this intuition that we all share turns out to be correct, and statisticians refer to it as the law of large numbers. The law of large numbers is a mathematical law that applies to many different sample statistics but the simplest way to think about it is as a law about averages. The sample mean is the most obvious example of a statistic that relies on averaging (because that’s what the mean is… an average), so let’s look at that. When applied to the sample mean what the law of large numbers states is that as the sample gets larger, the sample mean tends to get closer to the true population mean. Or, to say it a little bit more precisely, as the sample size “approaches” infinity (written as N → ∞), the sample mean approaches the population mean (X̄ → µ).[1]
I don’t intend to subject you to a proof that the law of large numbers is true, but it’s one of the most important tools for statistical theory. The law of large numbers is the thing we can use to justify our belief that collecting more and more data will eventually lead us to the truth. For any particular data set the sample statistics that we calculate from it will be wrong, but the law of large numbers tells us that if we keep collecting more data those sample statistics will tend to get closer and closer to the true population parameters.
| [1] | Technically, the law of large numbers pertains to any sample statistic that can be described as an average of independent quantities. That’s certainly true for the sample mean. However, it’s also possible to write many other sample statistics as averages of one form or another. The variance of a sample, for instance, can be rewritten as a kind of average and so is subject to the law of large numbers. The minimum value of a sample, however, cannot be written as an average of anything and is therefore not governed by the law of large numbers. |